培養學生化歸思想的教學案例設計

曹辰

[摘 要] 數學新課標明確指出，數學思想是數學知識和方法在更高層次上的抽象和概括. 在教學中，如果能從數學思想的高度去規劃、設計教學過程，會明顯提升學生對數學的認識. 本文通過在教學中對問題進行梯次設置，將復雜問題轉化為熟悉問題的方式，培養學生的化歸思想，進而提高學生解決數學問題的能力.

[關鍵詞] 化歸思想；問題轉化；教學案例

研究背景

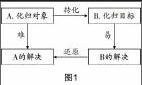
《義務教育數學課程標準（2011版）》明確指出：“數學思想蘊涵在數學知識形成、發展和應用的過程中，是數學知識和方法在更高層次上的抽象與概括.”作為數學思想方法的典型代表，化歸思想方法已成為一種普遍運用的思想方法，不僅在數學家的研究工作中，在中學數學教師的教學實踐中也得到了廣泛的重視和運用. 新的數學基礎教育課程改革把思想方法的重要性提到了前所未有的高度. 張奠宙教授認為“所謂化歸方法，就是將一個問題A進行變形，使其歸結為另一已解決的問題B，既然B已解決，那么A也就解決了”，其轉化過程如圖1所示.

在中學學習階段培養學生的化歸思想，對于學生更深、更透徹地理解數學，有著不可替代的作用. 如果能夠在日常教學中設計一些專題訓練，通過梯度設置問題，就能更好地整合內容，引導學生發現問題之間的聯系，進而培養學生的化歸能力.

研究設計

為了更好地向學生展示化歸思想在數學學習中的應用，本研究將旋轉問題與尺規作圖進行結合，設計了3道系列問題（如表1）. 問題1的設計意圖是在一個簡單的數學情景中，讓學生回憶用尺規畫等邊三角形的方法，做化歸之前的準備工作；問題2的設計意圖是要求學生具備一定的推理能力，希望學生經過對已知條件進行推理和分析后，將問題2轉化成問題1的情景；問題3的設計意圖是，希望學生解決前兩問后，經過推理和分析，將此問題轉化成前兩問的問題情景，最終達到此問題的解決.

筆者的教學目的在于通過尺規作圖培養學生在幾何學習中的化歸思想. 每道題均包含等邊三角形的尺規作圖，但通過對等邊三角形頂點位置的限制，每道題的難度逐步上升. 希望學生在思考問題的過程中，發現新問題與原有情景之間的聯系，并將新問題進行轉化.

研究過程？搖

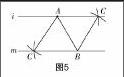
在課堂中，筆者首先提出問題1. 在選取點B后，所有學生均回憶起了等邊三角形的尺規作圖，非常順利地完成了作圖，如圖5.

完成問題1后，所有學生均回憶起了等邊三角形尺規作圖的畫法，達到了問題1的設置意圖. 說明全班學生對于課標中要求的尺規作圖知識有了很好的掌握. 在此基礎上，為進一步考查學生的化歸思想，筆者提出了問題2.

筆者給了全班學生5分鐘的嘗試時間，60%的學生順利地完成了作圖. 在課后訪談中，筆者選取了3位成功解決問題的學生與2位未能解決問題的學生，聽取了他們的思考過程. 5位學生均表示，他們發現該問題無法像問題1一樣直接確定點B的位置，進而作出等邊三角形. 但成功解決該問題的3位學生又表示，既然點B會出現在直線i上，只要等邊三角形ABC存在，∠BAC=60°是始終不變的，因此只需要確保∠BAC=60°，即可在直線m上確定點C，再與點A結合，利用第一問的方法作出等邊三角形，即可確定點B的位置.

在所有成功解決問題的學生中，均出現了類似圖6的作圖痕跡. 這說明學生已經把問題2中相對復雜的問題情景，轉化成問題1中已經解決過的熟悉問題，進而完成了問題2. 在完成了∠BAC=60°的作圖后，點C既在射線AC上，又在直線m上，所以點C為這兩條線的交點. 確定了點C的位置之后，可以完成等邊三角形ABC的作圖，如圖7（問題2完全解決）.

這道題較高的完成度，說明大部分學生對于等邊三角形邊、角性質已經具備較強的轉化能力，其化歸流程符合張奠宙教授的表述，如圖8.

在問題3中，題目對等邊三角形三個頂點的位置作出更加苛刻的限制，全班學生嘗試的思路各異，均不太理想，沒有人成功解決. 學生的典型嘗試作答結果如表2.

既然沒有學生成功解決問題3，說明該問題的設置已經超出了學生現有的認知水平，導致學生無法將問題3直接轉化成前面已經解決的問題. 為此，筆者將問題1、問題2組合在了一起，提出了問題2.5，希望通過條件與結論的提示，讓學生在解決該問后，可以成功解決問題3（如表3）.

同時，因為點B是直線m上任意一點，隨著點B在直線m上運動，其對應點C會始終處于直線BC上，說明頂點C的運動軌跡即為直線BC. 因此，完成等邊三角形ACB的作圖，即問題2的作圖后，就可以直接確定頂點C的運動軌跡. 此時，全班共有50%的學生完成了三點共線的證明，意識到點C的運動軌跡為一條直線，完成了從問題2.5到問題2的轉化.

最后，筆者帶領學生重新審視之前未解決的問題3.

根據問題2.5的探究結論，根據點A與直線m的位置，可以直接作出點C的運動軌跡，即圖13中新出現的直線. 再結合原題，會發現問題3中的點C既會出現在直線n上，又會出現在軌跡直線BC上，因此，符合題意的等邊三角形頂點C會出現在軌跡直線BC與直線n的交點處.

確定了點C的位置后，線段AC即為等邊三角形的邊長，最終得到符合題目要求的等邊三角形ABC . 在問題2.5闡述清楚并進行嚴格證明后，全班有80%的同學將問題3進行了成功轉化，完成了之前無法解決的問題.

在問題3的教學過程中，轉化流程比從問題2到問題1的轉化流程要復雜一些，如圖14. 其中，問題2.5的設置對于問題3的解決具有決定性作用.

研究反思

1. 教學過程

結合課堂教學效果過程，筆者意識到需要嚴格基于學生的能力對問題進行梯度設置. 在最初設計中，問題2與問題3之間的跨度太大，導致沒有任何一個學生在問題3中可以產生有價值的結論. 隨著問題2.5的添加，學生對問題3的接受程度會有明顯的提高. 在幾何的學習過程中，經常需要利用化歸思想，將問題進行轉化. 在問題2中，在無法確定邊長的情況下，轉而去研究角度性質；在問題3中，既然無法在直線n上確定點C的位置，轉而去研究等邊三角形頂點C的運動軌跡，這種將復雜問題進行轉化的思路在學習數學、研究數學的過程中經常使用.

2. 教學理念

通過本節課的教學設計，筆者發現如果通過對練習進行梯次設置，引導學生將新的問題轉化為已經解決的問題，將會明顯提高學生對于不熟悉問題的接受、理解程度. 學生在學習數學的基本知識時，首先要在教師的啟發下先對化歸思想產生感性認識，進而在反復理解、使用的基礎上達到理性認識. 重視和加強化歸思想的教育過程中，教師的作用至關重要. 中學數學教師不僅要有扎實的數學功底，還應有較好的化歸思想方法素養，才可以將數學知識和數學思想方法有機地聯系起來，帶領學生更好地理解數學，欣賞數學. 在學習數學的過程中，只有始終從數學思想方法的高度去理解數學，才能更好地解決數學問題，提高數學素養，培養數學能力.