偏心受壓冷彎薄壁槽鋼的卷邊角度優化設計

吳夢景　黃栩浩　張旭　朱玨　趙銀海

摘要：為了使得鋼結構的性能與用鋼量比達到最優，前人對槽型鋼的截面尺寸優化進行了較為充分的研究。但是，涉及卷邊角度的優化特別是偏心受壓工況下的優化分析卻很缺乏。以Yao-Teng偏心受壓計算公式，結合遺傳算法，以冷彎卷邊槽鋼柱偏心受壓為例，將槽鋼卷邊角度與偏心距作為設計變量，尋找在不同偏心距受壓情況下，達到最大畸變屈曲臨界應力的卷邊角度。基于有限條分析程序，對兩端簡支與兩端固支情況下不同截面尺寸構件的畸變屈曲臨界應力進行了計算分析，最終得出不同偏心距受壓下統一的最優卷邊角度。為了方便工程設計人員設計時參考，建議卷邊角度統一取為100°。

關鍵詞：偏心受壓；斜卷邊槽鋼；有限條；遺傳算法；最優卷邊角度

中圖分類號：TU391

文獻標志碼：A

文章編號：1674-4764（2016）06-0091-06

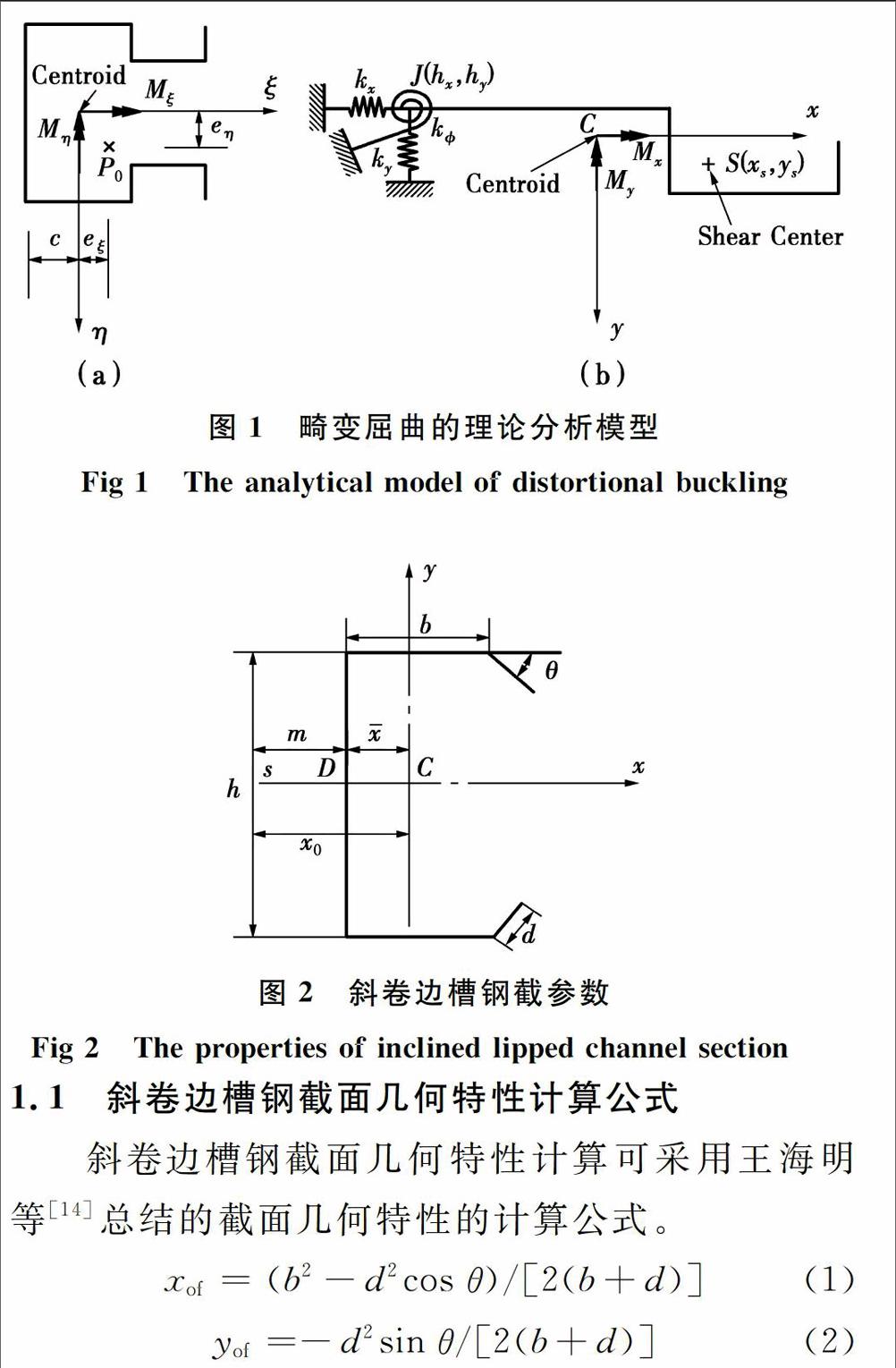
隨著生產技術的不斷更新發展，冷彎成型鋼構件朝著高強度、薄壁、截面形式復雜的趨勢發展，出現了幾種常見的屈曲模式，分別為：局部屈曲、畸變屈曲和整體屈曲。由于可以用加勁及加支撐的方式來提高構件的局部屈曲和整體屈曲的臨界應力，畸變屈曲則很可能成為最終主導構件失效的屈曲模式。Lau和Hancock等提出了簡化模型，推導出了受壓構件彈性畸變屈曲臨界應力。學者Li等考慮翼緣板件彎曲的影響，在Lau和Hancock的畸變屈曲模型基礎上進行修正，并推導出了類似于Lau和Hancock公式的彈性畸變屈曲臨界應力計算公式。其公式可計算卷邊槽形、Z形以及∑形冷彎薄壁型鋼構件的畸變屈曲應力。周緒紅等考慮腹板屈曲對彈簧剛度的影響并提出了折減系數，推導兩端簡支、固支卷邊槽鋼畸變屈曲臨界應力計算公式。Song等采用了半解析有限條法對槽鋼截面受剪力荷載進行分析。楊娜等通過有限元與試驗相對比，研究了組合效應對冷彎C型鋼構件滯回性能的改善作用。Teng等采用如圖1所示的近似模型，推導出雙向偏心受壓構件卷邊槽鋼彈性畸變屈曲荷載的穩定方程，并提出了單向偏壓和純彎載荷畸變屈曲計算公式并對其公式進行相應的簡化。研究表明，改變卷邊與翼緣的夾角（后簡稱卷邊角度）θ（如圖2）不僅會改變斜卷邊槽鋼的截面幾何特性，還會改變卷邊對翼緣的約束作用，從而導致斜卷邊槽鋼構件發生畸變屈曲時臨界應力以及畸變屈曲承載力發生變化。在此基礎上，通過改變卷邊的角度，從而達到提高構件承載力的目的，這為工程優化與改變構件截面形式來提高構件的強度與剛度提供了新的思路。

遺傳算法是一種常見的全局優化的概率算法，采用遺傳算法對工程問題進行優化，搜索過程既不受優化函數連續性的約束，也沒有優化函數必須可導的要求，同時可進行對目標優化設計。也避免了給定初始值要求，能夠有效地進行全局搜索。本文將姚諫等口胡（簡稱Yao-Teng）推導得到的卷邊槽鋼畸變屈曲臨界應力簡化計算公式編成相應的程序，再利用遺傳算法對其卷邊角度進行優

1.Yao-Tellg卷邊槽鋼畸變屈曲應力計算公式

采用Yao-Teng卷邊槽鋼畸變屈曲臨界應力計算過程中，需要的斜卷邊槽鋼截面幾何特性可采用王春剛，張耀春計算研究得到的以卷邊角度為變量的截面幾何特性的計算公式。

斜卷邊槽鋼截面幾何特性計算簡圖如圖2所示：腹板高度為h，翼緣寬度為b，卷邊長度為d，厚度為t，θ為卷邊角度；以截面的形心軸定義為z軸和y軸；點C和點S分別為截面的形心和剪心；D為腹板中點。

2.冷彎卷邊槽鋼角度優化模型

2.1優化的目標文件及函數

將Yao-Teng編成計算槽鋼偏心受壓畸變屈曲臨界應力目標函數文件。以槽鋼的偏心受壓畸變屈曲臨界應力作為目標函數P=-mainσcrd。

2.2變量及變量的約束條件

以卷邊角度θ和偏心距e為變量，卷邊角度取值范圍為30°到160°。則約束條件為30°<θ<160°，偏心距e則針對不同截面分別取10、20、30、40mm。

3.卷邊槽鋼畸變屈曲臨界應力計算及優化結果分析

3.1斜卷邊槽鋼屈曲應力計算結果

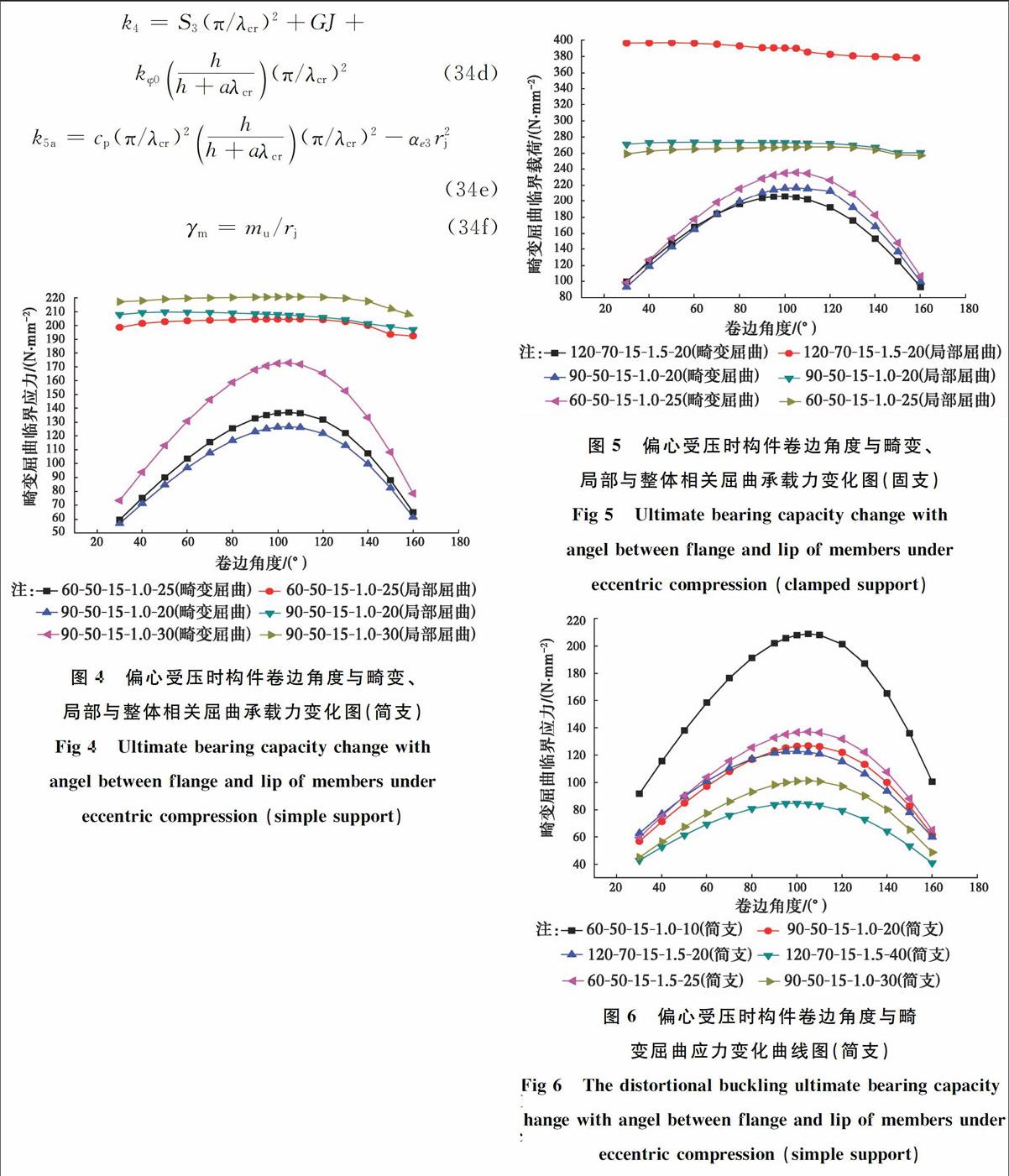
為了確定構件最后主導的屈曲模式，觀察卷邊角度變化分別對畸變屈曲、局部與整體相關屈曲的影響，本節選取部分試樣尺寸進行計算。按角度θ由30°到160°，每間隔5°～10°計算其畸變、局部與整體相關屈曲承載力，計算結果如圖4～5所示。

由圖4、5可觀察出卷邊角度變化對構件局部與整體相關屈曲臨界應力影響不大，且局部與整體相關屈曲臨界應力均大于畸變屈曲臨界應力，構件失穩模式以畸變屈曲為主。故本文只計算斜卷邊角度對槽鋼畸變屈曲臨界應力的影響，如圖6、7所示。從圖中可觀察出構件在簡支與固支情況下卷邊角度位于[30°～160°]區問，偏心距e取10、20、25、30、40mm時。構件受壓時的畸變屈曲臨界應力峰值主要集中在95°～105°。

3.2結果分析

由圖4～7可見，隨著卷邊角度變化，槽鋼局部與整體相關屈曲臨界應力變化不大，而畸變屈曲臨界應力出現了先增大后減小的變化過程。由此可見，卷邊角度的改變可以顯著改變構件的畸變屈曲臨界應力。

通過對最優角度的尋找，及最優角度對應的畸變屈曲臨界應力計算，觀察表1～2可知，無論是兩端簡支還是兩端固支，無論是不同偏心距還是不同尺寸試樣，其最優角度的畸變屈曲臨界應力與標準（卷邊角度為90°）構件的畸變屈曲臨界應力相比較均有提升，畸變屈曲承載力峰值主要集中在95°～105°。

觀察表1～2可知，無論簡支還是固支情況下，不同構件在不同偏心距受壓下畸變屈曲臨界應力隨卷邊角度變化的趨勢是一致的。其峰值主要集中在95°～105°，較標準角度（90°）均有不同程度的提高，最大可提升構件畸變屈曲臨界應力的3.5%，提高值為1203N·cm。

4.結論

1）通過CUFSM計算斜卷邊槽鋼在不同偏心距受壓情況下畸變屈曲臨界應力，計算結果顯示，隨著卷邊角度的變化，當卷邊角度大于90°時，構件畸變屈曲臨界應力都有著不同幅度的提升，而局部與整體相關屈曲臨界應力則沒有明顯的變化。

2）本文提出的將Yao-Teng推導的畸變屈曲臨界應力計算公式（偏心受壓）與遺傳算法相結合的技術，可以快速準確地找到最優的卷邊角度，可為工程人員設計提供參考。

3）據優化結果分析，構件處于兩端簡支或固支約束條件下，偏心距一定范圍內，使受壓構件的畸變屈曲臨界應力最大的最優卷邊角度范圍均集中在95°～105°。此外，為了方便工程師設計，建議卷邊角度可統一采用100°。