線性半向量二層規劃問題樂觀最優解的極點檢驗方法

劉敏，呂一兵，陳忠

(長江大學信息與數學學院，湖北 荊州 434023)

線性半向量二層規劃問題樂觀最優解的極點檢驗方法

劉敏，呂一兵，陳忠

(長江大學信息與數學學院，湖北 荊州 434023)

針對線性半向量二層規劃問題的特殊結構，首先采用標量化技術將上述線性半向量二層規劃問題轉化為一般的二層單目標規劃問題，然后采用以下層問題的Kuhn-Tucker最優性條件代替原問題的方法將其轉化為含互補約束的優化問題，并取互補約束為罰項，構造相應的罰問題，同時分析罰問題最優解的性質，最后基于罰問題最優解的性質設計了線性半向量二層規劃問題“樂觀最優解”的極點檢驗方法。

半向量二層規劃；罰函數；極點；樂觀最優解

考慮如下線性半向量二層規劃問題，

(1)

其中，x∈Rn,y∈Rm,b∈Rp,A1∈Rp×n,A2∈Rp×m,c∈Rn,c′∈Rm,D∈Rl×m。在上述半向量二層規劃問題中，其下層問題：

(2)

為包含上層決策變量x的線性多目標優化問題。因此，對于給定的上層決策變量x，下層問題以有效解集或者弱有效解集的形式反饋給上層。由于下層問題的有效解集或者弱有效解集中的元素一般不是唯一的，這就意味著半向量二層規劃問題本質上屬于下層有不唯一最優解的一類二層規劃問題。對于下層有不唯一最優解的二層規劃問題，其最優解定義一般采用“樂觀最優解”或者“悲觀最優解”[1,2]。筆者考慮上述問題(1)的“樂觀最優解”，即考慮如下線性半向量二層規劃問題：

(3)

半向量二層規劃最早由Bonnel 和Morgan在文獻[3]中提出，近年來逐步引起了國內外研究者的關注。在線性半向量二層規劃問題(3)的“樂觀最優解”的研究方面，呂一兵和萬仲平[4]以下層問題的互補約束為罰項，構造了罰問題并通過分析罰問題最優解的相關性質，設計了該類半向量二層規劃問題的“樂觀最優解”的全局優化算法；Ankhili和Mansouri[5]以下層問題的邊緣函數為罰項，構造了相應的罰問題，證明了罰函數的精確性并給出了罰函數算法；Zheng和Wan[6]將上層目標函數估計值與下層問題的邊緣函數同時作為罰項，提出了一種包含2個罰因子的罰函數方法，同時證明了罰函數的精確性；Calvete和Galve[7]將該類半向量二層規劃問題轉化為非凸約束域上的優化問題，并分別設計了Kth-算法及遺傳算法，同時給出了數值實驗結果；最近，Ren和Wang[8]將其轉化為含對偶間隙約束條件的單層優化問題，構造出對偶間隙指標函數并取其為罰項，得到了相應的罰問題，證明了罰函數的精確性并設計了罰函數算法；另外，Lv和Wan[9]首先將該類半向量二層規劃問題轉化為非光滑優化問題，然后采用松弛技術逼近原問題的可行域，最后設計了求解原問題近似最優解的算法。下面，筆者針對線性半向量二層規劃問題的特殊結構，采用標量化技術將上述線性半向量二層規劃問題(3)轉化為一般的二層單目標規劃問題，構造了相應的罰問題，通過分析罰問題最優解的相關性質設計了線性半向量二層規劃問題“樂觀最優解”的極點檢驗方法。

1 相關定義及理論結果

記S={(x,y)|Ax+By≤b,x≥0,y≥0}為問題(3)的約束域，同時對于給定的上層決策變量x，記S(x)為下層問題(2)的弱有效解集。

定義1 若點(x,y)∈IR={(x,y)|(x,y)∈S,y∈S(x)}，則稱(x,y)為問題(3)的可行解。

定義2 點(x*,y*)∈IR為問題(3)的局部最優解, 如果存在(x*,y*)的某個鄰域U，使得對任意的(x,y)∈IR∩U,有cx+c′y≤cx*+c′y*。

為了確保所討論的問題存在最優解，假設下列條件成立：

(A)問題(3)的可行域IR為非空緊集。

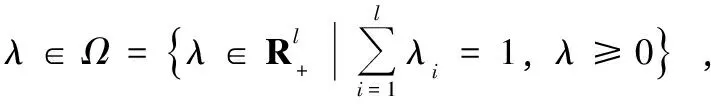
因此，問題(3)可以轉化為：

(4)

在上述問題(4)中，以下層問題的最優性條件代替下層問題，可以將問題(4)轉化為：

(5)

其中，u∈Rp,v∈Rm為Lagrange乘子。

問題(5)為帶互補約束的線性規劃問題，考慮將互補約束uT(b-A1x-A2y)=0,vTy=0作為罰項加入到上層目標函數，得到如下罰問題：

(6)

下面將分析問題(6)的最優解的相關性質，并以此為基礎設計相應的求解算法。

記：

Z={(x,y)|A1x+A2y≤b,x≥0,y≥0}

且Zv,Wv分別表示集合Z,W的頂點集。

定理1 假設給定(λ,u,v)∈W以及罰因子K，問題：

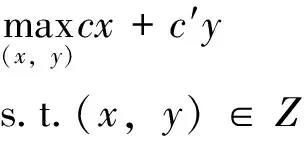
(7)

的某個最優解(x*,y*)可在集合Z的頂點處取得，即(x*,y*)∈Zv。

證明 對于給定的(λ,u,v)∈W以及罰因子K，問題(7)為線性規劃問題。顯然，問題(7)的某個最優解(x*,y*)∈Zv。證畢。

由定理1可以得到如下定理2。

定理2對于某個罰因子K，罰問題(6)的某個最優解(x*,y*,λ*,u*,v*)可在其可行域的頂點處取得，即(x*,y*,λ*,u*,v*)∈Zv×Wv。

證明 假設(x*,y*)∈Zv為問題(6)的某個最優解。對于問題(6)，由于其目標函數cx+c′y-K(uT(b-A1x-A2y)+vTy)為(λ,u,v)的線性函數，且W為多面體，則下列線性規劃問題：

其某個最優解(λ*,u*,v*)必可在可行域W的頂點處取得，即 (λ*,u*,v*)∈Wv。證畢。

上述2個定理表明，罰問題(6)的最優解可以在其可行域的某個頂點處取得。下面將證明在罰問題(6)的最優解處，其罰項為零。

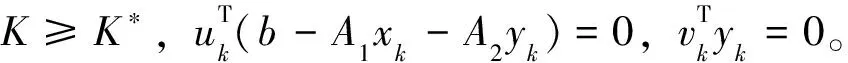
證明 假設(x*,y*,λ*)為問題(4)的最優解，則存在Lagrange乘子u*∈Rp,v*∈Rm，使得問題(4)的下層問題的最優性條件滿足，即:

-(λ*)TD+(u*)TA2-(v*)T=0 (u*)T(b-A1x*-A2y*)=0 (v*)Ty*=0

假設點(xk,yk,λk,uk,vk)為問題(6)的最優解，則有：

簡單運算后可得：

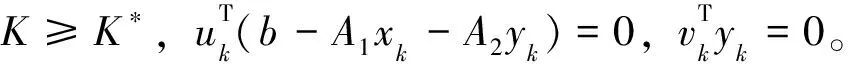
基于上述定理1、定理2和定理3，可以設計如下求解線性半向量二層規劃問題“樂觀最優解”的極點搜索算法。

2 算法

算法步驟如下：

步1 將線性半向量二層規劃問題轉化為問題(5)，同時采用相關方法求出Z和W的頂點集Zv,Wv。

步2 選擇點(x,y,λ,u,v)∈Zv×Wv，且滿足uT(b-A1x-A2y)=0以及vTt=0。

步3 將步1中得到的候選點分別帶入上層目標函數，同時比較目標函數的值得到相應的最優解。

3 算例

為了說明算法的實現過程，考慮如下半向量二層規劃問題[10]，文獻中其最優解為(x,y,z)=(3,0,0)。

求出集合Z和W的頂點集：

Zv={(3,0,1),(1,0,2),(3,0,0),(0,1,2),(0,3,0)}

在上述頂點集中，選擇使得互補條件uT(b-A1x-A2y)+vTy=0滿足的組合。

將上述滿足條件的頂點組合帶入目標函數并比較大小可知，頂點(x,y,z)=(3,0,0)為上述線性半向量二層規劃問題的最優解。

上述算例表明，筆者設計的極點檢驗方法對求解線性半向量二層規劃問題是可行的。

4 結語

利用線性半向量二層規劃問題的特殊結構，通過構造罰問題并分析其“樂觀最優解”的相關性質設計了求解其“樂觀最優解”的極點檢驗方法。簡單的算例表明，所設計的算法是可行的。值得指出的是，筆者提出的算法依賴于多面體頂點的有效獲取。然而，目前如何有效的獲得多面體的全部頂點依然是一個具有挑戰性的問題。倘若能夠有效的獲得多面體的全部頂點，那么所設計的算法將具有良好的計算前景。

[1]DempeS.Foundationsofbilevelprogramming[M].London:KluwerAcademicPublishers,2002.

[2]滕春賢,李智慧. 二層規劃的理論與應用 [M].北京: 科學出版社,2002.

[3]BonnelH,MorganJ.Semivectorialbileveloptimizationproblem:Penaltyapproach[J].JournalofOptimizationTheoryandApplications, 2006, 31(3): 365～382.

[4]呂一兵，萬仲平. 線性半向量二層規劃問題的全局優化方法[J]. 運籌學學報，2015, 19(2):29～36.

[5]AnkhiliZ,MansouriA.Anexactpenaltyonbilevelprogramswithlinearvectoroptimizationlowerlevel[J].EuropeanJournalofOperationalResearch, 2009, 197(1):36～41.

[6]ZhengY,WanZM.Asolutionmethodforsemivectorialbilevelprogrammingproblemviapenaltymethod[J].JournalofAppliedMathematicsandComputing, 2011(37):207～219.

[7]CalveteHI,GaleC.Onlinearbilevelproblemswithmultipleobjectivesatthelowerlevel[J].Omega, 2011, 39(1):33～40.

[8]RenAH,WangYP.Anovelpenaltyfunctionmethodforsemivectorialbilevelprogrammingproblem[J].AppliedMathematicsModelling, 2016(40):135～149.

[9]LvYB,WanZM.Asolutionmethodfortheoptimisticlinearsemivectorialbileveloptimizationproblem[J].JournalofInequalitiesandApplications,2014:164.

[10]CalveteHI,GaleC.Onlinearbilevelproblemswithmultipleobjectivesatthelowerlevel[J].Omega, 2011(39):33～40.

[編輯] 洪云飛

2016-11-16

國家自然科學基金項目(11201039)。

劉敏(1979-)，女，碩士生，現主要從事最優化理論與算法方面的研究工作。

呂一兵(1979-)，男，博士，教授，現主要從事最優化理論與算法方面的教學與研究工作,30950045@qq.com。

O224

A

1673-1409(2017)01-0001-04

[引著格式]劉敏，呂一兵，陳忠.線性半向量二層規劃問題樂觀最優解的極點檢驗方法[J].長江大學學報(自科版)，2017,14(1)：1～4.