一類常利率下帶干擾的雙險種風險模型

劉揚,何先平

(長江大學信息與數學學院，湖北 荊州 434023)

一類常利率下帶干擾的雙險種風險模型

劉揚,何先平

(長江大學信息與數學學院，湖北 荊州 434023)

討論了一類常利率下帶干擾、保單收取次數為復合Poisson過程、保險賠付次數服從負二項分布的風險模型，運用鞅方法和盈余過程的性質得到了破產概率的表達式和Lundberg不等式。

風險模型；破產概率；鞅；Poisson過程

瑞典精算師Filip Lundberg于1903年首次將Poisson過程引入破產理論研究，時至今日，破產理論日益豐富，已成為一門應用數學模型來描述和研究保險公司經營的重要學科。經典風險模型[1,2]用常數速率考慮保費的收取問題，但實際生活中無論是保費的到達還是險種的賠付往往是隨機的，所以有必要將經典的風險模型加以推廣。文獻[3]引入了廣義雙險種模型，但未考慮利率因素對模型的影響。文獻[4]加入了利率因素，但沒考慮市場通貨膨脹及保險公司本身的不確定因素形成的干擾。文獻[5]引入了隨機擾動項對模型的影響，文獻[6]進一步將模型推廣到常利率下帶干擾的風險模型，但單位時間內保費的收入為常數，文獻[7]豐富了保費收入，建立了保費收入和理賠均為復合Poisson過程的風險模型。筆者將單一險種推廣為雙險種，為考慮干擾項和常利率因素，假設保費收取次數為Poisson過程，理賠次數符合負二項分布，建立了常利率下帶干擾的雙險種風險模型，最終求解出新模型的破產概率表達式和Lundberg不等式。

1 模型的建立

設u≥0 ，以下隨機變量都定義在給定的概率空間(Ω，F,P) 上,建立風險模型：

式中，U(t)，S(t)分別表示保險公司在時刻t的盈余與盈利；u為保險公司的初始資本；c為常數，是保險公司單位時間內收取的保費；常數i表示利率；M(t)表示在[0,t]內收到的保單總數，且服從參數為λt的Poisson分布；Nj(t)(j=1,2)分別表示第j險種在[0,t]內發生的理賠次數，且分別服從參數為(t,pj)(00為干擾因子； {Xi,i≥1},{Yi,i≥1},{Zi,i≥1},{M(t),t≥0},{N1(t),t≥0},{N2(t),t≥0},{W(t),t≥0}是相互獨立的。

定義1T=inf{t|U(t)<0}為破產時刻，若對任意t≥0,均有U(t)≥0，即破產不會發生，記T=∞。則在初始資金為u的條件下，保險公司的最終破產概率為：

ψ(u)=P{T<∞|U(0)=u}

為保證公司穩定經營，要求單位時間內平均保費收入大于平均理賠額，即：

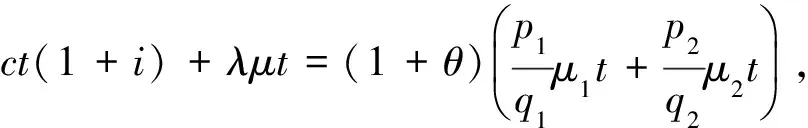
2 主要結果

引理1 盈利過程{S(t),t=0,1,2,…}具有平穩獨立增量。

定理1 對于盈利過程{S(t),t=0,1,2,…} ，存在函數g(r)，使得E[e-rS(t)]=etg(r)。

證明 因為：

=etg(r)

所以：

其中，MX(-r)、MY(r)、MZ(r)分別為Xi、Yi、Zi的矩母函數。

定理2 方程g(r)=0在(0,+∞)存在唯一的正解R，稱R為調節系數。

證明 由于：

因為g″(r)>0，所以曲線g(r)在r>0內是上凹的，g′(r)在r>0內單調遞增，且：

又因為r→+∞時，g′(r)→+∞，所以存在r1∈(0,+∞),使得g′(r1)=0，從而g(r1)為g(r)在(0,+∞)上的極小值。

又因為g(0)=0,r→∞時,g(r)→∞,所以g(r)=0在(0,+∞)存在唯一的正解R。

定理3 對于盈利過程{S(t),t≥0}，定義事件域：

令:

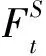
證明 對于任意t1∈[0,t]，由定理1有：

=Mu(t1)

定理4 在風險過程{U(t),t≥0}下，設R為調節系數，則最終破產概率為：

證明

E{exp}[-rU(t)]}=E{exp[-rU(t)]|T≤t}P(T≤t)

+E{exp[-rU(t)]|T>t}P(T>t)

(1)

因為：

所以式(1)左端可以寫為：

由定理2，取r=R，有g(R)=0,E[e-RU(t)]=e-Ru(1+i)，則式(1)變為：

e-Ru(1+i)=E[e-RU(t)|T≤t]P(T≤t)+E[e-RU(t)|T>t]P(T>t)

(2)

又因為：

U(t) =U(T)+(U(t)-U(T))

所以式(2)右端第1項：

E[e-RU(t)|T≤t]P(T≤t)

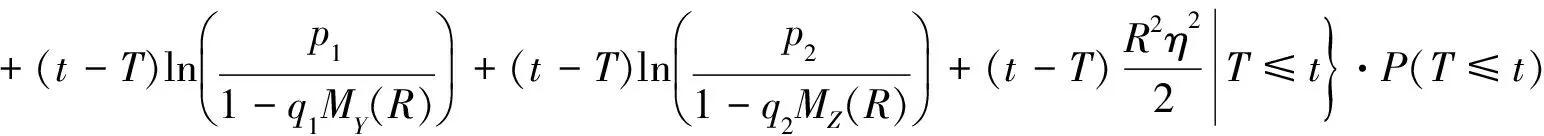
=E[e-RU(T)+(t-T)g(R)|T≤t]P(T≤t)=E[e-RU(T)|T≤t]P(T≤t)

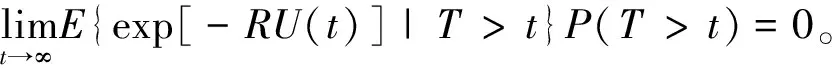
因為:

E{exp[-RU(t)]|T>t}P(T>t)=E[e-RU(t)·I(T>t)]≤E[e-RU(t)·I(U(t)>0)]

式中,I(T>t)為{T>t}的示性函數。

又因為0≤e-RU(t)·I(U(t)>0)≤1，故由強大數定律可得：

由Lebesgue控制收斂定理得：

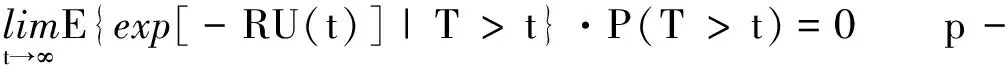
于是當t→∞時，式(2)可化簡為：

e-Ru(1+i)=E{exp[-RU(t)]|T≤t}ψ(u)

即：

推論1 在上述風險過程{U(t),t≥0}下，最終破產概率ψ(u)符合Lundberg不等式，即ψ(u)≤exp[-Ru(1+i)]，e-Ru(1+i)為ψ(u)的Lundberg上界。

3 結語

在經典風險模型的基礎上，加入了利率因素和通貨膨脹、管理者自身等不確定因素造成的擾動項，最終得到了新模型的破產概率一般表達式及破產概率上界，加深和豐富了風險模型的討論。但隨著保險業的發展，險種類別愈加多樣化，險種不僅局限在相互獨立的狀態下，還出現了相關聯的情況。今后該模型可在險種間的保費到達過程、索賠到達過程及干擾項的相關性問題上做出進一步改進，實現可以為風險預警和控制提供重要指標、更加貼近現實需要的風險模型。

[1]GrandellJ.AspectsofRiskTheory[M] .NewYork:SpringerVerlag， 1991.

[2] 蔣志明, 王漢興. 一類多險種風險過程的破產概率[J]. 應用數學與計算數學學報, 2001,14 (1):9～16.

[3] 郭立娟, 劉冬元. 一類廣義雙險種二項風險模型的破產概率[J]. 數學理論與應用, 2007, 27 (4):49～52.

[4] 陳奕含，楊璐. 一類帶干擾的離散風險模型[J]. 佳木斯大學學報, 2015,33(1):140～141.

[5] 陳鳳麗, 施齊焉. 一類雙險種風險模型的破產概率研究[J]. 福州大學數學報, 2012, 40 (4):449～452.

[6] 呂偉春, 陳新美. 常利率下帶干擾的雙險種風險模型[J]. 湖南文理學院學報, 2010, 22 (1):7～9.

[7] 贠小青. 帶干擾的泊松風險模型的破產概率及推廣[J]. 統計與決策, 2013,373(1):18～21.

[編輯] 洪云飛

2016-09-27

國家自然科學基金項目(60873021/F0201)。

劉揚(1986-)，女，碩士生，現主要從事數理統計、風險模型方面的研究工作。

何先平(1964-)，男，碩士，教授，現主要從事數理統計方面的教學與研究工作,hxp@yangtzeu.edu.cn。

O211.6

A

1673-1409(2017)01-0036-04

[引著格式]劉揚,何先平.一類常利率下帶干擾的雙險種風險模型[J].長江大學學報(自科版)，2017,14(1)：36～39.