Henstock積分Newton-Leibniz公式的簡(jiǎn)捷證明
李偉
(集美大學(xué)理學(xué)院, 福建 廈門 361021)
宋述剛
(長江大學(xué)信息與數(shù)學(xué)學(xué)院,湖北 荊州 434023)
Henstock積分Newton-Leibniz公式的簡(jiǎn)捷證明
李偉
(集美大學(xué)理學(xué)院, 福建 廈門 361021)
宋述剛
(長江大學(xué)信息與數(shù)學(xué)學(xué)院,湖北 荊州 434023)
Newton-Leibniz公式是微積分學(xué)基本定理的一個(gè)重要應(yīng)用,其建立了定積分與被積函數(shù)的原函數(shù)之間的聯(lián)系,使得計(jì)算定積分問題從求和式的極限轉(zhuǎn)化為求被積函數(shù)的原函數(shù)值差的問題。在Riemann積分、Lebesgue積分、Newton積分和δ(x)精細(xì)分劃的基礎(chǔ)上,建立了Henstock積分有關(guān)的基本概念,簡(jiǎn)述了Henstock引理及其證明,由此給出Henstock積分中的Newton-Leibniz公式,并給予簡(jiǎn)捷證明。
Riemann積分;δ(x)精細(xì)分劃;Henstock積分;連續(xù)函數(shù)
Riemann積分[1](簡(jiǎn)稱R-積分)建立之后,1902年在測(cè)度論[2]的基礎(chǔ)上又建立了Lebesgue積分[3](簡(jiǎn)稱L-積分)。L-積分推廣了R-積分,但不是R-積分的全部推廣,比如廣義R-可積不一定是L-可積。從空間完備化觀點(diǎn)看,L-積分不過是C[a,b](連續(xù)函數(shù)類)中函數(shù)R-積分的一種完備化擴(kuò)張[4],可見L-積分具有一定的局限性。因此,人們一直試圖尋找一種新的積分。1957~1958年,R.Henstock建立了一種完全Riemann型的積分,稱為Henstock積分[5](簡(jiǎn)稱H-積分)。H-積分的本質(zhì)是“非絕對(duì)型”的,因此有時(shí)也稱之為非絕對(duì)型積分。H-積分既推廣了L-積分,又包括了Newton積分[6](簡(jiǎn)稱N-積分)和反常R-積分。下面,筆者就非絕對(duì)型H-積分理論進(jìn)行研究:首先給出δ(x)精細(xì)分劃的定義,然后引進(jìn)區(qū)間[a,b]上的非絕對(duì)型H-積分,從而在Henstock引理的基礎(chǔ)上給出了H-積分中的Newton-Leibniz公式,并給予了簡(jiǎn)捷證明。
1 相關(guān)定義與引理
定義1[7]設(shè)δ(x)為區(qū)間[a,b]上的正值函數(shù),所謂[a,b]上的分劃D是δ(x)精細(xì)的,是指存在有序分點(diǎn)a=x0 ξi-δ(ξi) 即: ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 定義2[5]稱實(shí)函數(shù)f(x)在區(qū)間[a,b]上Henstock可積,其積分值為A,如果對(duì)?ε>0,?實(shí)函數(shù)δ(x)>0,對(duì)區(qū)間[a,b]上任作δ(x)精細(xì)分劃D: a=x0 ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 當(dāng)ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi))(i=1,2,…,n)時(shí),總有: 或簡(jiǎn)記為: 其中,[u,v]為分劃D中典型區(qū)間,滿足: ξ-δ(ξ) 若f(x)在[a,b]上Henstock可積(以下簡(jiǎn)稱為H-可積),其積分記為: 定義2與R-積分不同之處在于: 1)R-積分定義中要求δ是正常數(shù),這里的δ(x)為一正值函數(shù)而非常數(shù); 2)R-積分定義中先取x1,x2,…,xn-1,再取ξ1,ξ2,…,ξn,此處先取ξ1,ξ2,…,ξn,對(duì)每一點(diǎn)ξi,有ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi)),(i=1,2,…,n),假如以上區(qū)間組成一[a,b]的覆蓋,那么便能取x1,x2,…,xn-1符合以上條件。注意,集合{(ξ-δ(ξ),ξ+δ(ξ));ξ∈[a,b]}形成一開覆蓋,根據(jù)Heine-Borel有限覆蓋定理,肯定能找到一分劃D={[u,v];ξ}符合條件ξ-δ(ξ) 例1 令: 則f(x)在[0,1]上是H-可積的。 證明 ?ε>0,記[0,1]中的有理數(shù)為r1,r2,…。令: 取δ(x)精細(xì)分劃D={[u,v];ξ},有(此處A=0): 式中, ∑1表示各項(xiàng)f(ξ)(v-u)中ξ為有理數(shù)時(shí)之和。故f(x)為H-可積,且: 注:定義在[0,1]上的Dirichlet函數(shù)是R-不可積的[8],但其是H-可積的,可見H-積分也是R-積分的推廣。 引理1 (Henstock引理[9]) 若f(x)在[a,b]上H-可積,且有原函數(shù)F(x): 則?ε>0,?δ(x)>0,使得對(duì)[a,b]上的任何δ(x)精細(xì)子分劃: a≤a1 ξi∈[ai,bi]?(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 有: 說明 精細(xì)子分劃是不要求[a,b]=∪[ai,bi]的精細(xì)分劃。 證明 由于f(x)在[a,b]上H-可積,故對(duì)?ε>0,在[a,b]上有δ(x)>0,凡δ(x)精細(xì)分劃所對(duì)應(yīng)的積分和,有: 這樣,每個(gè)Ji上的δi(x)精細(xì)分劃與ai,bi,ξi(i=1,2,…,n)構(gòu)成[a,b]上的δ(x)精細(xì)分劃,從而: ≤2ε 定理1 若f(x)為[a,b]上N-可積,則f(x)于[a,b]上H-可積。 證明 因f(x)∈N,故?連續(xù)函數(shù)F(ξ),有F′(ξ)=f(ξ),其中ξ∈[a,b],從而?ε>0,?δ(ξ)>0,當(dāng)ξ-δ(ξ) |F(v)-F(u)-f(ξ)(v-u)|<ε(v-u) 任作[a,b]的δ(x)精細(xì)分劃D: a=x0 ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 則有: =ε(b-a) 由ε的任意性得f(x)為H-可積。 定理2 設(shè)函數(shù)F(x)在[a,b]上連續(xù),且在[a,b]中除去一零測(cè)集(測(cè)度為0的集)E外,F(xiàn)′(x)=f(x),則f(x)在[a,b]上為H-可積,且: 證明 由假設(shè)令E={a1,a2,…}?[a,b],?x∈[a,b]-E,有F′(x)=f(x),故?ε>0,?δ(ξ)>0,ξ∈[a,b]-E,?u,v滿足ξ∈[u,v]?(ξ-δ(ξ),ξ+δ(ξ))時(shí),恒有: |F(v)-F(u)-f(ξ)(v-u)|<ε(v-u) 又因F(x)在[a,b]上連續(xù),故當(dāng)ξ=ai時(shí),?δi>0,使得當(dāng)u,v滿足ai∈[u,v]?[ai-δi,ai+δi]時(shí),有: |F(v)-F(u)|<ε·2-i a=x0 ξi∈[xi-1,xi]?(ξi-δ(ξi),ξi+δ(ξi))i=1,2,…,n 有: 其中,[u,v]為區(qū)間[a,b]上分劃D的典型區(qū)間;∑分成2項(xiàng)部分和∑1與∑2,∑1取當(dāng)ξ∈[a,b]-E時(shí)的部分和,∑2=∑-∑1。上述不等式的第2項(xiàng)中,當(dāng)ξ=ai時(shí),因: 故: f(ai)(v-u)<ε·2-i 例2 設(shè): 則: f(x)滿足定理2的條件,但f(x)不是L-可積的,而是H-可積的。 非絕對(duì)型H-積分推廣了L-積分,又包括了N-積分和反常R-積分。Newton-Leibniz公式在非絕對(duì)型H-積分理論中占有重要地位,但其證明在相關(guān)文獻(xiàn)中顯得較為復(fù)雜,筆者在Henstock引理的基礎(chǔ)上給出了該定理的一個(gè)簡(jiǎn)捷證明,改進(jìn)了相關(guān)文獻(xiàn)中的證明方法。 [1]李成章.數(shù)學(xué)分析(上冊(cè))[M].第2版.北京:科學(xué)出版社,2016:196~201. [2]DonaldLC.MeasureTheory[M].TheWorldBookPublishingCompany,2012:75~78. [3] 王晶昕,王煒,任詠紅.實(shí)變函數(shù)論[M].北京:科學(xué)出版社,2016:68~86. [4] 李忠寧.關(guān)于R可積函數(shù)空間的完備化[J].河西學(xué)院學(xué)報(bào),2010,26(5):14~18. [5]HenstockR.Lecturesonthetheoryintegration[M].WorldScientific,1988:13~19. [6] 同濟(jì)大學(xué)數(shù)學(xué)系.高等數(shù)學(xué)(上冊(cè))[M].第7版.北京:高等教育出版社,2014:238~243. [7] 丁傳松,李秉彝.廣義黎曼積分[M]. 北京:科學(xué)出版社,1989:5~8. [8] 何越.狄利克雷函數(shù)與黎曼函數(shù)的性質(zhì)[J].河南教育學(xué)院學(xué)報(bào)(自然科學(xué)版),2013,22(4):25~27. [9]YeeLP.LanzhouLecturesonHenstockIntegration[M].WorldScientific,1989:15~65. [編輯] 洪云飛 2016-11-15 福建省自然科學(xué)基金項(xiàng)目(2015J01585)。 李偉(1962-),男,副教授,現(xiàn)主要從事函數(shù)論方面的教學(xué)與研究工作。 宋述剛(1961-),男,教授,現(xiàn)主要從事函數(shù)論方面的教學(xué)與研究工作,2712281782@qq.com。 O171.2 A 1673-1409(2017)01-0040-04 [引著格式]李偉,宋述剛.Henstock積分Newton-Leibniz公式的簡(jiǎn)捷證明[J].長江大學(xué)學(xué)報(bào)(自科版),2017,14(1):40~43.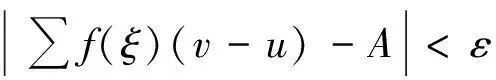
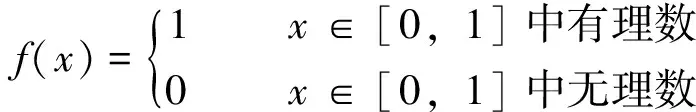

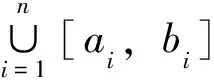
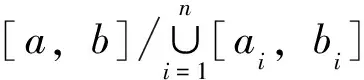
2 主要結(jié)論
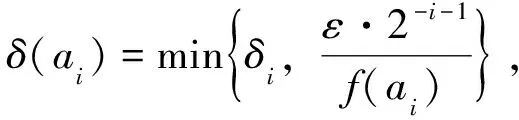
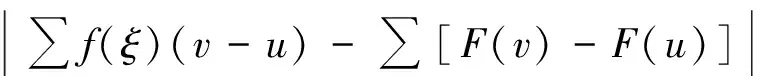
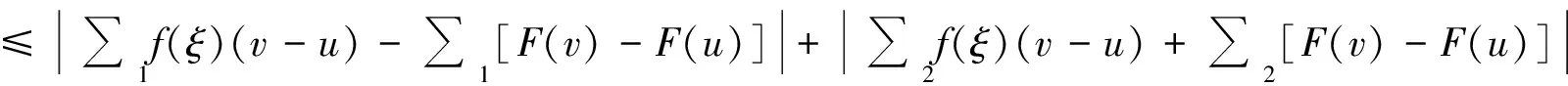
3 結(jié)語

