雙正態正態區間估計和假設檢驗的拓廣
劉國祥
(赤峰學院 數學與統計學院,內蒙古 赤峰 024000)
雙正態正態區間估計和假設檢驗的拓廣
劉國祥
(赤峰學院 數學與統計學院,內蒙古 赤峰 024000)
本文給出雙正態獨立總體下區間估計和假設檢驗的拓廣,主要推廣了總體均值的線性函數的區間估計和方差比不是1的假設檢驗方法.
正態分布;獨立性;區間估計;假設檢驗;數學期望;方差
一般的概率論與數理統計教材[2][3][4],都給出兩個正態總體下,均值差和方差比的區間估計和假設檢驗.現在將它們拓廣為一個數學期望是另一個的線性函數和兩個方差比不是1的情況的,給出置信區間估計和顯著性假設檢驗的方法.
多數教材上給出的兩個正態總體下統計量的基本性質是:
引理1(兩正態總體下統計量的基本性質)假定X,Y是相互獨立的兩個總體,且
總體X~N(μ1,σ12),樣本為(X1,X2,…,Xn1),
總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn1).
那么:


其中(1)是在已知方差,估計和檢驗均值差時用的.(2)是在未知方差,估計和檢驗均值差時用的,但是已知σ1=σ2=σ.(3)[2]是在未知方差,估計和檢驗均值差時用的,但是已知σ12≠σ22.(4)是在已知均值,估計和檢驗方差比時用的.(5)是在未知均值,估計和檢驗方差比時用的.
定理1假定X,Y是相互獨立的兩個總體,且
總體X~N(μ1,σ12),樣本為(X1,X2,…,Xn1),
總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn1),a,b∈R.
那么:在σ12,σ22已知時:

證明由于假定X,Y是相互獨立的兩個總體,且總體X~N(μ1,σ12),樣本為(X1,X2,…,Xn1).總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn2).a,b∈R.
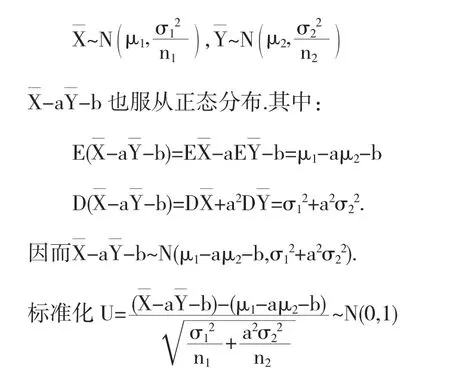
相應地,容易得到μ1-aμ2-b在1-α置信水平下的置信區間為

根據區間估計和假設檢驗之間的關系,可以得到原假設:
H0:μ1=aμ2+b的顯著性假設檢驗.
定理2假定X,Y是相互獨立的兩個總體,且
總體X~N(μ1,σ12),樣本為(X1,X2,…,Xn1),
總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn2).a,b∈R.
那么:在σ12,σ22未知時,在σ12=σ22=σ2下,有

μ1-aμ2-b在1-α置信水平下的置信區間為

證明由于假定X,Y是相互獨立的兩個總體,且總體X~N(μ1,σ12),樣本為(X1,X2,…,Xn1),總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn2).a,b∈R.
設Z=aY+b,那么,X,Z也獨立.
由于方差未知,那么:
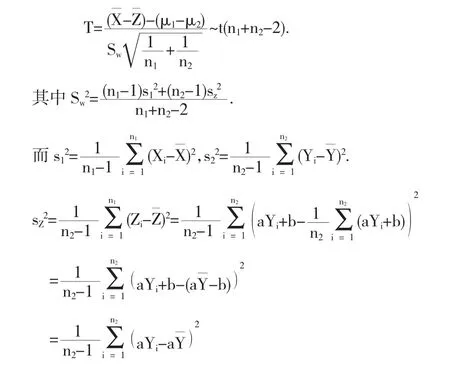

根據引理1之(4)、(5),容易得到:
引理2假定X,Y是相互獨立的兩個總體,且總體X~N (μ1,σ12),樣本為(X1,X2,…,Xn1),總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn2).那么:
在μ1,μ2已知時,方差比在1-α置信水平下的置信區間為:

在μ1,μ2未知時,方差比在1-α置信水平下的置信區間為:

關于假設檢驗,一般文獻都給出σ12=σ22,或者說的檢驗.那么我們如果要檢驗=a,未見文獻論述.下面拓廣假設檢驗的應用.
定理3假定X,Y是相互獨立的兩個總體,且總體X~N (μ1,σ12),樣本為(X1,X2,…,Xn1),總體Y~N(μ2,σ22),樣本為(Y1,Y2,…,Yn2).a,b∈R+.那么:
關于原假設H0:σ12=aσ22,或者
在μ1,μ2已知時,如果1屬于置信區間(10),則,接受原假設,否則就拒絕.
在μ1,μ2未知時,如果a屬于置信區間(11),則,接受原假設,否則就拒絕.
根據區間估計和假設檢驗之間的關系,可以證明[3],這里略去.
關于兩個正態總體的單側區間估計和單側假設檢驗的相應結論,容易列出.
例 1[5]甲種產品長度X~N(μ1,5),乙種產品長度Y~N (μ2,1),甲乙獨立.現在在甲種產品中抽取4只,測得長度分別是:4.0,4.2,4.6,5.0.在乙種產品中抽取5只,測得長度分別是:2.0,2.3,2.1,2.5,2.8.能否認為甲種產品長度是乙種產品長度的2倍?顯著水平α=0.05.
這是兩個正態總體均值的假設檢驗問題,已知方差σ12=5,σ22=1.
根據定理1,提出原假設和備選假設H0:μ1-2μ2=0,H1:μ1-2μ1≠0.


所以接受原假設,也就是可以認為甲種產品長度是乙種產品長度的2倍.
相應地,容易得到μ1-2μ2在1-α=1-0.05=0.95置信水平下的置信區間為
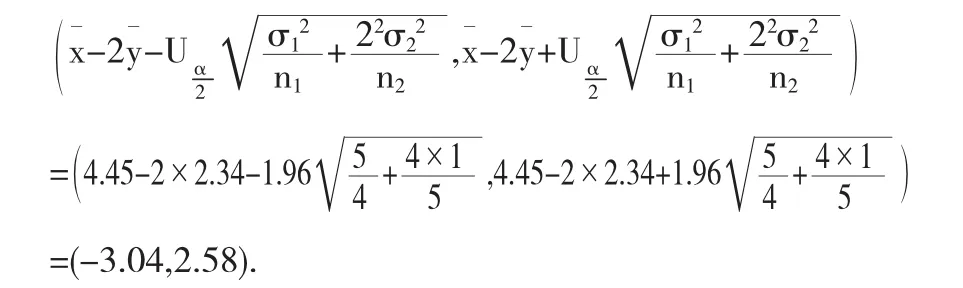
1∈(-3.04,2.58),所以可以認為μ1-2μ2=0,或者說μ1=2μ2.
注意,這里置信區間比較大的原因是題目中數學期望比較小,而方差比較大的緣故.
例2[4]某自動機床加工同類型套筒,假設套筒的直徑服從正態分布,現在從兩個班次的產品中個抽檢5個套筒,測量它們的直徑,得如下數據:
A班:2.066,2.063,2.068,2.060,2.067.
B班:2.058,2.057,2.063,2.058,2.060.
這就是(11)的情況,計算得:


這個問題改為,其它條件不變,問在α=0.10時,
能否接受σ12=0.5σ22?,0.5∈(0.316,12.901),當然接受.
能否接受σ12=σ12?,1∈(0.316,12.901),當然接受.
能否接受σ12=5σ22?,5∈(0.316,12.901),當然接受.
能否接受σ12=10σ22?,10∈(0.316,12.901),當然接受.
能否接受σ12=20σ22?,20∈(0.316,12.901),當然不能接受.
一般情況下,方差和方差比的變動都比較大,出現這樣結果不奇怪.
〔1〕劉國祥,張曉麗,楊永霞,等.應用型人才培養模式下概率論與數理統計課程改革探索與實踐[J].赤峰學院學報(自然科學版),2014(12).
〔2〕賈俊平,何曉群.統計學(第六版)[M].北京:中國人民大學出版社,2015.160-189.
〔3〕浙江大學,盛驟,謝式千,潘承毅.概率論與數理統計(第四版)[M].北京:高等教育出版社,2008.192-193.
〔4〕武漢大學數學與統計學院,齊民友,劉祿勤,龔小慶,王文祥.概率論與數理統計[M].北京:高等教育出版社,2002.190-193.
〔5〕碩士研究生入學統一考試數學命題研究中心,數學復習輔導——概率論與數理統計[M].上海:上海交通大學出版社,2010.128.
〔6〕劉國祥,楊永霞,張曉麗,等.基于應用型人才培養模式下的貝葉斯公式教學[J].赤峰學院學報(自然科學版),2015(01).
O212.1
A
1673-260X(2017)02-0010-03
2016-12-10

