自適應(yīng)空間機動目標(biāo)跟蹤算法

林浩申，劉剛，何兵

火箭軍工程大學(xué)，西安 710025

自適應(yīng)空間機動目標(biāo)跟蹤算法

林浩申，劉剛*，何兵

火箭軍工程大學(xué)，西安 710025

在空間目標(biāo)跟蹤問題中，目標(biāo)機動導(dǎo)致的模型不匹配問題會導(dǎo)致濾波算法出現(xiàn)滯后現(xiàn)象。為了對空間機動目標(biāo)進行快速跟蹤，在平方根容積卡爾曼濾波(Square-root Cubature Kalman Filter，SCKF)的基礎(chǔ)上，引入強跟蹤濾波(StrongTracking Filter，STF)的思想，推導(dǎo)得到了次優(yōu)漸消因子在SCKF中的等價描述。并通過建立以矩匹配方法為基礎(chǔ)的自適應(yīng)機制，設(shè)計了兼顧濾波精確性和魯棒性的自適應(yīng)強跟蹤平方根容積卡爾曼濾波(Adaptive Strong Tracking Square-root Cubature Kalman Filter，AST-SCKF)算法。仿真結(jié)果表明，在目標(biāo)機動前，AST-SCKF算法和SCKF算法的位置收斂精度相差不足1%；在目標(biāo)機動后，AST-SCKF算法的位置和速度的收斂精度相對SCKF算法分別提高了95.19%和30.50%，同時，其收斂速度相對SCKF算法分別提高了57.20%和24.68%。

空間目標(biāo)定位；機動目標(biāo)；僅測角；自適應(yīng)濾波；容積卡爾曼濾波；強跟蹤濾波；漸消因子；機動檢測

隨著空間技術(shù)的不斷發(fā)展，空間目標(biāo)的實時機動技術(shù)成為完成復(fù)雜空間任務(wù)的關(guān)鍵技術(shù)之一，因此，如何對機動目標(biāo)進行快速跟蹤和精確定軌成為了空間目標(biāo)監(jiān)視領(lǐng)域的核心問題。

天基觀測平臺憑借其不受天氣、國界等因素影響的特點得到廣泛的應(yīng)用，其中依靠目標(biāo)輻射的光學(xué)信號或無線信號等方式進行無源探測的方式，因其隱蔽性好、耗能少等優(yōu)點1]成為空間監(jiān)視的重要手段，因此本文重點研究天基平臺無源定位問題。

在空間目標(biāo)無源定位問題具有維度高和非線性強的特點，當(dāng)目標(biāo)不機動時，常用的擴展卡爾曼濾波(Extended Kalman Filter，EKF)、無跡卡爾曼濾波(Unscented Kalman Filter，UKF)UKF和容積卡爾曼濾波(Cubature Kalman Filter，CKF)等算法都能表現(xiàn)出滿意的跟蹤性能2]，但在目標(biāo)機動時，容易出現(xiàn)濾波算法收斂延遲以及精度不高的問題。為了解決目標(biāo)機動帶來的問題，文獻3-4]將次優(yōu)的漸消因子引入到EKF算法中，提出了強跟蹤濾波(Strong Tracking Filter，STF)算法，該算法通過在線調(diào)整濾波增益矩陣，保證輸出殘差保持相互正交，達(dá)到提取殘差中有效信息的目的，增強了算法對狀態(tài)突變和參數(shù)突變的抗擾動能力，但以EKF為基礎(chǔ)的STF算法不可避免地要計算復(fù)雜的雅克比矩陣。

文獻5]中提出了一種基于UKF的強跟蹤濾波器，文獻6]以此為基礎(chǔ)來產(chǎn)生粒子濾波中的密度函數(shù)，打破了傳統(tǒng)強跟蹤濾波算法中EKF所帶來的局限性，但UKF的參數(shù)設(shè)置的難度會隨著狀態(tài)維度的增加而增加7]，粒子濾波的計算量會隨著狀態(tài)維度的增加呈指數(shù)增長。近年來，基于求積容積方法的CKF算法被提出，其良好的性能使得其在姿態(tài)控制和導(dǎo)航等領(lǐng)域得到廣泛應(yīng)用8]。但計算機的舍入誤差會導(dǎo)致該算法的協(xié)方差矩陣出現(xiàn)非對稱和非正定性問題9]，為了解決這一問題，文獻10]提出了基于QR矩陣分解的平方根容積卡爾曼濾波(Square-root Cubature Kalman Filter，SCKF)算法。

因此本文重點研究了如何提高SCKF算法跟蹤機動目標(biāo)的能力，通過引入次優(yōu)漸消因子增強了算法的魯棒性，通過建立機動檢測機制兼顧了算法的精確性。仿真結(jié)果表明該算法能對空間機動目標(biāo)進行快速精確的跟蹤，具有一定的研究和實用價值。

1 基于天基測角的空間目標(biāo)被動跟蹤模型

1.1 空間目標(biāo)運動模型

由于地球中心的引力遠(yuǎn)大于其他作用力，通常可以采用由開普勒第一定律推導(dǎo)出的二體運動方程來描述航天器的運動11-12]。根據(jù)二體運動規(guī)律，在J2000.0坐標(biāo)系中，目標(biāo)的運動方程為

(1)

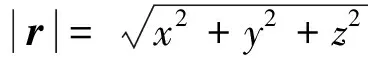
1.2 考慮地球非球形J2項攝動的運動模型

實際的空間目標(biāo)運動是一個非常復(fù)雜的過程，空間目標(biāo)會受到地球非球形攝動、地球大氣阻力攝動、太陽光壓攝動以及其他天體引力攝動12]，文獻13]比較了不同軌道高度上空間目標(biāo)所受到各種攝動的量級水平，結(jié)果表明：J2項非球形攝動為主要攝動力，尤其是針對低軌目標(biāo)。

考慮到J2項攝動，空間目標(biāo)的狀態(tài)微分方程為12]

(2)

式中：J2=1.082 626 1×10-3為地球引力場二階球諧系數(shù)，Re=6 378 136.0 m為地球平均赤道半徑。

1.3 考慮目標(biāo)機動的運動模型

隨著空間任務(wù)的日趨復(fù)雜，空間目標(biāo)在線機動越來越常見，軌道機動是指航天器在控制系統(tǒng)作用下，依靠其動力裝置，改變飛行軌道的過程14]。機動方式可按照推力的持續(xù)時間分為脈沖式機動和連續(xù)式機動。其中脈沖式機動需要優(yōu)化的參數(shù)少，并有成熟便捷的Lambert轉(zhuǎn)移理論支撐，得到廣泛應(yīng)用，因此本文僅考慮脈沖式機動，空間目標(biāo)在機動時刻獲得瞬時脈沖速度Δv=Δvx,Δvy,Δvz]，而位置保持不變。其中，Δvx,Δvy,Δvz分別表示目標(biāo)在軌道坐標(biāo)系中徑向、橫向和法向的速度增量。

1.4 僅測角觀測模型

假設(shè)天基平臺通過無源探測的方式僅獲得空間目標(biāo)的角度信息，對俯仰角βk和方位角δk定義如下15]：

(3)

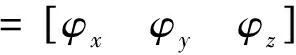
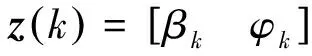
(4)

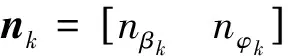
2 自適應(yīng)強跟蹤平方根容積卡爾 曼濾波(AST-SCKF)算法

2.1 次優(yōu)漸消因子的等價描述

文獻3]得出結(jié)論：但當(dāng)模型狀態(tài)突變時，為了保持輸出殘差序列的高斯白噪聲特性，通過在線調(diào)整濾波增益矩陣Kk，可以迫使濾波器保持對實際系統(tǒng)狀態(tài)量的跟蹤，為了提高系統(tǒng)的實時性，通常采用次優(yōu)算法計算漸消因子λk，次優(yōu)漸消因子的推導(dǎo)成為了強跟蹤算法的核心。文獻3]中在EKF的基礎(chǔ)上詳細(xì)推導(dǎo)了漸消因子λk的計算方法：

(5)

(6)

(7)

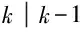
本文在SCKF中引入次優(yōu)的漸消因子后，需要對漸消因子重新推導(dǎo)計算，可以得到Nk和Mk的等價形式為

Nk=Vk-βRk-

(8)

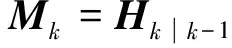
(9)

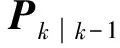
(10)

(11)

(12)

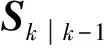
Nk=Vk-βRk-

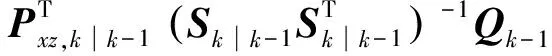
(13)

(14)

求得Nk和Mk后即可根據(jù)式(5)和式(6)計算漸消因子λk。

2.2 機動檢測

次優(yōu)漸消因子的引入，解決了空間目標(biāo)機動帶來的狀態(tài)突變問題，但在空間目標(biāo)未機動的情形下，漸消因子降低了原有SCKF算法的跟蹤精度。基于空間目標(biāo)機動能力和機動次數(shù)都受到燃料限制的特點，本文設(shè)計了一種基于機動檢測的自適應(yīng)濾波機制，其檢測方式如下：

(15)

式中：S≥1表示可調(diào)閾值系數(shù)，針對不同的實際背景，需要人為設(shè)置；γk表示殘差序列。若公式(15)成立，則表示目標(biāo)未進行機動；否則，則表示目標(biāo)進行了機動。

根據(jù)機動檢測的結(jié)果，當(dāng)未檢測到目標(biāo)機動時，濾波器保持在傳統(tǒng)的SCKF濾波狀態(tài)；當(dāng)檢測到目標(biāo)機動行為時，濾波器切換至帶漸消因子的SCKF算法狀態(tài)。

2.3 算法流程設(shè)計

文獻16]詳細(xì)給出了SCKF算法的推導(dǎo)過程及濾波流程；文獻3]詳細(xì)給出了STF算法的推導(dǎo)過程及濾波流程；根據(jù)前述部分的推導(dǎo)，本節(jié)所提出的AST-SCKF算法的計算步驟為：

1)濾波器初始化：

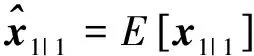
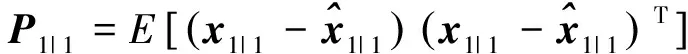
(16)

若k>1，則執(zhí)行步驟2)～步驟5)。

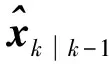
3)根據(jù)式(15)進行目標(biāo)機動檢測，如果檢測到目標(biāo)機動則進入步驟4)，否則進入步驟5)。

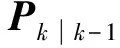
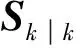
3 仿真結(jié)果及分析

3.1 作戰(zhàn)想定

假設(shè)高軌道的天基觀測平臺通過無源探測的方式獲取低軌空間目標(biāo)的角度信息，并對空間目標(biāo)進行跟蹤，而空間目標(biāo)試圖通過一次脈沖式的強機動擺脫跟蹤。其中觀測平臺與空間目標(biāo)的軌道六要素(半長軸、偏心率、軌道傾角、升交點赤經(jīng)、近地點幅角、過近地點時刻)分別為：(10 508.1，0.000 577 8，63.244 7，231.733 5，144.160 8，0)和(6 708.9，0.000 490 3，42.782 6，66.624 8，315.370 6，0)以此為基礎(chǔ)，通過龍哥庫塔轉(zhuǎn)阿達(dá)姆斯積分方法得到理論軌道數(shù)據(jù)。

3.2 參數(shù)設(shè)置

假設(shè)目標(biāo)機動時刻為1 500s，在相對坐標(biāo)系內(nèi)的速度增量為Δv=30,30,30]m/s。

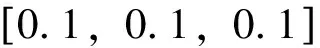
3.3 性能指標(biāo)

為了準(zhǔn)確描述算法的性能，便于算法性能的比較分析，設(shè)立如下標(biāo)準(zhǔn)：

1)均方根誤差：對k時刻的均方根誤差定義為

RMES (k)=

(17)

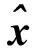
2)收斂時間：當(dāng)位置的RMES連續(xù)100s低于5 km時認(rèn)為位置收斂，當(dāng)速度的RMES連續(xù)100s低于5 m/s時認(rèn)為速度收斂。機動前的收斂時間以仿真零時刻為計時起點，機動后的收斂時間以機動時刻為計時起點。

3)收斂精度：以機動前一時刻的RMES作為機動前的收斂精度，以仿真結(jié)束時刻的RMES作為機動后的收斂精度。

3.4 仿真結(jié)果

分別采用SCKF算法和AST-SCKF算法對上述場景中的空間目標(biāo)進行跟蹤。仿真結(jié)果如圖1～圖3所示。

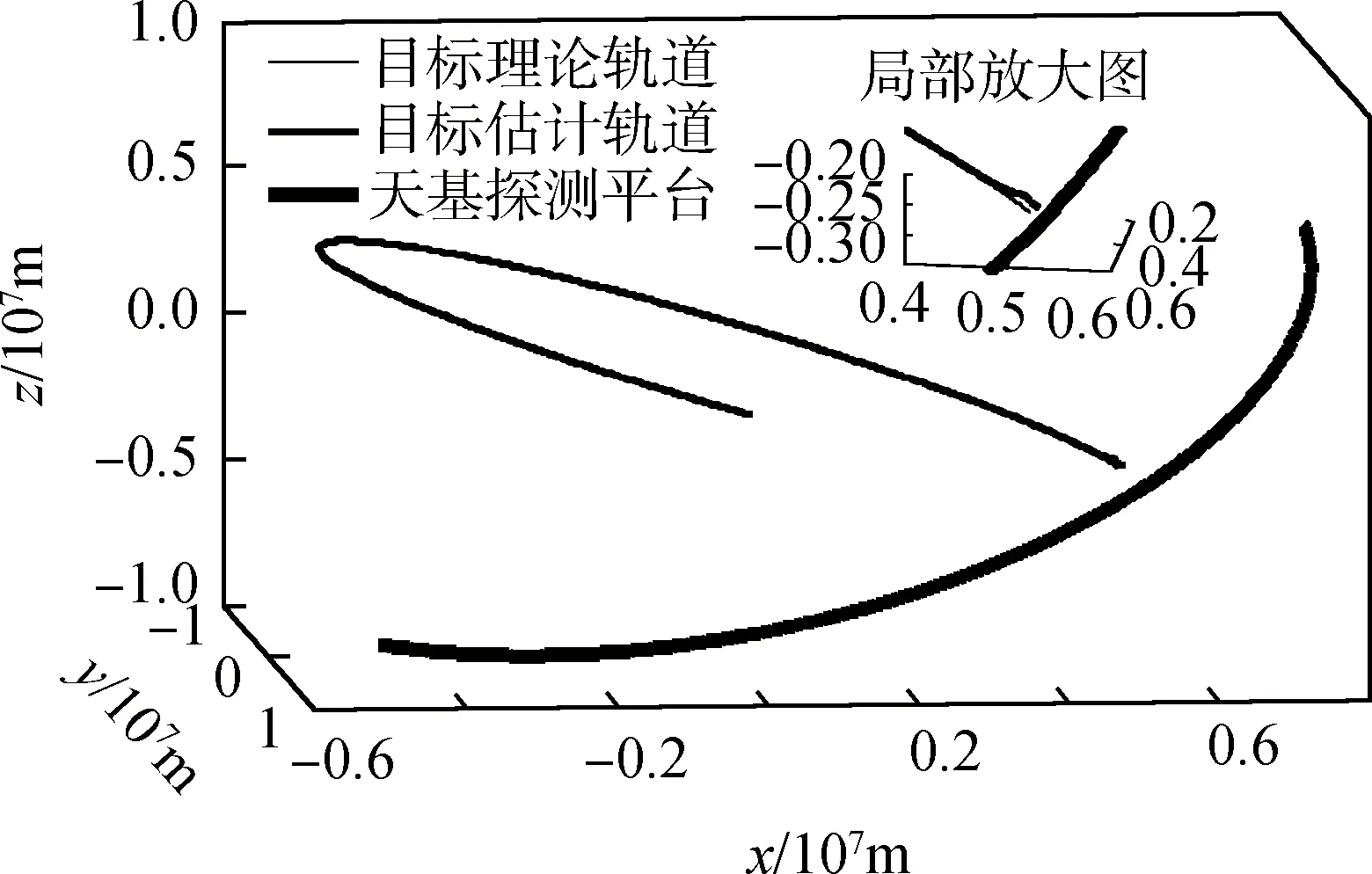
圖1 基于AST-SCKF算法的跟蹤效果Fig.1 Tracking effect based on AST-SCKF

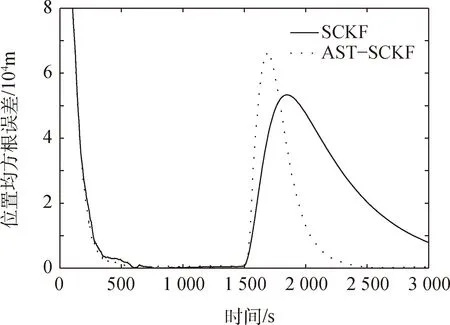
圖2 位置均方根誤差比較Fig.2 Comparison of position root-mean square error

分析圖2和圖3中的AST-SCKF算法的RMES曲線，可以得到該自適應(yīng)濾波器的狀態(tài)切換情況，如表1所示。

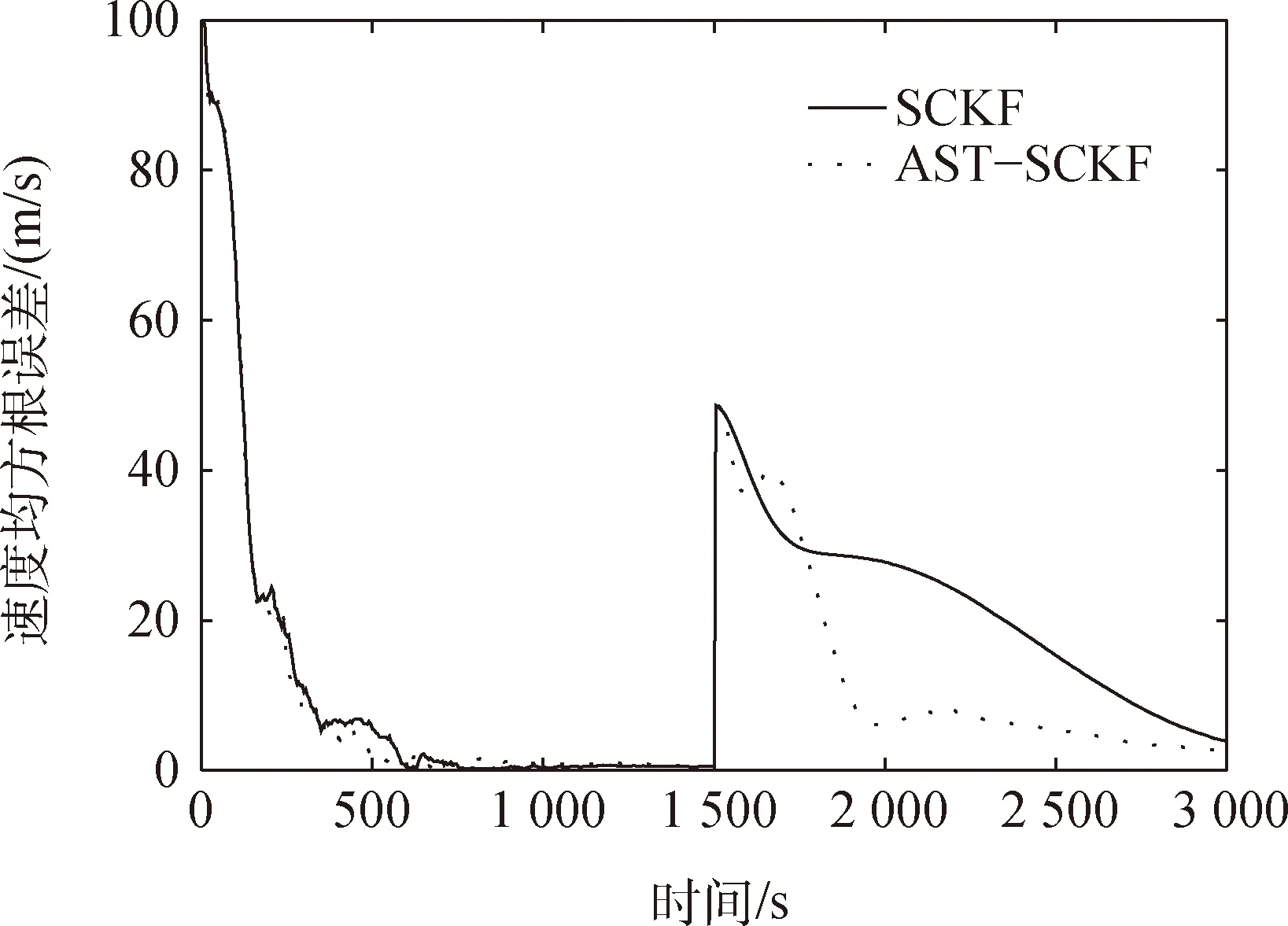
圖3 速度均方根誤差比較Fig.3 Comparison of velocity root-mean square error

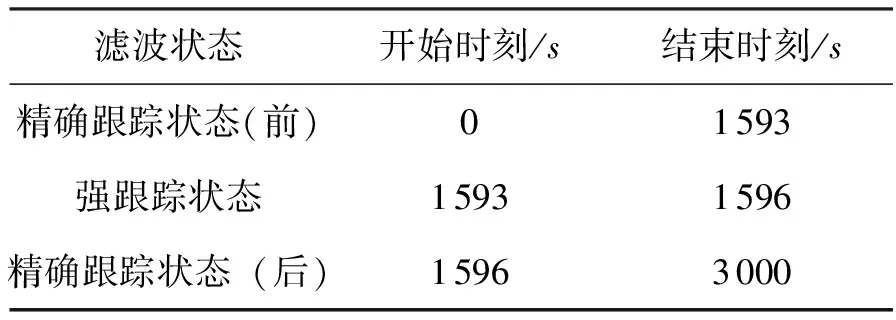
濾波狀態(tài)開始時刻/s結(jié)束時刻/s精確跟蹤狀態(tài)(前)01593強跟蹤狀態(tài)15931596精確跟蹤狀態(tài)(后)15963000

通過表1可以看出，在仿真開始時，濾波器處于精確跟蹤的狀態(tài)；目標(biāo)與1 500s機動后，濾波器在1 593s檢測到目標(biāo)機動，并自主切換到強跟蹤狀態(tài)，通過一個濾波周期(3s)的調(diào)整，迅速切換回精確跟蹤狀態(tài)，直至仿真結(jié)束。結(jié)果一方面表明了第2.2節(jié)中機動檢測機制的合理性，同時反映了AST-SCKF算法對濾波精確性和魯棒性的有效結(jié)合。

根據(jù)第3.3節(jié)中建立的性能指標(biāo)評價標(biāo)準(zhǔn)，對AST-SCKF算法和SCKF算法在目標(biāo)機動前后的跟蹤性能進行比較如表2和表3所示。

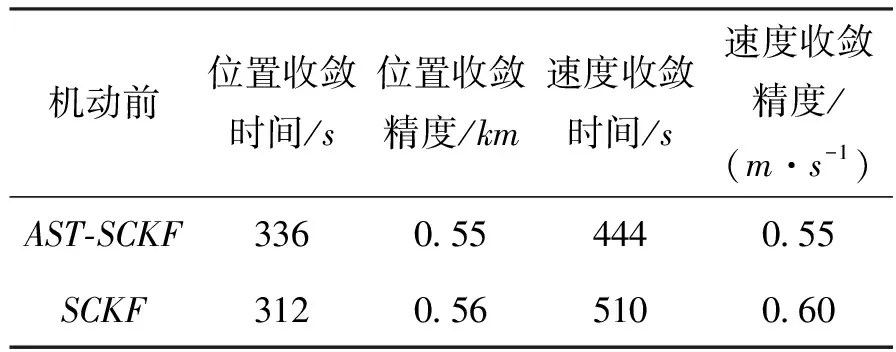
表2 目標(biāo)機動前SCKF與A-SCKF性能比較

仿真結(jié)果表明，在目標(biāo)機動前，AST-SCKF處于精確跟蹤狀態(tài)，AST-SCKF的位置收斂精度和速度收斂精度比SCKF算法分別提高了0.02%和8.33%，收斂速度分別提高了-0.75%和12.94%，顯示了機動前兩種算法的性能相當(dāng)；1 500s目標(biāo)發(fā)生機動造成目標(biāo)的狀態(tài)突變，SCKF濾波器出現(xiàn)嚴(yán)重的滯后，而AST-SCKF濾波器能在目標(biāo)機動后自適應(yīng)地切換至強跟蹤濾波狀態(tài)，從而在短時間內(nèi)再次精確跟蹤上目標(biāo)。

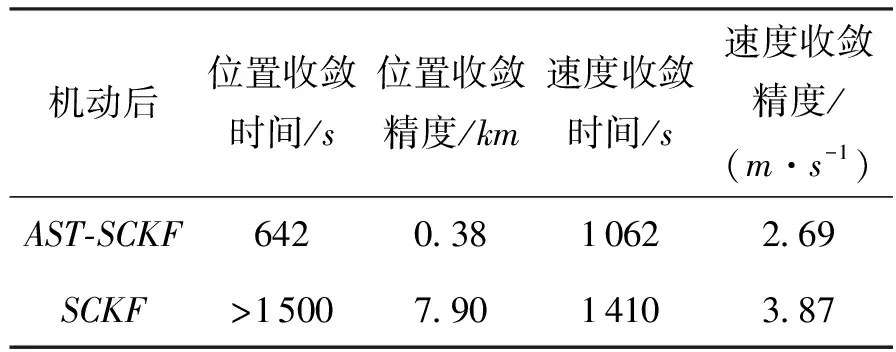
表3 目標(biāo)機動后SCKF與A-SCKF性能比較

AST-SCKF的位置收斂精度和速度收斂精度比SCKF算法分別提高了95.19%和30.50%，收斂速度分別提高了57.20%和24.68%，顯示了AST-SCKF算法的優(yōu)越性。

4 結(jié)束語

本文針對空間機動目標(biāo)跟蹤問題，主要工作和研究結(jié)論如下：

1)將STF次優(yōu)漸消的思想引入到SCKF中，并推導(dǎo)了次優(yōu)漸消因子在SCKF中的等價表達(dá)形式，突破了強跟蹤算法基于EKF的局限性，新的算法能在高階非線性濾波問題中得到較好的應(yīng)用，比如本文建立的考慮地球非球形攝動的空間目標(biāo)運動模型。

2)采用矩匹配的方法進行目標(biāo)機動檢驗，提出了一種檢測自適應(yīng)濾波方法——AST-SCKF算法，該算法能準(zhǔn)確檢測目標(biāo)的機動行為，并通過切換濾波狀態(tài)來達(dá)到濾波魯棒性和精確性的高度統(tǒng)一。但該檢測方式的閾值設(shè)置需要一定的先驗信息來輔助設(shè)置，不具備普遍性；另一方面當(dāng)前方法對機動行為的檢測仍存在一定的延遲現(xiàn)象。

3)通過仿真比較，驗證了本文算法在收斂時間和收斂精度上都明顯優(yōu)于傳統(tǒng)算法。但本文所研究的機動形式單一，而空間目標(biāo)的機動形式和機動能力都將不斷增強，因此，還需要對機動模型進行完善，同時研究能適應(yīng)多種機動形式的空間目標(biāo)的跟蹤算法。

References)

[1] 李冬，易東云，程洪瑋. 天基光學(xué)監(jiān)視的GEO空間目標(biāo)短弧段定軌方法J]. 中國空間科學(xué)技術(shù)，2011，31(3)：1-7.

LI D，YI D Y，CHENG H W. Orbit determination for GEO objects with short arcs of space-based optical observationsJ]. Chinese Space Science and Technology，2011，31(3)：1-7(in Chinese).

[2] LI X R，JILKOV V P. A survey of maneuvering target tracking-part II：Ballistic target modelsC]∥Proc. SPIE. 2001，4473：559-581.

[3] 周東華，席裕庚，張鐘俊. 非線性系統(tǒng)帶次優(yōu)漸消因子的擴展卡爾曼濾波J]. 控制與決策，1990(5)：1-6.

ZHOU D H，XI Y G，ZHANG Z J. Suboptimal fading extended Kalman filtering for nonlinear systemsJ]. Control and Decision，1990(5)：1-6(in Chinese).

[4] 周東華，席裕庚，張鐘俊. 一種帶多重次優(yōu)漸消因子的擴展卡爾曼濾波器J].自動化學(xué)報，199l，17(6)：689-695.

ZHOU D H，XI Y G，ZHANG Z J. A suboptimal multiple fading extended Kalman filterJ].Acta Automatica Sinica，199l，17(6)：689-695(in Chinese).

[5] 王小旭，趙琳，夏全喜，等. 基于Unscented變換的強跟蹤濾波器J]. 控制與決策，2010，25(7)：1063-1068.

WANG X X，ZHAO L，XIA Q X，et al. Strong tracking filter based on unscented transformationJ]. Control and Decision，2010，25(7)：1063-1068(in Chinese).

[6] 宋琛，韓潮，耿建中. 自適應(yīng)粒子濾波在紫外導(dǎo)航中的應(yīng)用J]. 中國空間科學(xué)技術(shù)，2009，29(1)：32-40.

SONG C，HAN C，GENG J Z. Application of adaptive particle filtering in ultraviolet sensorsJ]. Chinese Space Science and Technology，2009，29(1)：32-40(in Chinese).

[7] Uhlmann J，Julier S，Durrant-Whyte H F. A new method for the non linear transformation of means and covariances in filters and estimationsJ]. IEEE Transactions on Automatic Control，2000，45(3)：477-482．

[8] Arasaratnam I，Haykin S. Cubature Kalman smoothersJ]. Automatic，2011，47(8)：2245-2250.

[9] 潘泉，楊峰，葉亮，等. 一類非線性濾波器-UKF綜述J].控制與決策，2005，20(5)：481-489.

PAN Q，YANG F，YE L，et al. Survey of a kind of nonlinear filter—UKFJ]. Control and Decision，2005，20(5)：481-489(in Chinese).

[10] 郝燕玲，楊峻巍，陳亮，等. 平方根容積卡爾曼濾波器J]. 彈箭與制導(dǎo)學(xué)報，2012，32(2)：169-172.

HAO Y L，YANG J W，CHEN L，et al. Square root cubature Kalman filterJ]. Journal of Projectiles，Rockets，Missiles and Guidance，2012，32(2)：169-172(in Chinese).

[11] 涂文斌. 空間機動目標(biāo)跟蹤方法研究D]. 上海：上海交通大學(xué)，2012：65-85.

TU W B.Research on tracking of maneuvering spatial targetD]. Shanghai：Shanghai Jiao Tong University，2012：65-85. (in Chinese)

[12] 王志剛. 遠(yuǎn)程火箭與衛(wèi)星軌道力學(xué)基礎(chǔ)M].西安：西北工業(yè)大學(xué)出版社，2006：92-157.

WANG Z G. A long-range rocket and satellite orbital mechanicsM]. Xi′an：Northwest Polytechnical University Press, 2006：92-157(in Chinese).

[13] 李駿. 空間目標(biāo)天基光學(xué)監(jiān)視跟蹤關(guān)鍵技術(shù)研究D]. 長沙：國防科技大學(xué)，2009：65-95.

LI J. Research on key technologies of space objects surveillance and tracking in space-based optical surveillanceD]. Changsha：National University of Defense Technology，2009：65-95(in Chinese).

[14] 李恒年. 衛(wèi)星機動軌道確定M]. 北京：國防工業(yè)出版社,2013：75-95.

LI H N. Orbit determination for maneuvering satelliteM]. BeiJing：National Defense Industry Press, 2013：75-95(in Chinese).

[15] 劉也，劉磊，曹建峰，等. 單天基平臺測向的空間非合作目標(biāo)跟蹤J]. 飛行器測控學(xué)報，2014，33(4)：328-333.

LIU Y，LIU L，CAO J F，et al. Bearing-only tracking of non-cooperative space objects by a single space-based platformJ]. Journal of Spacecraft TT&C Technology，2014，33(4)：328-333(in Chinese).

[16] 林浩申，黃璜，劉剛，等. 基于SCKF算法的空間機動目標(biāo)跟蹤研究J]. 電光與控制，2015，22(3)：64-67.

LIN H S，HUANG H，LIU G，et al. Tracking of maneuvering spatial target based on SCKFJ]. Electornics Optics & Control，2015，22(3)：64-67(in Chinese).

(編輯：車曉玲)

A localization algorithm for adaptive maneuvering spatial targets

LIN Haoshen，LIU Gang*，HE Bing

RocketForceUniversityofEngineering，Xi′an710025，China

In the space target tracking problem，the model mismatch caused by target maneuvering leads to serious hysteresis. In order to track spatial target faster，the suboptimal fading parameter of strong tracking filter (STF) was introduced in square-root cubature Kalman filter (SCKF)，and the equivalent form was derived. On the basis of maneuvering detection，an adaptive strong tracking square-root cubature Kalman filter (AST-SCKF) which combined the accuracy and robustness was designed. The results of simulation show that the difference in positional accuracy between two algorithms is less than 1% before the maneuvering，but after the maneuvering，it turns out that the convergence accuracy of the AST-SCKF was 95.19% higher in position and 30.50% faster in velocity. Meanwhile，the convergence speed of AST-SCKF was 57.20% and 24.68% faster than SCKF in terms of position and velocity respectively.

spatial target localization；maneuvering target；bearing-only；adaptive filter；cubature Kalman filter；strong tracking filter; suboptimal fading parameter; maneuvering detection

10.16708/j.cnki.1000-758X.2017.0010

2016-05-04；

2016-07-28；錄用日期：2016-11-24；

時間：2017-02-16 16:46:20

http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1646.003.html

國家自然科學(xué)基金“基于量子生物地理優(yōu)化的低空UAV編隊在線協(xié)同航跡規(guī)劃方法研究”(61403399)

林浩申(1992-)，男，碩士研究生，linhaoshen1@163.com，研究方向為信息融合與目標(biāo)跟蹤

*通訊作者：劉剛(1964-)，男，教授，pdh_0818@163.com，研究方向為導(dǎo)航制導(dǎo)與控制

林浩申，劉剛，何兵. 自適應(yīng)空間機動目標(biāo)跟蹤算法J].中國空間科學(xué)技術(shù)，2017，37(1)：26-32.LINHS，LIUG，HEB.AlocalizationalgorithmforadaptivemaneuveringspatialtargetsJ].ChineseSpaceScienceandTechnology，2017，37(1)：26-32(inChinese).

P123.46

A

http:∥zgkj.cast.cn