矩形鋼管混凝土翼緣的H型蜂窩組合柱特征值屈曲性能

計 靜, 徐智超, 張文福,2, 沈 晶, 周利劍, 劉迎春, 盧召紅, 王濱洲

( 1. 東北石油大學 黑龍江省防災減災工程與防護工程高校重點實驗室，黑龍江 大慶 163318； 2. 南京工程學院 建筑工程學院，江蘇 南京 211167； 3. 大慶油田有限責任公司 第二采油廠，黑龍江 大慶 163414； 4. 中國石油天然氣股份有限公司 東北銷售分公司，遼寧 沈陽 110013 )

矩形鋼管混凝土翼緣的H型蜂窩組合柱特征值屈曲性能

計 靜1, 徐智超1, 張文福1,2, 沈 晶3, 周利劍1, 劉迎春1, 盧召紅1, 王濱洲4

( 1. 東北石油大學 黑龍江省防災減災工程與防護工程高校重點實驗室，黑龍江 大慶 163318； 2. 南京工程學院 建筑工程學院，江蘇 南京 211167； 3. 大慶油田有限責任公司 第二采油廠，黑龍江 大慶 163414； 4. 中國石油天然氣股份有限公司 東北銷售分公司，遼寧 沈陽 110013 )

為研究矩形鋼管混凝土翼緣的H型蜂窩組合柱(STHCC)穩定性能，以截面形式、約束條件、構件長度和混凝土強度等級為主要參數，設計11根不同截面形式的H型蜂窩鋼柱及18根 STHCC構件；基于構件的簡化力學模型和本構模型，利用ABAQUS有限元軟件建立29根試件的有限元模型，開展構件的特征值屈曲分析，將有限元數值解與實驗數據進行對比，兩者吻合較好，驗證有限元建模方法的合理性。基于18根STHCC構件特征值屈曲分析，提取變形云圖和屈曲荷載，考察屈曲荷載隨截面形式、構件長度、約束方式、混凝土強度等級和加勁肋的變化規律，給出STHCC在實際工程中的設計建議。結果表明： STHCC構件的整體穩定性比普通H型蜂窩鋼柱、鋼管翼緣的H型蜂窩鋼柱的好，在相同用鋼量條件下，屈曲荷載分別提高1.88、1.23倍；在STHCC構件鋼管翼緣內設置加勁肋后，屈曲荷載提高1.31倍，合理設置加勁肋可以大幅提高組合柱的整體穩定性。隨著混凝土強度等級的增加，構件屈曲荷載提高幅度越來越小。根據有限元數值解，通過簡化混凝土影響系數建立STHCC構件的屈曲荷載計算公式，獲得的屈曲模態為該類組合柱非線性穩定性能提供初始缺陷形態。

H型蜂窩組合柱； 鋼管混凝土； ABAQUS； 特征值屈曲； 屈曲荷載； 設計建議

0 引言

H型鋼柱具有質量輕、承載能力大、節約工時和造價低等優點，已被廣泛應用于工業與民用鋼結構體系。隨著建筑體系向超高、重載及大跨的方向發展，采用常規的鋼結構體系將形成胖柱，過多占用建筑空間，且鋼柱的穩定性問題突出，單一的鋼柱已不能很好地滿足結構體系需要。提出一種翼緣為鋼管混凝土的H型蜂窩組合柱(STHCC)，整體截面保持H型，翼緣采用鋼管混凝土的形式，混凝土可以防止鋼管發生局部屈曲；鋼管對混凝土可以產生連續約束效應，使混凝土處于三向受壓狀態。在翼緣雙肢鋼管混凝土之間采用蜂窩型腹板，不僅將獨立的雙肢柱有效地連接成為整體，而且可以大幅減輕組合柱的自重，具有剛度大且穩定承載力高的優點。

對翼緣采用空鋼管和鋼管混凝土的工字型鋼梁[1-3]的研究較多。任亞文[4]推導四種截面形式的矩形鋼管混凝土翼緣簡支梁彈性和塑性抗彎承載力理論計算公式。梁文峰[5]對上翼緣為矩形鋼管混凝土的工字型梁整體穩定承載力進行試驗研究，提出該類工字型梁正截面極限彎矩的計算公式。有關鋼管混凝土組合柱方面的研究多集中于常規的鋼管混凝土柱和格構柱。Akihiko Kawano[6]等對鋼管混凝土格構柱的抗震性能進行試驗研究，在鋼框架中加入鋼管混凝土格構柱，提出一種具有良好的抗震性能的新型抗震體系。Duan L[7]等研究格構柱的局部屈曲和整體屈曲性能，考慮初始缺陷的影響，給出該類鋼柱慣性矩的計算方法。Razdolsky A G[8]將格構柱視為超靜定構件，確定該類柱的換算長細比。根據穩定理論，鐘善桐[9]研究鋼管混凝土格構柱的穩定性，推導換算長細比的計算方法并給出穩定承載力計算公式。韓林海[10]開展50根鋼管—自密實混凝土短柱的軸壓性能試驗，提出該類柱的計算模型和簡化計算方法。Zhong Tao等[11]開展36根帶肋和不帶肋鋼管混凝土短柱的軸壓試驗，考察不同加勁肋布肋方式的影響，得出最優的截面形式。Han Linhai等[12]開展80根不同截面形式的雙層不銹鋼鋼管混凝土柱軸壓試驗，提出簡化計算公式和設計建議。陳寶春等[13]提出鋼管混凝土格構柱換算長細比的材料修正系數計算方法，給出四肢鋼管混凝土格構柱極限承載力計算公式。周婷[14]進行方鋼管混凝土組合異形柱軸壓、壓彎及擬靜力試驗研究，考察不同構造形式對組合異形柱承載力及抗震性能的影響，提出設計建議和計算方法。包博[15]推導鋼管混凝土格構柱的換算長細比，建立鋼管混凝土格構柱K形節點的承載力計算公式。

翼緣為矩形鋼管混凝土的H型蜂窩組合柱介于H型蜂窩鋼柱和雙肢鋼管混凝土格構柱之間，既具有雙肢鋼管混凝土格構柱的特征，又能表現出鋼柱的弱穩定性。對翼緣為矩形鋼管混凝土的H型蜂窩組合柱的研究較少，設計規程和方法也不完善。基于ABAQUS有限元軟件，筆者建立29個不同截面形式的H型蜂窩柱有限元模型，考察不同參數對該類組合柱屈曲荷載的影響規律，基于數值解回歸擬合該類組合柱的屈曲荷載計算公式，并給出設計建議。

1 試件設計

為研究翼緣為矩形鋼管混凝土H型蜂窩組合柱(STHCC)的穩定性能，以截面形式、約束方式、構件長度和混凝土強度等級為參數，設計29個試件，包括11根H型蜂窩鋼柱和18根翼緣為矩形鋼管混凝土的H型蜂窩組合柱；11根鋼柱中有8根鋼柱在翼緣矩形鋼管中布置加勁肋，試件參數及設計原則見表1，其中R-1、R-2和R-3分別表示試件約束方式為上端鉸接下端固接、上下兩端鉸接和上端自由下端固接。

根據GB 50017—2003《鋼結構設計規范》[16]，確定試件的計算長度。試件的16種截面形式見圖1。將所有試件鋼腹板開圓孔，形成蜂窩型腹板，孔高比d/hw取為0.7，距高比s/hw取為0.3，蜂窩型腹板開孔與未填充混凝土的空翼緣H型蜂窩組合柱截面尺寸變量的物理意義見圖2。以翼緣形式區分的三種截面形式S-2、S-3、S-14的立體試件見圖3。

2 組合柱有限元模型與驗證

2.1 力學計算模型

不同截面形式的29根翼緣H型蜂窩柱力學模型采用桿系模型，除試件C-20約束方式采用R-2、試件C-21約束方式采用R-3外，其他構件約束方式采用R-1。

2.2 鋼材和混凝土本構模型

鋼材采用Q235級鋼，彈性模量取為2.1×1011N/m2，采用雙線性本構模型。混凝土彈性模量按照文獻[18]選取，混凝土本構模型采用塑性損傷模型[18]。

2.3 有限元模型

采用ABAQUS有限元軟件[19]，建立不同截面形式的29個翼緣H型蜂窩柱的有限元模型。為考察鋼材和混凝土的應力分布，采用八結點六面體單元C3D8R模擬鋼板和混凝土。通過布置種子實現柱子的網格劃分。柱底約束所有節點的自由度(U1、U2、U3、UR1、UR2和UR3)以模擬固接；柱頂約束節點的水平和平面外位移(U1和U2)，豎向和轉角自由，以模擬鉸接；柱頂節點無約束以模擬自由端。軸向壓力以均布荷載方式施加于柱頂。試件C-3和C-14的有限元模型見圖4。

2.4 模型驗證

2.4.1 理論驗證

采用蜂窩型腹板時，鋼柱腹板的慣性矩降低，需要折減蜂窩型腹板的慣性矩，因此引入折減因數ky(折減后與折減前腹板截面慣性矩之比)。蜂窩型腹板折減因數ky與d/hw、s/hw相關，根據試驗獲得折減因數公式[20]，求出鋼柱的等效慣性矩，代入歐拉公式即可求出不同截面形式的H型蜂窩鋼柱的彈性屈曲荷載理論解。開展不同截面形式的H型蜂窩鋼柱特征值屈曲數值分析，將獲得的特征值系數乘以柱頂荷載即可得到試件的屈曲荷載。采用不同網格劃分的4個試件，保持截面形式不變，擴展不同長細比的構件在不同網格尺寸下的屈曲分析，屈曲荷載數值解與理論解的結果見圖5。由圖5可知，在網格尺寸劃分為0.04 m時，有限元數值解與理論解吻合較好。11個試件(C-1-C-11)的彈性屈曲荷載數值解(見表2)，與其理論解吻合較好，可見采用精細網格劃分后，不同截面形式的H型蜂窩鋼柱有限元建模是正確合理的。

表1 試件主要參數與設計原則

注：/表示試件未涉及該項，加勁肋為矩形且截面尺寸為16 mm×40 mm。

圖1 試件的橫截面類型及具體尺寸(單位:mm)Fig.1 The cross section type and specific dimension of specimens (unit: mm)

圖2 蜂窩型腹板與空翼緣H型鋼柱截面示意Fig.2 The schematic diagram of the honeycomb shaped web and the section of H type steel column with hollow flange

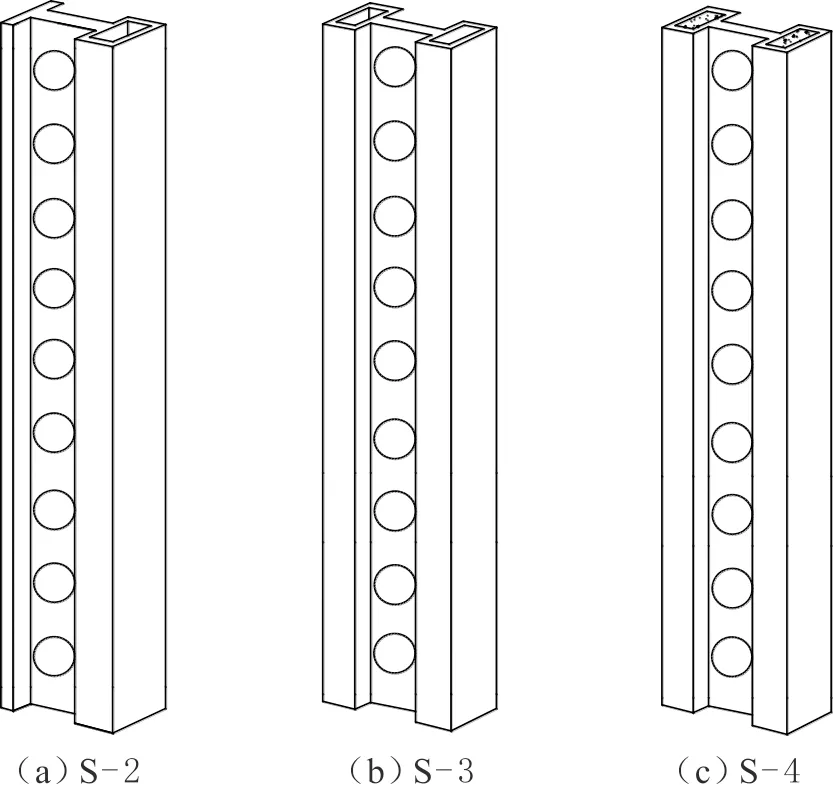
圖3 以翼緣區分的三種截面立體試件Fig.3 The stereoscopic specimens of three kinds of sectional forms distinguished by flanges

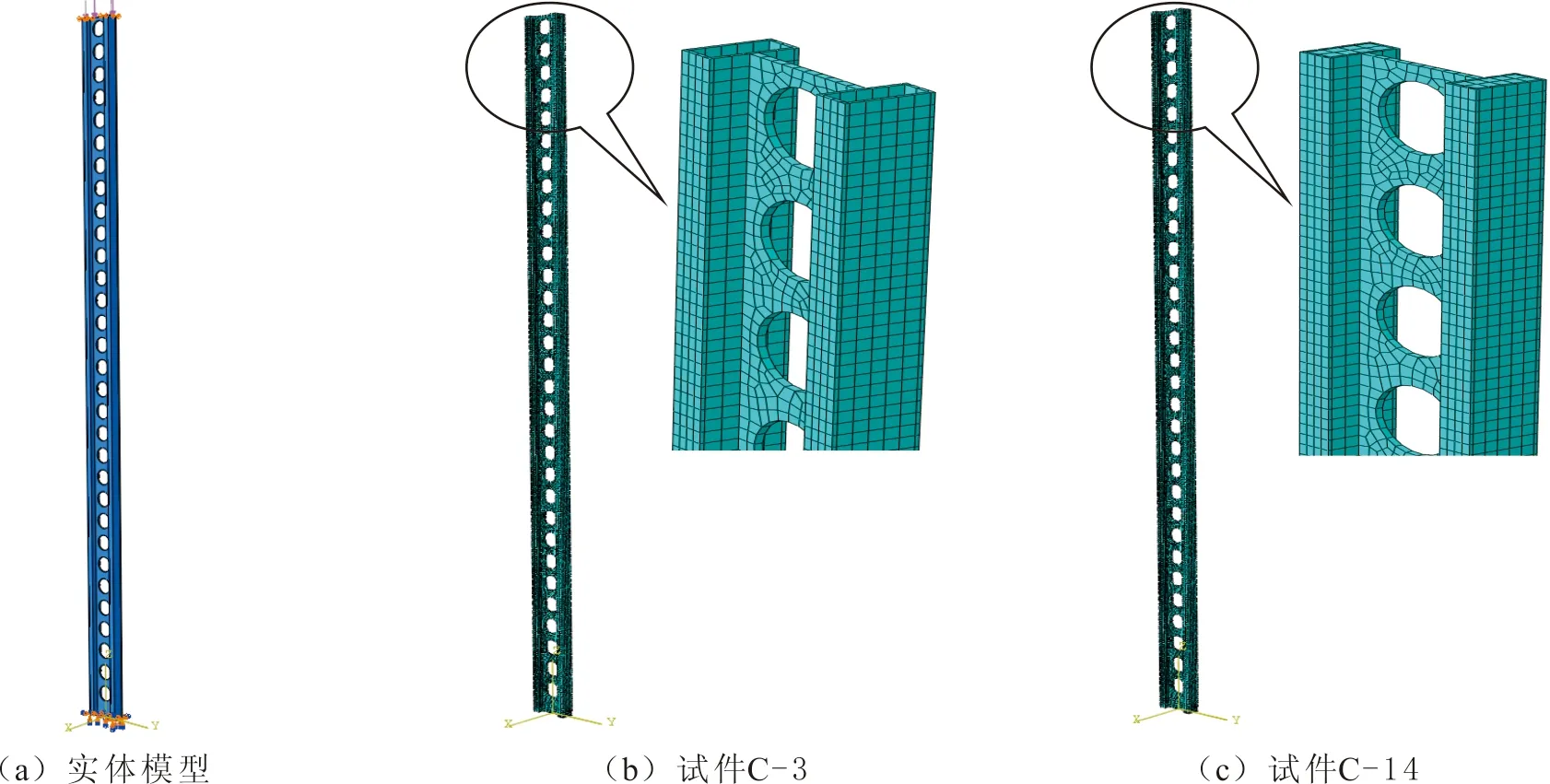
圖4 試件C-3和C-14的有限元模型Fig.4 The finite element model of specimen C-3 and C-14

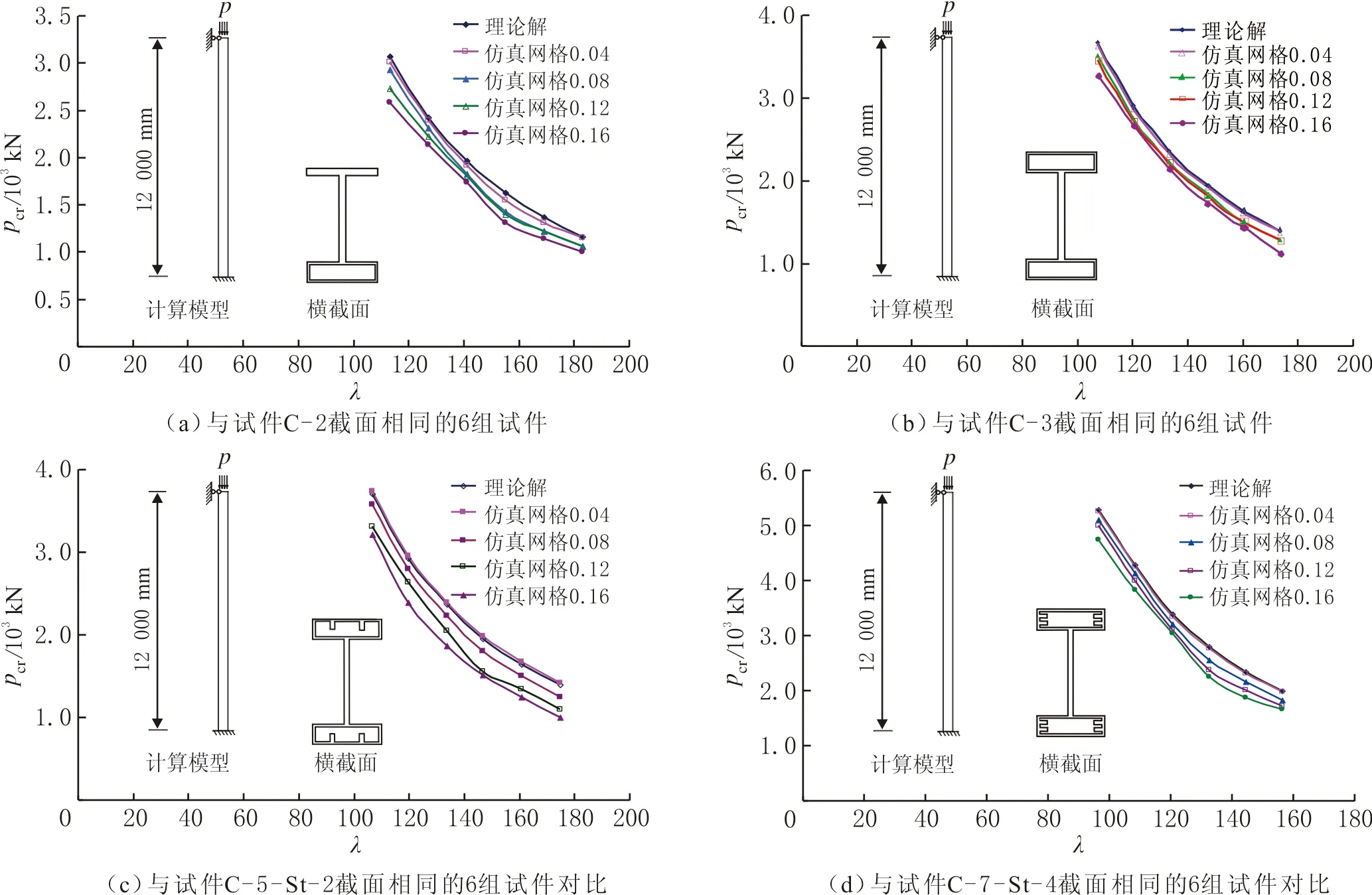
圖5 不同網格劃分的4個試件屈曲載荷有限元數值解與理論解Fig.5 Comparison between finite element simulation solution and theoretical solution

編號截面積A/m2慣性矩Iy/m4回轉半徑i/m長細比λ理論解pTcr/kN數值解pScr/kN|pTcr-pScr|/pScrC?118．80×10-33．75×10-50．0446188109910504．7%C?218．80×10-34．66×10-50．0498169136813114．3%C?318．80×10-35．57×10-50．0525160163416051．8%C?4?St?120．08×10-35．59×10-50．0527159164016611．3%C?5?St?221．36×10-35．63×10-50．0514163165116842．0%C?6?St?321．36×10-36．82×10-50．0565149200119741．4%C?7?St?423．92×10-38．08×10-50．0581145237123391．4%C?8?St?518．80×10-35．51×10-50．0551153161716371．2%C?9?St?618．80×10-35．60×10-50．0564149164216721．8%C?10?St?718．80×10-36．80×10-50．0593142199519681．4%C?11?St?818．80×10-37．11×10-50．0637132208620591．3%

2.4.2 實驗驗證

按照文中建模方法，對文獻[21]的11根鋼管混凝土長柱進行數值屈曲分析，構件參數及實驗獲得的穩定承載力Nue見表3，鋼管與混凝土之間的粘結滑移對屈曲荷載影響較小，故未考慮混凝土與鋼管之間的粘結滑移作用。在特征值屈曲分析的基礎上，考慮試件的初始缺陷，進行非線性屈曲分析，獲得的特征值屈曲Nuse及非線性屈曲Nusn仿真結果見表3。特征值屈曲和非線性屈曲仿真結果與實驗結果的偏差圖見圖6。由表3和圖9可以看出，有限元屈曲仿真值與實驗值總體上吻合較好，采用文中建模方法開展鋼管混凝土柱的屈曲分析是可行的，由于翼緣為矩形鋼管混凝土H型蜂窩組合柱與鋼管混凝土柱類似，可以采用相同的建模方法開展穩定承載力分析。

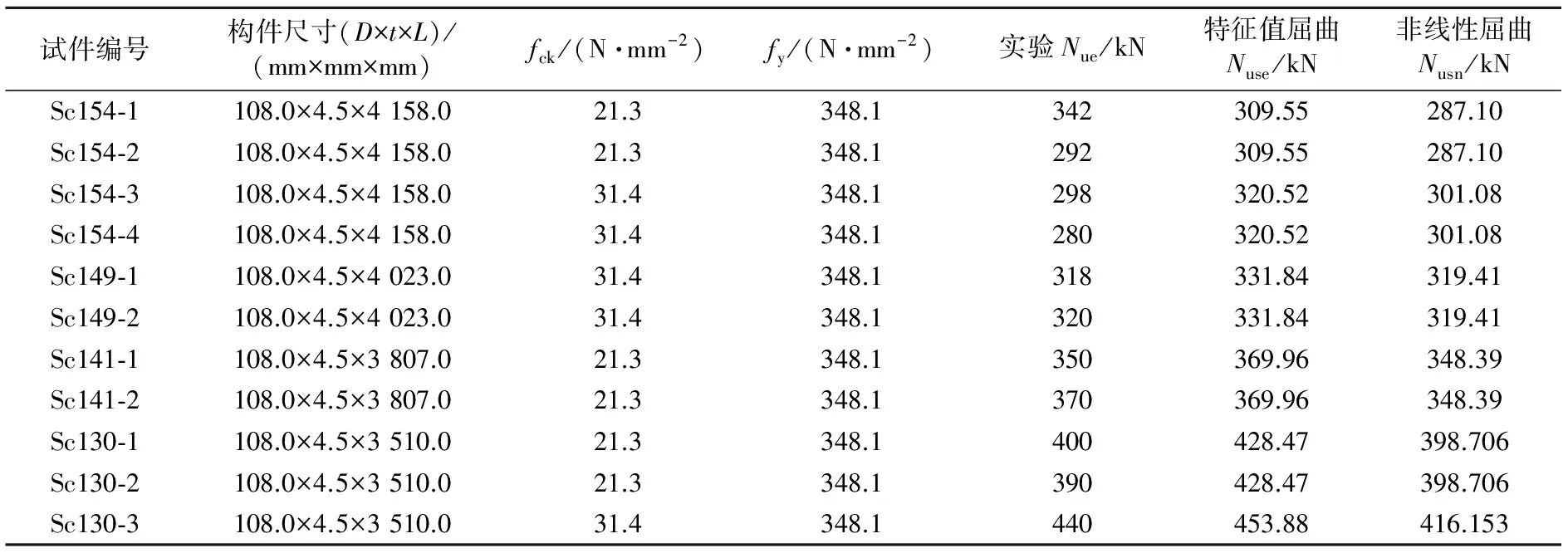
表3 11個軸壓長柱試件參數及穩定承載力

注：fck為混凝土軸心抗壓強度標準值；fy為鋼材屈服強度

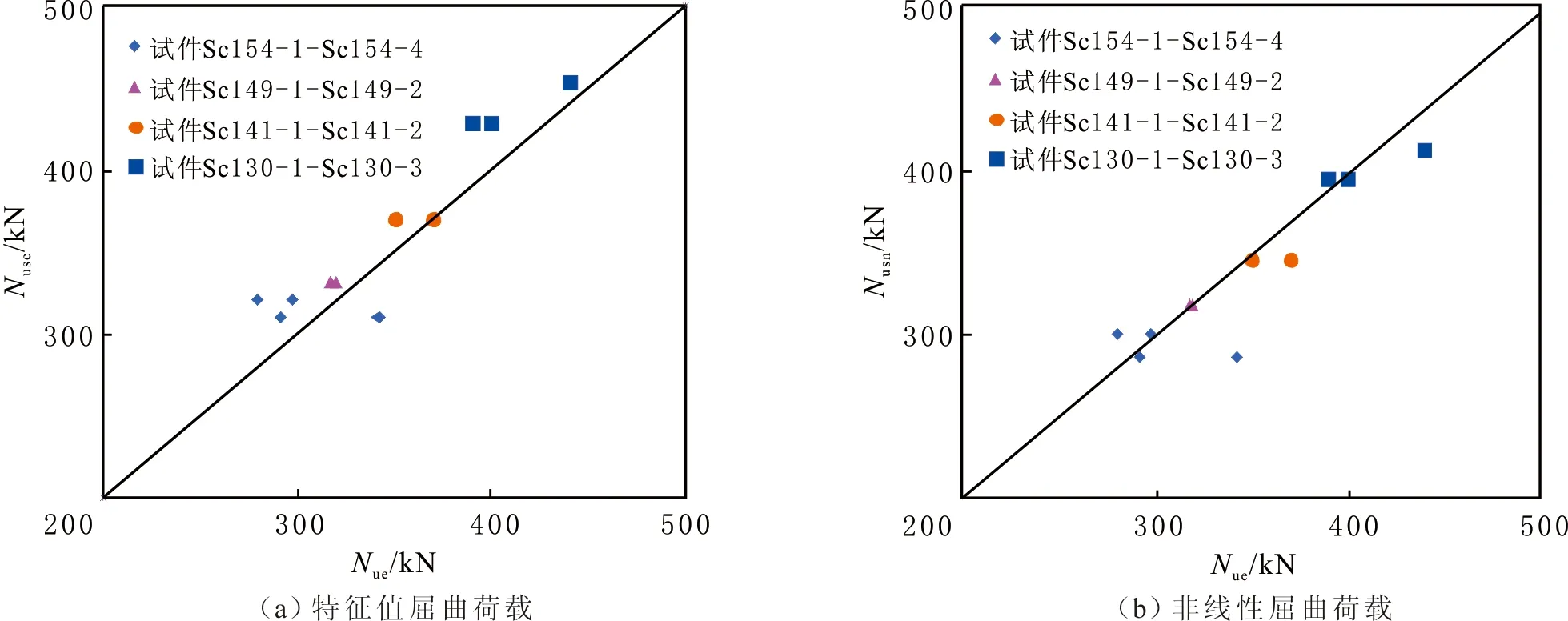
圖6 11個試件屈曲仿真值與試驗值Fig.6 Comparison between simulation value and test value of 11 groups of specimens

3 STHCC構件整體穩定性

3.1 截面形式

表4 三種截面形式構件屈曲荷載數值解

Table 4 The numerical solution of buckling load of components with three kinds of sections

試件編號截面形式數值解/kNC?12S?121513C?13S?131779C?14S?141969

在保證截面鋼材面積不變的情況下，對三種截面形式的STHCC構件開展特征值屈曲分析。不同截面形式的STHCC屈曲分析變形云圖見圖7，其中試件C-12和C-13截面形式為非對稱的，變形主要表現為彎扭屈曲；試件C-14為彎曲屈曲，獲得的屈曲荷載數值解見表4。由表4可以看出，在保證截面鋼面積不變的情況下，試件翼緣截面由鋼板到鋼管，再演變到鋼管混凝土，屈曲荷載分別提高17.6%和30.1%，在翼緣矩形鋼管內添加混凝土，可以大幅提高翼緣的穩定性，從而使組合柱的穩定性能明顯提高。

圖7 三種截面形式的STHCC構件變形云圖Fig.7 Deformation cloud image of three kinds of STHCC specimens

3.2 長度

在保證各構件橫截面形式(采用S-14截面形式)和材料相同的條件下，對不同長度的STHCC(上端鉸接下端固接)進行屈曲分析，獲得的變形云圖見圖8，構件變形表現為彎曲屈曲。獲得的屈曲荷載數值解見表5。

圖8 不同長度的STHCC試件變形云圖Fig.8 Deformation cloud image of STHCC specimens with different length

Table 5 The numerical solution of buckling load of components with different lengths

試件編號實際長度數值解/kNC?158．04417C?169．03493C?1710．02831C?1811．02341C?1412．01969C?1913．01678

由圖8可以看出，由于構件底部是固結，在底部附近出現反彎點，過了反彎點構件的變形呈現正弦半波的形式。由表5可以看出，隨著試件長度的增加，試件整體穩定屈曲荷載數值解逐漸減小；當長度由8.0 m增加到13.0 m時，屈曲荷載減少62.0%，長度對于構件屈曲荷載的影響較大。

3.3 約束方式

對長為12 m的三種不同約束方式的STHCC構件進行屈曲分析，獲得的變形云圖見圖9，構件變形為彎曲屈曲。獲得的屈曲荷載數值解見表6。

圖9 不同約束方式的STHCC構件變形云圖

Table 6 The numerical solution of buckling load of components with different constraint modes

試件編號約束方式數值解/kNC?14R?11969C?20R?2964C?21R?3240

由圖9和圖7(c)可以看出，R-1約束方式的構件底部是固結，在底部附近出現反彎點，過了反彎點構件變形呈現正弦半波的形式；R-2約束方式的試件兩端是鉸接，端部彎矩值為零，變形為完整的正弦半波的形式；R-3約束方式的試件屬于懸臂構件，為彎曲變形且柱端的彎矩最大。盡管長度相同，但約束方式不同，導致柱的實際計算長度相差很大。對于12.0 m的柱子，計算長度分別為8.4、12.0和24.0 m，屈曲荷載值相差較大。

圖10 不同混凝土強度等級的STHCC構件變形云圖Fig.10 Deformation cloud image of STHCC specimen with different concrete strength grades

3.4 混凝土強度等級

在保證各構件橫截面形式(采用S-14截面形式)和材料相同的條件下，對不同混凝土強度等級的STHCC構件進行特征值屈曲分析，獲得的變形云圖見圖10，構件變形為彎曲屈曲。獲得的屈曲荷載數值解見表7。

由圖10和表7可以看出，在翼緣鋼管內添加混凝土可以提高柱子的整體穩定性，隨著混凝土強度等級的提高，試件屈曲荷載逐漸增加。從C40增加到C80時，屈曲荷載由1 948 kN增加到2005 kN，增加2.9%，可見混凝土強度的增加對屈曲荷載的改善是有限的；因為混凝土的彈性模量變化不大，導致對截面慣性矩的影響不大。

表7 不同混凝土強度等級試件屈曲荷載數值解

Table 7 The numerical solution of buckling load of components with different strength grades of concrete

試件編號混凝土強度等級數值解/kNC?22C201875C?23C301922C?24C401948C?14C501969C?25C601984C?26C701995C?27C802005

3.5 加勁肋形式

對不同加勁肋形式的STHCC構件(C-28和C-29)進行特征值屈曲分析，獲得的變形云圖見圖11，構件變形為彎曲屈曲。獲得的屈曲荷載數值解見表8。

由圖11和表8可以看出，在帶有加勁肋的翼緣鋼管內添加混凝土，可以大幅提高組合柱的整體穩定性，加勁肋和混凝土對截面慣性矩起到雙重的作用，比任何一種單一布置的屈曲荷載都大。

3.6 試件屈曲荷載分析

11個不同截面形式的H型蜂窩鋼柱試件和11個翼緣為鋼管混凝土的H型蜂窩組合柱試件屈曲荷載見圖12。22個試件約束方式和長度相同。翼緣為鋼管的試件C-3填充混凝土后形成試件C-14，根據虛線1，屈曲荷載由1 605 kN增加到1 969 kN，提高22.7%。翼緣為鋼管的試件C-3增加加勁肋后形成試件C-7-St-4，屈曲荷載由1 605 kN增加到2 339 kN，比試件C-14屈曲荷載提高18.8%。在保持面積不變的情況下,翼緣為鋼管的試件C-3通過減小腹板厚度轉換成加勁肋而形成C-11-St-8構件，屈曲荷載與翼緣為鋼管混凝土的試件基本相同(見虛線2)。在試件C-7-St-4的基礎上，翼緣鋼管添加混凝土后形成試件C-29，屈曲荷載由2 339 kN增加到2 588 kN，提高10.6%，可見在翼緣鋼管內設置與弱軸方向垂直的加勁肋對構件的穩定性起重要作用。

圖11 不同加勁肋形式的STHCC構件變形云圖

Table 8 The numerical solution of buckling load of components with different stiffening ribs

試件編號帶加勁肋的截面形式數值解/kNC?28S?152285C?29S?162588

圖12 22個試件屈曲荷載Fig.12 Comparison of buckling loads for 22 specimens

4 H型蜂窩組合柱屈曲荷載

由于翼緣為鋼管混凝土的H型蜂窩柱作為一種新型的組合柱，還沒有相關規范和規程給出屈曲荷載計算公式。根據該類組合柱的屈曲荷載有限元數值解，建立屈曲荷載計算公式。該類組合柱截面由鋼管和混凝土構成，采用單一鋼截面計算慣性矩不再適用，根據剛度相等的原則將混凝土轉換成鋼材，通過引入因數β，建立截面的等效慣性矩：

(1)

圖13 因數β與屈曲荷載的關系Fig.13 The relationship between coefficient β with buckling load

參考歐拉公式，明確試件的約束條件和屈曲荷載，反推截面的等效慣性距Iq，進而確定因數β。16個試件(C-14-C-29)的因數β與屈曲荷載pcr之間的關系見圖13。

由圖13可以看出，擬合后的曲線變化微小，基本趨近水平線，β=0.896 0。翼緣為鋼管混凝土的H型蜂窩組合柱彈性屈曲荷載計算公式為

(2)

(3)

式(1-3)中：Es、Ec分別為鋼材和混凝土的彈性模量;μ為構件計算長度系數;l為構件的實際長度;Iq為截面的等效慣性矩;ky為腹板慣性矩折減系數[20]；Is、Ic分別為鋼材和混凝土的慣性矩；其他變量含義見圖2。

5 結論

(1)以截面形式、約束條件、構件長度、混凝土強度等級為主要參數，設計11根不同截面形式的H型蜂窩鋼柱及18根翼緣為矩形鋼管混凝土的H型蜂窩組合柱(STHCC)，考察屈曲荷載隨截面形式、構件長度、約束方式、混凝土強度等級和加勁肋的變化規律，參考歐拉公式建立STHCC構件的屈曲荷載計算公式。

(2)在翼緣為矩形空鋼管的H型蜂窩鋼柱的空鋼管內增加與腹板方向垂直的加勁肋后，屈曲荷載可以提高1.46倍；在相同用鋼量條件下，屈曲荷載可以提高1.28倍。STHCC構件的整體穩定性比普通H型蜂窩鋼柱和翼緣為鋼管的H型蜂窩鋼柱的好，在相同用鋼量條件下，與后兩者相比屈曲荷載分別提高1.88倍、1.23倍。在STHCC構件翼緣鋼管內設置與腹板方向垂直的加勁肋后，屈曲荷載提高1.31倍。隨著混凝土強度等級的增加，構件屈曲荷載提高的幅度越來越小。

(3)在實際工程中，框架角柱和內柱應制做成截面對稱的，可以將翼緣為矩形鋼管混凝土的H型柱腹板做成十字型，形成翼緣為矩形鋼管混凝土的十字型組合柱，從而大幅提高柱子的雙向整體穩定性和承載能力。

[1] Wilkinson T, Judd M, Popplewell M, et al. Bearing capacity of hollow flange beams with web penetrations [C]. Hongkong: 13th International Symposium on Tubular Structures, 2010.

[2] Tharmarajah Anapayan, Mahen Mahendran. Improved design rules for hollow flange sections subject to lateral distortional buckling [J]. Thin-Walled Structures, 2012,50(1):128-140.

[3] Hassanein M F, Kharoob O F, El Hadidy A M. Lateral-tensional buckling of hollow tubular flange plate girders with slender stiffened webs [J]. Thin-Walled Structures, 2013,65(2):49-61.

[4] 任亞文.矩形鋼管翼緣梁抗彎性能的試驗與理論研究[D].大慶:東北石油大學,2015. Ren Yawen. Experimental and theoretical investigation of bending behavior for rectangular steel tube flange beams [D]. Daqing: Northeast Petroleum University, 2015.

[5] 梁文峰.上翼緣為矩形鋼管混凝土工字形梁的整體穩定承載力試驗研究[D].大慶:東北石油大學,2016. Liang Wenfeng. Experimental research on global stability behavior of I-beams with top flange of rectangular concrete-filled steel tube [D]. Daqing: Northeast Petroleum University, 2016.

[6] Akihiko Kawano, Chiaki Matsui. Cyclic local buckling and fracture of concrete filled tubular members [C]. Banff: Proceedings of the Conference: Composite Construction in Steel and Concrete IV, 2000:632-643.

[7] Duan L, Reno M, Uang C. Effect of compound buckling on compression strength of built-up members [J]. Engineering Journal, 2002,39(1):30-37.

[8] Razdolsky A G. Flexural buckling of laced column with crosswise lattice [J]. Proceedings of the ICE-Engineering and Computational Mechanics, 2008,161(2):69-76.

[9] 鐘善桐.鋼管混凝土結構[M].北京:清華大學出版社,2010. Zhong Shantong. The concrete-filled steel tubular structures [M]. Beijing: Tsinghua University Press, 2010.

[10] Han Linhai, Yao Guohuang, Zhao Xiaoling. Tests and calculations for hollow structural steel(HSS) stub columns filled with self-consolidating concrete(SCC) [J]. Journal of Constructional Steel Research, 2005,61(9):1241-1269.

[11] Zhong Tao, Han Linhai, Wang Dongye. Strength and ductility of stiffened thin-walled hollow steel structural stub columns filled with concrete [J]. Thin Walled Structures, 2008,46(10):1113-1128.

[12] Han Linhai, Ren Qingxi, Li Wei. Tests on stub stainless steel-concrete-carbon steel double-skin tubular(DST) columns [J]. Journal of Constructional Steel Research, 2011,67(3):437-452.

[13] 陳寶春,歐智菁.鋼管混凝土格構柱極限承載力計算方法研究[J].土木工程學報,2008,41(1):55-63. Chen Baochun, Ou Zhijing. Calculation method for the ultimate load carrying capacity of concrete-filled steel tubular lattice columns[J].China Civil Engineering Journal, 2008,41(1):55-63.

[14] 周婷.方鋼管混凝土組合異形柱結構力學性能與工程應用研究[D].天津:天津大學,2012. Zhou Ting. Mechanical behavior and engineering application of special-shaped column composed of concrete-filled square steel tubes [D]. Tianjin: Tianjin University, 2012.

[15] 包博.鋼管混凝土格構柱力學性能研究[D].哈爾濱:哈爾濱工業大學,2013. Bao Bo. Research on the mechanical property of concrete filled steel tubular laced column [D]. Harbin: Harbin Institute of Technology, 2013.

[16] GB 50017—2003,鋼結構設計規范[S]. 北京:中國建筑工業出版社,2003. GB 50017—2003, Code for design of steel structures [S]. Beijing: China Building Industry Press, 2003.

[17] Key P W, Hancock G J. A theoretical investigation of the column behavior of cold-formed square hollow section[J]. Thin-Walled Structures 1993,16(1):31-64.

[18] 劉威.鋼管混凝土局部受壓時的工作機理研究[D].福州:福州大學,2005. Liu Wei. Research on mechanism of concrete-filled steel tubes subjected to local compression [D]. Fuzhou: Fuzhou University, 2005.

[19] 王玉鐲,傅傳國.ABAQUS結構工程分析及實例詳解[M].北京:中國建筑工業出版社,2010. Wang Yuzhuo, Fu Chuanguo. ABAQUS structural engineering analysis and detailed examples [M]. Beijing: China Architecture & Building Press, 2010.

[20] 張益凡.蜂窩梁的整體和局部穩定分析[D].長沙:中南大學,2008. Zhang Yifan. Global and local stability analysis of cellular beams [D]. Changsha: Central South University, 2008.

[21] 韓林海.鋼管混凝土結構:理論與實踐[M].北京:科學出版社,2007. Han Linhai. Concrete-filled steel tubular structures: Theory and practice [M]. Beijing: Science Press, 2007.

2016-12-16；編輯：任志平

教育部高等學校博士學科點專項科研基金項目(新教師類：20122322120004)；國家自然科學基金項目(51178087)；黑龍江省自然科學基金面上項目(E201336)；黑龍江省級領軍人才梯隊后備帶頭人資助(RCHB-6)；中國石油科技創新基金項目(2016D-5007-0608)；國家自然科學基金東北石油大學校培育基金項目(NEPUPY-1-16，NEPUQN2014-25)；東北石油大學校級研究生創新科研項目(YJSCX2016-031NEPU)；黑龍江省教育廳科研專項經費東北石油大學優勢科研方向凝練基金項目(2016YSFX-02)

計 靜(1977-)，男，博士，教授，主要從事土木結構工程方面的研究。

TU324.5

A

2095-4107(2017)01-0106-11

DOI 10.3969/j.issn.2095-4107.2017.01.011