激光移除空間碎片過程的三維仿真與建模

張品亮，龔自正，楊武霖，陳 川

( 北京衛星環境工程研究所, 北京100094)

激光移除空間碎片過程的三維仿真與建模

張品亮，龔自正，楊武霖，陳 川

( 北京衛星環境工程研究所, 北京100094)

基于軌道力學和激光與物質相互作用理論建立激光移除空間碎片的三維變軌模型。該模型利用激光站/衛星與碎片位置和速度矢量作為初始數據，通過設定激光參數，實時計算和更新速度增量矢量，能夠真實地反映碎片的移除過程。該模型包括地基和天基兩種類型，根據激光作用臨界條件與降軌效果計算碎片的降軌過程，能夠實時輸出碎片軌道信息，圖形化輸出使結果更加直觀。考慮到速度增量分量對軌道傾角的影響，該模型增加了碎片逃逸情況的判斷。最后，利用該模型計算了地基/天基系統移除多種空間碎片材料的過程和效果，發現鋼材料碎片移除難度最大，而移除多層絕緣材料的效率最高。

激光燒蝕；空間碎片；變軌；三維仿真；數值模型

0 引 言

日益嚴峻的空間碎片環境，對航天器的安全運行造成嚴重威脅，減緩空間碎片的數量是空間技術發展面臨的關鍵問題。近年來，以NASA和ESA為代表的航天組織對空間碎片移除技術進行了探索，提出了多種移除方法[1-5]。其中激光移除碎片技術具有獨特的優勢，是國際上一致認可的理想碎片移除方法，它具有操作簡單、效率高、響應時間短和成本較低等優點。該技術的基本原理是：當高強度脈沖激光照射在碎片表面時，使表面材料等離子化產生高溫氣體，產生一系列類似于火箭反推的熱物質反噴羽流，給碎片提供速度增量來降低近地點高度，使其在較短時間內落入大氣層燒毀，達到移除空間碎片的目的。

激光移除碎片系統可分為地基[6]和天基[7]兩種類型，它們各有優缺點。地基系統成本較低，維護方便，能量轉化成本低，但是對碎片的監測時間受光照影響，并且容易受到大氣干擾，效率較低。而天基系統可以實現全天監視，移除效率高，但維護困難，能源使用成本高。

從二十世紀末期開始，航天強國就已經開始激光移除碎片的技術論證。NASA將這個項目命名為ORION[8-9]。這項研究采用地基激光系統，主要針對高度在400～1100km的危險空間碎片。ESA也開展了激光移除空間碎片的計劃CLEANSPACE[10]，該項目將建立一個從空間碎片環境監測、跟蹤、識別到激光移除的系統框架。此外，中國學者也對空間碎片的監測[11]、定軌[12]和姿態跟蹤導航[13]，以及激光與物質相互作用[14]、地基/天基驅動碎片變軌規律[14]等問題進行了研究。

無論地基還是天基，在激光移除碎片進程中，碎片的降軌是關鍵問題之一。目前已經建立了一些理論模型來計算碎片的變軌過程[14-15]，雖然這些模型可以定性地反映速度增量與降軌效果的關系;但是，它們以固定的速度增量作為初始數據[16]，而與激光物質相互作用分離開來，這樣在計算中就忽略了碎片移動過程中速度增量的變化。此外，這些模型大部分為二維模型，假設激光與碎片軌道在同一平面上，而忽略了軌道傾角變化對速度增量的影響。因此，研究一種具有普適性的、應用更加靈活的三維模型對定量分析激光移除空間碎片的過程具有重要意義。

針對以上問題，本文基于軌道力學和激光與物質相互作用相關理論建立了三維變軌模型。該模型包括地基和天基兩種類型，根據輸入的激光和碎片相關參數，計算成功移除碎片所需的脈沖數量和作用過程，并且實現了圖形化輸出。

1 三維變軌模型

在三維空間的變軌問題中，根據地心赤道坐標系中碎片的初始位置和速度矢量，以及激光站的位置矢量，激光的波長、頻率等參數，計算模擬空間碎片的降軌過程。

首先需要判斷碎片是否具有移除條件，即：碎片的位置是否在激光的作用范圍內。如果不在作用范圍內，碎片按照脈沖時間間隔t開始移動，直到碎片進入激光作用范圍內，開始計算脈沖激光與碎片的相互作用。依據相互作用機理，計算單次激光脈沖作用后碎片的狀態矢量，得到變軌后碎片的軌道根數，判斷激光脈沖作用后碎片軌道近地點高度是否降低，如果降低則使激光脈沖作用次數+1，更新變軌后碎片狀態矢量；反則不作用，保持原軌道狀態矢量。隨后開始下一脈沖時間間隔t碎片狀態的判斷和計算，確定碎片的位置和速度矢量。以t為單位重復計算，直到近地點高度小于設定值(即移除成功)，或者碎片超出激光作用范圍。對于后者，根據碎片的移動，重新判斷碎片是否具有移除條件，開始二次或多次過頂/交會計算直到碎片被移除，或者逃逸出具備移除條件的軌道，無法繼續移除。圖1為模型的計算流程圖。

1.1 軌道根數的確定

在地心赤道坐標系中，X軸指向春分點的方向，XY平面為地球的赤道平面，Z軸與地球的旋轉軸一致，且指向北。單位矢量i、j和k滿足右手定則。在給定時刻，空間碎片的初始狀態向量速度v0和位置r0，在地心赤道坐標系中狀態向量可表示為：

r0=x0i+y0j+z0k

(1)

v0=vx0i+vy0j+vz0k

(2)

在該點受到激光輻照后，獲得速度增量

Δv=Δvxi+Δvyj+Δvzk

(3)

變軌后速度矢量和位置矢量分別為：

v=v0+Δv=(vx0+Δvx)i+

(vy0+Δvy)j+(vz0+Δvz)k

(4)

r=r0

(5)

根據二體運動方程和牛頓定律可以計算出變軌后的軌道根數[12]：比角動量的模h、軌道傾角i、升交點赤經Ω、偏心率e、近地點幅角ω和真近點角θ。

1.2 軌道與時間的函數

如果已知t0時刻的位置r0和速度v0，其模分別為r0和v0。可由拉格朗日系數f和g及其一階導數，根據下述表達式求出任意時刻的位置r和速度v：

r=fr0+gv0

(6)

(7)

利用全局變量χ和斯達姆夫函數C(z)與S(z)所表示的拉格朗日系數如下：

(8)

(9)

(10)

(11)

其中長半軸的導數α為：

(12)

對于橢圓軌道，α>0。

如果已知Δt、r0、v0和α，可從全局開普勒方程中解出全局近點角χ，具體步驟如下：

計算χ0合理的初始估計值：

(13)

以χ0為初始數據進行迭代計算：

(14)

(15)

其中vr0為v0在r0方向上的投影,vr0=(r0·v0)/r0。

(16)

(17)

(18)

算出比值ηi=f(χi)/f′(χi)。如果|ηi|超出精度范圍10-8，則按χi+1=χi-ηi重新選取χ估計值，計算式(14)、(15)直到|ηi|<10-8，則接受χi作為解。這樣就可以根據式(6)、(8)、(9)得到Δt時刻的位置矢量r，根據式(7)、 (10) 、(11)得到Δt時刻的速度矢量v[17]。

1.3 判定激光作用條件

在地基移除系統中，由于受到大氣的影響，理論上只有當天頂角在-45°～45°范圍內才能使從地面發射的激光輻照在空間碎片上[18]。但是在計算中，向量夾角的范圍在0～180°，需要根據碎片的坐標和象限來計算天頂角，特別是對于任意激光站位置和空間碎片軌道的情況，這無疑增加了計算的復雜程度。本文采用激光站地表切面的方法，對是否具備移除條件進行判斷。

假設激光站坐標為 (x0,y0,z0), 碎片的位置矢量為(x1,y1,z1)，地球球面方程為：x2+y2+z2=63782，根據幾何方法可確定激光站點在地球表面的切面方程：x0x+y0y+z0z=63782。

只有在碎片移動到激光站上方時(x1x0+y1y0+z1z0-63782>0)，才具有移除條件，此時向量夾角即為天頂角。這樣就可對碎片的天頂角進行精確判斷，而無需考慮碎片和激光站的象限問題。

在天基系統中，可根據碎片與激光衛星的距離來判斷是否具有移除條件。本文認定300km為激光的作用范圍。

當碎片進入作用范圍后，需要判斷是否適合進行激光輻照，如果作用后近地點高度降低則進行輻照，反則不輻照，碎片繼續按原軌道移動，繼續判斷下一個脈沖的作用效果。

1.4 激光與碎片相互作用

激光輻照物體表面時，產生反噴沖量，使物體獲得速度增量，沖量耦合系數反映了激光能量轉化為物體沖量的能力。在確定速度增量時，激光與材料的沖量耦合系數是主要參數：

Cm=pτ/Φ=mΔv/E

(19)

其中，激光作用后靶的質量m=m0-μE；μ為激光燒蝕率(鋁為80×10-9kg/J[18])；p為一個強度為I、脈寬τ的激光脈沖在靶上產生的燒蝕壓；激光通量為Ф；E為靶上的激光能量。目前已經通過實驗獲得了多種材料的Cm值[19-20]。

為了在較大距離上將激光傳輸到靶上，需要數千焦的激光脈沖能量和大型發射鏡來克服光的衍射：

(20)

ds=aM2λz/Deff

(21)

式中：ds為靶上光斑直徑，M2為光束質量因子(≥1，1代表最好)，Deff為計算衍射時輸出孔徑D中的有效照射光直徑，a為一個乘數因子，對于高斯光束a=4/π。對于一個從地基系統發出的高斯光束，修正后光束質量M2=2.0，Deff/D=0.9，a=1.7[19]。

如果需要將通量為Ф的激光輻照到距離為z的靶上，激光器需要輸出WD2的激光[21]，

(22)

式中：W為激光脈沖能量，Teff為有效傳輸率。

研究表明[22]：不同形狀的空間碎片在相同的激光脈沖下所獲得的速度增量可能不同。對于激光輻照球體材料，所獲得的沖量為垂直輻照平板材料的2/3[23]。在計算模型中，對激光輻照次數進行記錄，每次輻照后碎片的質量變化都能夠計算，從而獲得精確的速度增量。

1.5 碎片逃逸

在三維軌道計算中，速度增量可能與碎片軌道不在同一個平面上，這樣就會產生速度增量改變碎片的軌道傾角，當軌道傾角增加到一定程度時，碎片就逃逸出激光的作用范圍，無法繼續作用。在地基系統中，如果碎片沿當前軌道移動一周后仍然不具備激光輻照的條件，則認為碎片逃逸。在天基系統中，如果激光與碎片在100個軌道周期內不交會，則碎片逃逸。

2 計算實例

在地基系統中，本文采用波長為1.06μm的近紅外激光，具體參數列于表1中，分別采用了1mm、1cm和10cm三種直徑的球形鋁碎片進行計算，初始軌道參數列于表1中。墜入大氣層燒毀的判據為近地點高度≤200km[9]。

表1 地基激光系統和空間碎片相關參數

計算結果表明，碎片的初始位置不在激光的作用范圍內。碎片移動4145.54s后，在位置(-5852.6,-3837.3,2361.7)處進入激光作用范圍(此時天頂角為45°)。表2為計算結果，結果表明：對于具有相同軌道參數、材質、形狀和姿態的碎片，隨著碎片直徑的增加，移除所需要的時間增加，過頂次數增加。在本文的算例中，對于1mm的碎片，能夠利用394次脈沖在一次過頂中被移除；而10cm的碎片，則需要19次過頂39636次脈沖，經歷154172s才能被移除。采用100kW左右的激光裝置，能在2～3天、19次過頂之內移除0.1～10cm的碎片。表3為移除過程中關鍵點的實時信息。圖2(a)為圖形化輸出結果，其中黑色圓點為激光站位置，灰色圓點為碎片初次變軌位置。

表2 激光移除碎片所需的過頂/交會次數，脈沖次數和時間

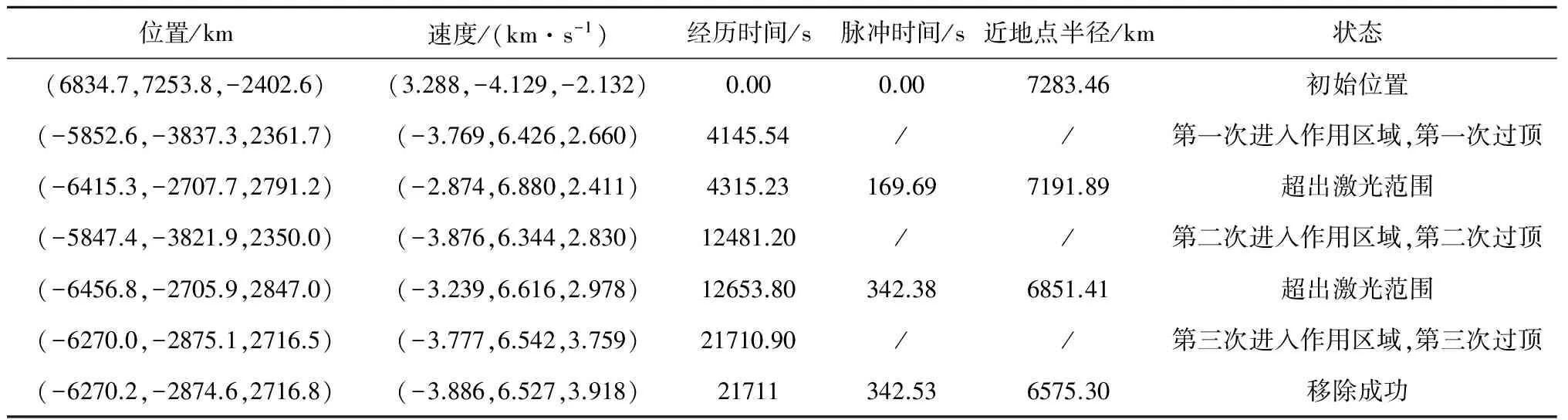
表3 直徑1cm碎片的移除過程(地基)

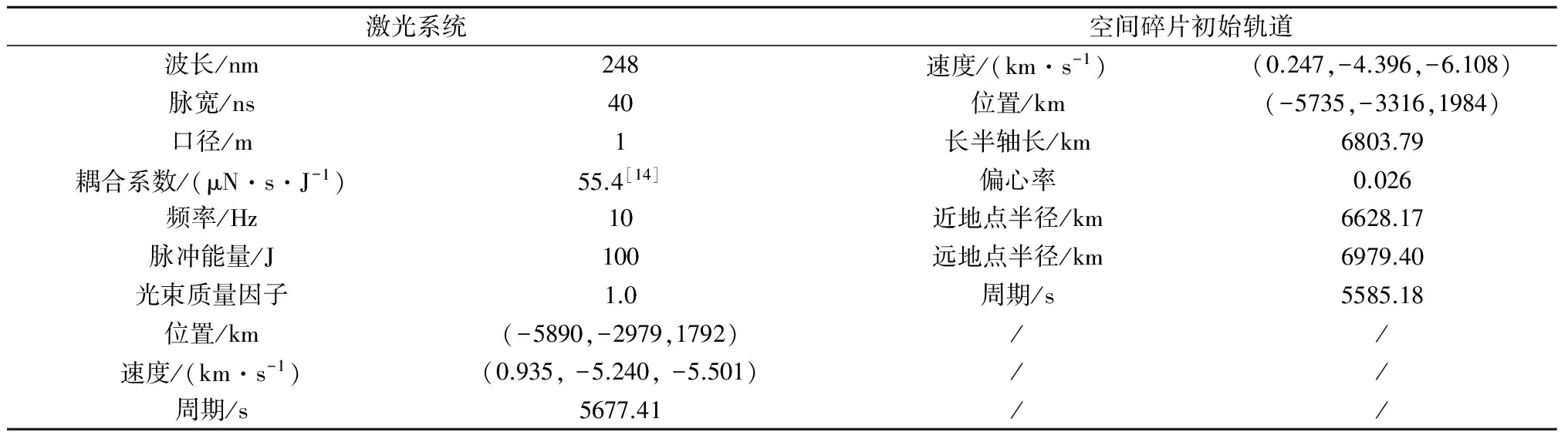
表4 天基激光系統和碎片初始軌道參數

在天基系統中，我們采用波長為248nm的近紫外激光，激光衛星和空間碎片的初始軌道參數見表4，其中耦合系數來源于文獻[19]。結果表明：碎片的初始位置不在激光的作用范圍內，經過143.7 s，碎片在位置(-5678.3, -3722.3, 1383.1)處進入激光(-5765.3, -3467.9, 1250.0)作用范圍(此時距離為300km)。計算結果列于表2，對于具有相同初始狀態的碎片，隨著碎片直徑的增加，移除所需要的時間增加，交會次數增加。在本文的算例中，采用1kW的激光裝置，在一次交會中就能移除1 cm的碎片，對于較大碎片需要多次交會。天基所需激光系統功率遠低于地基系統，移除效率明顯高于后者。圖2(b)為移除1 cm碎片的圖形化輸出結果。

3 常見空間碎片的移除效果

在Orion項目中[8]將空間碎片分為5大類：Na/K冷卻劑、碳酚醛樹脂、多層絕緣材料(MLI)、鋁和鋼。不同的材料具有不同的移除效果，本文計算了這些常見空間碎片的移除過程，碎片參數取自文獻[9]。假設激光始終垂直輻照在全部截面上，計算結果見表5。可以發現鋼材料的移除難度最大，多層絕緣材料最容易被移除。本文算例中，對于天基系統，利用表4中的激光參數，能夠移除所有碎片。對于地基，利用110.5kW的激光裝置，能夠移除除鋼材料之外的全部碎片。在三維空間中，由于速度增量不一定在碎片軌道平面上，向外的速度分量使軌道傾角增大，在多脈沖長時間作用下使碎片逃逸出激光站的作用范圍，無法達到移除碎片的目的。因此，在實際操作中應選擇合適的作用位置和激光脈沖參數。

從表5可以看出，天基系統對激光系統的功率需求遠小于地基系統，天基1kW的激光能夠在三次交會中移除所有碎片，獲得優于地基110.5kW的移除效果，并且移除效率遠遠高于后者。

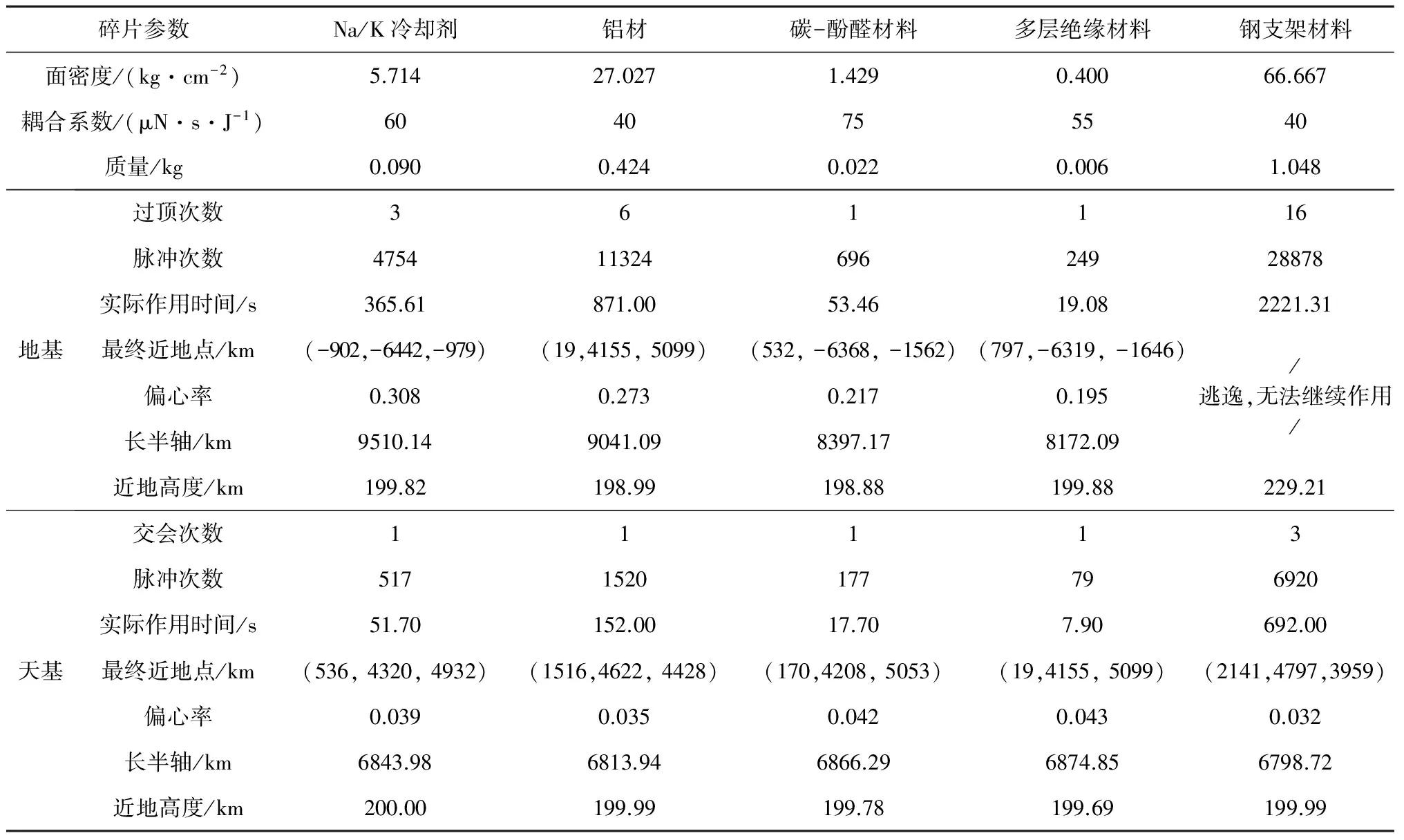
表5 地基和天基系統移除5種常見空間碎片的效果

4 結 論

本文建立了適用于地基和天基激光移除空間碎片系統的三維仿真模型。該模型能夠根據輸入的激光(能量、頻率、波長、位置矢量等)和碎片參數(耦合系數，位置矢量，速度矢量等)，計算碎片的變軌過程，實時輸出碎片的軌道信息和移除結果。

采用該模型計算了波長為1.06μm的近紅外地基系統和波長為246nm的近紫外天基系統移除碎片的過程。結果表明：天基系統對激光系統的功率需求遠小于地基系統。在本文的算例中，采用100kW左右的地基激光裝置，能在2～3天、19次過頂之內移除給定軌道上0.1～10cm的鋁碎片。采用1kW的天基激光裝置，在一次交會中就能移除給定軌道上1cm的鋁碎片，對于較大碎片需要多次交會。不同材料具有不同的移除效果，其中鋼材料的移除難度最大，多層絕緣材料最容易被移除。由于存在軌道傾角，向外的速度增量分量使軌道傾角增大，在多脈沖的作用下可能使碎片逃逸出激光站/衛星的作用范圍。

[1] Weeden B. Overview of the legal and policy challenges of orbital debris removal [J]. Space Policy, 2011, 27(1): 38-43.

[2] White A E, Lewis H G. The many futures of active debris removal [J]. Acta Astronautica, 2014, 95: 189-197.

[3] Levin E, Pearson J, Carroll J. Wholesale debris removal from LEO [J]. Acta Astronautica, 2012, 73: 100-108.

[4] 陳欽, 楊樂平. 空間繩網系統發射動力學問題研究[J]. 宇航學報, 2009，30(5): 1829-1833. [Chen Qin, Yang Le-ping. Research on casting dynamics of orbital net systems [J]. Journal of Astronautics, 2009, 30(5): 1829-1833.]

[5] 劉志新, 游秀楊, 洪玖, 等. 基于擴張狀態觀測器的空間飛網捕捉系統參數估計[J]. 宇航學報, 2014, 35(2): 906-915. [Liu Zhi-xin，You Xiu-yang，Hong Jiu，et al. The Parameter estimation based on extended state observerfor space net capture system [J]. Journal of Astronautics, 2014, 35(2): 906-915.]

[6] Phipps C R, Baker K L, Libby S B, et al. A laser optical system to remove low Earth orbit space debris[C]. Sixth European Conference on Space Debris, Darmstadt, Germany, April 22-25, 2013.

[7] Choi S H, Pappa R S. Assessment study of small space debris removal by laser satellites [C]. 2011 IEEE Aerospace Conference, Montana, USA, March 5-12, 2011.

[8] Campbell J W. Project ORION: orbital debris removal using ground-based sensors and lasers [R]. NASA Technical Memorandum 108522, 1996.

[9] Phipps C R, Friedman H, Gavel D, et al. ORION: clearing near-Earth space debris using a 20 kW, 530 nm Earth-based, repetitively pulsed laser [J]. Laser Particle Beams, 1996, 14(1): 1-44.

[10] Esmiller B, Jacquelard C. CLEANSPACE “Small debris removal by laser illumination and complementary technologies”[J]. AIP Conference Proceedings, 2011, 1402(1): 347.

[11] 袁振濤, 胡衛東, 郁文賢. 電子籬笆型空間監視雷達測向數據關聯算法[J]. 宇航學報, 2009, 30(5): 1972-1978. [Yuan Zhen-tao, Hu Wei-dong, Yu Wen-xian. Direction data association in NAVSPASUR-type space surveillance radar[J]. Journal of Astronautics, 2009, 30(5): 1972-1978.]

[12] 李冬, 易東云, 程洪瑋. 天基空間目標監視的短弧段定軌技術[J]. 宇航學報, 2011, 32(11): 2339-2345. [Li Dong, Yi Dong-yun, Cheng Hong-wei. Orbit determination with short arcs for space-based space object surveillance [J]. Journal of Astronautics, 2011, 32(11): 2339-2345.]

[13] 翟光, 張景瑞. 空間非合作目標快速姿態跟蹤導航方法研究[J]. 宇航學報, 2013, 34(3): 362-368. [Zhai Guang, Zhang Jing-rui. Research on rapid attitude tracking for space non-cooperative target [J]. Journal of Astronautics, 2013, 34(3): 362-368.]

[14] 常浩, 金星, 洪延姬, 等. 地基激光清除空間碎片過程建模與仿真[J]. 航空學報, 2012, 33(6): 994-1001. [Chang Hao, Jin Xing, Hong Yan-ji, et al. Modeling and simulation on ground-based lasers cleaning space debris [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 994-1001.]

[15] Rubenchik A M, Erlandson A C, Liedahl D. Laser system for space debris cleaning [J]. AIP Conference Proceedings, 2012, 1464(1): 448-455.

[16] Phipps C R, Baker K L, Libby S B, et al. Removing orbital debris with lasers [J]. Advances in Space Research, 2012, 49: 1283-1300.

[17] Curtis H D. Review of orbital mechanics for engineering students [J]. Journal of Guidance, Control, and Dynamics, 2008, 21(2): 445-446.

[18] 洪延姬, 金星. 激光清除空間碎片方法[M]. 國防工業出版社, 2013.

[19] Phipps C. An alternate treatment of the vapor-plasma transition [J]. International Journal of Aerospace Innovations, 2011, 3(1): 45-50.

[20] Phipps C, Turner T P, Harrison R F, et al. Spicochi. Impulse coupling to targets in vacuum by KrF, HF and CO2 lasers [J]. J. Appl. Phys., 1988, 64(3): 1083-1096.

[21] Phipps C R. A laser-optical system to re-enter or lower low Earth orbit space debris [J]. Acta Astronautica, 2014, 93: 418-429.

[22] Liedahl D A, Libby S B, Rubenchik A. Momentum transfer by laser ablation of irregularly shaped space debris [J]. AIP Conf. Proc., 2010, 1278(1): 772-779.

[23] 金星, 常浩, 洪延姬, 等. 激光輻照不規則空間碎片沖量矢量計算[J].強激光與粒子束, 2012, 24(8):1956-1960. [Jin Xing, Chang Hao, Hong Yan-ji, et al. Impulse calculation for irregularly shaped space debris under laser irradiation[J]. High Power Laser and Particle Beams, 2012, 24(8): 1956-1960.]

通信地址：北京市海淀區友誼路104號(100094)

電話：(010)68745870

E-mail:zhangpinliang620@126.com

(編輯：牛苗苗)

Three-Dimensional Simulation and Modeling on Removing Orbital Debris with Lasers

ZHANG Pin-liang, GONG Zi-zheng, YANG Wu-lin, CHEN Chuan

(Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

This paper establishes a laser irradiation three-dimensional orbit dynamic model based on the theory of orbital mechanics and the interaction effects between laser and matters. With the position vector and velocity vector regarded as the initial data, and setting the parameters of laser, this model calculates the velocity and provides the real-time updates, which can actually reflect the process of the debris removal. It contains the ground-based and space-based models, both of them can output the orbit information of the debris real-time updates, and the graphical output directly displays the process of the orbital transfer. The effect of the velocity increment component on the orbit inclination is taken into consideration, thus this model can deal with the situation of the debris escape. Moreover, we successfully calculate the removal process and the result of various debris using ground-/space-based model. We suppose that it is the most difficult to remove steel, while multilayered insulation removal is the most efficient.

Laser ablation; Space debris; Orbital transfer; 3D simulation; Numerical model

2016-11-14;

2017-01-12

V416.5; TN249

A

1000-1328(2017)03-0323-08

10.3873/j.issn.1000-1328.2017.03.014

張品亮(1986-)，男，博士，工程師，主要從事航天器空間碎片防護、空間碎片移除、材料動態力學性能和高壓物理等研究。