行“通融”之徑進“無痕”之境
許貽亮

“無痕,是教育的至高境界。”怎樣的教育是無痕教育?筆者基于無痕教育的理念,在教學實踐中提出并踐行了“通融數學”——行“通融”之徑,進“無痕”之境。
“通融”是兩個詞語的疊加,其一為“通”,其二為“融”。通,心理學上類似于“順應”,在“順應中求通”,從而明白到“原來是這樣啊!”“通”含有:通俗、通道、直通、通透、變通等之義。融,心理學上類似于“同化”,在“同化中求融”,從而感悟到“它們是一樣的!”“融”含有:融合、融洽、融和、融化、融通等之義。其根源在于無痕教育,追求的是在教學中“有情有理,有法有度”,讓一切教學資源“自然和諧”,從而達成不露痕跡、重劍無鋒、潤物無聲的無痕境界。
中醫上說,“通則不痛,痛則不通”,想通了、理通了,學習就水到渠成了。如教學物體的運動方式“旋轉”時,“順時針”怎樣讓學生通透地理解?如果我們反復地強調“像時針、分針那樣旋轉的方向就是順時針”,這樣便要求學生理解并掌握“順時針”就顯得有點無理了。如果教師能夠用簡單、通俗的數學語言,簡潔易懂地說清其數學本質,通透的理解就可達成。譬如,借用鐘面上的12個數字,其中12既是終點又是起點,還可以看作0,從而就形成了一個有序的等差數列:0、1、2、3、4、5、6……如是觀之,當旋轉時經過的區域對應的數字是從小到大的,即為順時針,反之即為逆時針。這樣就“通”了,無需死記硬背,學生自然可感悟到“原來是這樣啊!”這樣教學,進入了潛移默化中理解的“無痕”之境。
與此同時,教者應有廣闊的教學視野,生活與數學、現代與古代、數學與其他學科、知識的前世今生未來等無一不是教學的優質資源。如果能縱觀全局,聚零為整,融多為一,那么產生的價值將大大超過“1+1=2”。如教學《比例的認識》時,可以問學生:“比例,我們今天剛學,它是全新的知識還是以往就學過的舊知識?”幫助學生梳理知識之間的聯系,可以感知到其和商不變規律、分數的基本性質、比的基本性質等“形變質不變”。
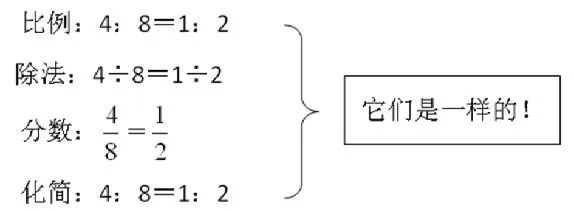
這樣,學生在不知不覺中思考、分析、對比,便無縫地融入原有的認知結構中,體會到數學之間豐富的聯系,感悟到“變中不變”的數學思想,達成春風化雨中提升數學能力的“無痕”效果。
“有之以為利,無之以為用。”“通融”與“無痕”是“目與綱”的關系,綱舉目張;“通融”與“無痕”是“枝與根”的關系,根深枝茂;“通融”與“無痕”是“形與神”的關系,神足形備。下面,以北師大版五年級上冊《分數的再認識》一課為例,展開來談。
一、通融之間應不露痕跡
讓學習在“不知不覺中開展”是無痕教育的實踐策略之一。如何做到?通俗與融合可以做到。通俗,就是低起點,能夠讓學生無聲中感到親切。融合,就是巧蘊蓄,能夠讓學生不露痕跡地思考、深入。
教學中,在先簡單地回顧三年級學過的分數內容:把誰平均分?平均分幾份?取了多少份?怎么讀?怎么寫?怎么算?接著,逐次出示如下教學素材:
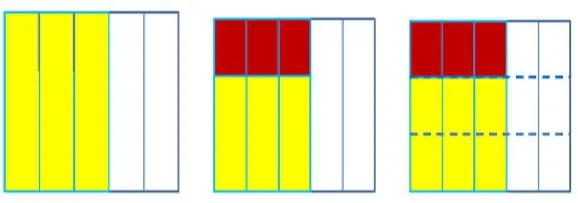
第1圖,屬于舊知的范疇;第2圖,就屬于新知的領域,這時涂色的部分占了整個長方形的幾分之幾?是八分之三、十一分之三、十五分之三?學生在觀察與思考中展開“變通”之旅:畫輔助線,一條不夠,再畫一條,如第3圖。這里,素材是通俗的:長方形;問題是通俗的:陰影部分占幾分之幾?但在這通俗之中,先“分”再“數”,“分數,先分一分,再數一數”的理解與感悟卻在不知不覺中展開,既淺顯易懂又深刻到位。這樣教學,比糾結于“一個整體”有幾種情況?“若干份”是什么意思?等更有教學的價值。
二、通融之間應重劍無鋒
讓學習“在循序漸進中掌握”是無痕教育的實踐策略之一。如何做到?通透與融化可以做到。通透,就是看得清,能夠讓學生破除認知中的迷障;融化,就是化得了,能夠把新知融入原有認知結構之中。
如本教學單元中,有著關于“大于1的分數”的認識,這是教學的難點。其難在于,學生在三年級學習分數的初步認識之后,其思維中關于分數也就有了個不完善的“前概念”,以為“等于1的分數”已經是最大的分數了,因此“大于1的分數”難以理喻。在教學中,我以數軸為載體,讓學生思考:“往下數是幾?”
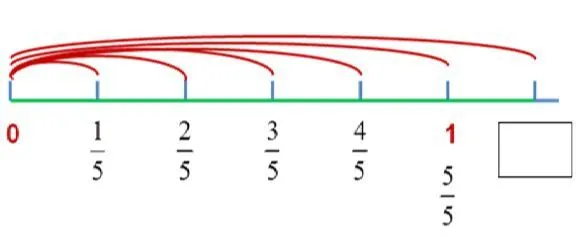
教學中,退到學生的已有舊知和思維起點,從一份數起,再一份一份地累加。道生一、一生二、二生三、三生萬物。從已經是最大的”認知冰點到“分數也可以無限大”的思維熱點,再把分數的數、整數的數、小數的數融在一起,感悟其中的“同”:它們是一樣的!認知就這樣在對話中無聲無息地達成。
三、通融之間應潤物無聲
讓學習“春風化雨中提升”是無痕教育的實踐策略之一。如何做到?變通與融通可以做到。變通,就是會活學,能夠讓學生具體問題具體分析;融通,就是會活用,能夠讓學生彼此相連,融會貫通。
如教學“兩個未知的整體,比較取相同分率或不同分率的部分,無法確定”。我們提供怎樣的教學素材合適些?——誰取的乒乓球多?
方案一:

方案二:

如果采取方案一,學生常滯于物,囿于兩個兩箱可見的大小關系,常問的問題是“第一個箱子里面可以放幾個第二個箱子?”難以跳出具象的思維全方位地考量三種不同情況。而采取方案二,則學生常能頓悟出:“都有可能!”甚至會“小大人”的口吻道:“不知道,別亂說!”從比較兩個已知整體到比較兩個未知整體,從確定性思維到不確定性思維,挑戰的是學生的分析、想象、推理等數學素養。教學中,改變的只是把第二個小箱子換成一個集合圖,便能夠幫助學生跳出認知的誤區,教學中,學生多數人第一反應都是“第二個箱子取出的乒乓球多大于在有人質疑的情況下,變通之旅隨之展開,通過舉例知道也有可能第二個箱子取出來的多。這時,可以引導思考:“怎么兩種想法都對呢?”明白本題的獨特性“未知的兩個整體”,讓學生經由“同化”“順應”再到認知“平衡”。不自見,故明;不自是,故彰。教學中,一問一疑一導,教師似乎只是在穿針引線,沒有做鮮明的強調或教學,而學習于此就潤物無聲地達成了。“處無為之事,行不言之教。”折射出來的是“真水無香”的無痕追求。
無痕教育,言有盡而意無窮。在實踐中、在思考中、在研究中,越是前行,對于前方的風景就越是期待。

