多樣情境 多元表征 多維考量
——《分數的初步認識》教學案例(一)
陳 瑾
【教學內容】
人教版三年級上冊第90、91頁。
【課前思考】
分數的初步認識是在學生認識了萬以內的數、掌握平均分和倍的知識的基礎上進行的教學。分數的認識分為兩個學段來教學:三年級上冊主要是借助操作和直觀,從“部分——整體”的角度初步認識分數;五年級下冊則是在此基礎上使學生從感性認識上升到理性認識,概括出分數的意義,并在表達“部分——整體”意義的基礎上,進一步從測量、比和商等角度認識分數的含義。
認識幾分之一是認識幾分之幾的基礎,是整個單元的起始課。學生掌握了分數的基本知識,感悟數形結合的數學思想和方法,發展數感,為三年級下冊初步認識小數和五六年級進一步理解并掌握分數的意義、用乘除法解決分數問題打下良好的基礎。
從整數到分數是對數概念的一次擴展。對于學生而言,“分數”并不是全然陌生的概念,但與學生整日打交道的整數相比,二者無論在意義上還是讀寫方法及計算方法上都有很大差異。相對于整數而言,分數概念較為抽象而且有多種理解方式,并非是可以通過計數活動得到的一個數,而是代表了兩個量關系的相對量。學生要真正理解什么是分數,并不是一件簡單的事。
影響學習的唯一重要的因素,就是要探明學習者已經知道了什么,并應據此進行教學。所以,在設計這節課時,我一直在思考:以我班學生的學習基礎與學習能力,能否創設最簡單的情境,引導學生在直觀感受與動手操作中理解什么是分數。踏踏實實,步步為營,更多的感受和更新的體驗自然而然地滲透在每一個環節,這樣才能讓不同層次的學生都有所得,享受到數學帶給自己的成就感和快樂。
【教學過程】
一、微課導入,整體感知分數
師:同學們,這兩年來我們一直在和整數打交道,今天我們一起來認識一種新的數——分數(板書:認識幾分之一)。想必同學們在生活中已接觸過分數,關于分數,你知道些什么呢?請大家說一說。
生:我知道分數的寫法,上面有分子,下面有分母,就像媽媽背著孩子一樣。
生:分母和分子中間還有一條橫線,但我不知道叫什么。
生:分數有無數個,有的分數比1小,有的分數比1大。
……
師:分數在我國很早就有了,最初分數的表示法和現在可不一樣,請同學們一起來了解分數的發展歷史。(播放微視頻)
師:看了這段視頻,你對分數的了解是不是更多了?對照之前同學們的發言,說說你的收獲。
(學生各抒己見,逐步完善自己的認知結構。教師順勢教學分數的讀寫、各部分的名稱)
師:生活中常常能見到分數。你能找出下列句子中的分數嗎?請寫出來。
1.我們已經吃掉這個蛋糕的二分之一。()
2.美國約三分之一的成年人被認為是過度肥胖。()
3.上學期,我們班有四分之一的同學當上三好學生。()
4.這一期的黑板報中,“習作園地”占整個黑板報的八分之一。()
(集體反饋)
【設計意圖:來自學生的素材最是鮮活靈動,以開放的姿態引導學生參與知識的建構與生成,以更積極的態度從不同的角度接納與分析信息。而視頻中分數的發展史實際上也是人類社會文明的發展史,對學生的視覺與心靈都是一次沖擊,類似動漫的效果也備受學生的喜歡。之后的分數讀寫教學則是水到渠成。】
二、動手操作,初步探究分數
1.認識二分之一。
將學生作品展示到黑板上:

師:涂色部分的含義是什么?
生:我把這張紙看成一個蛋糕,平均分成兩份,涂色部分表示已經吃掉的。
師:你特別強調了“平均分”。如果不平均分呢?
師:你抓住了分數學習的最關鍵處,非常棒!那空白部分表示什么呢?
生:空白部分表示剩下的蛋糕。吃掉和剩下的各占一半,所以都用來表示。
師:真棒!可是為何大家畫的方法不一樣,卻都能表示出已經吃掉這個蛋糕的呢?
引導學生理解:不管分得的形狀是怎樣的,只要是把一個整體平均分成兩份,里面的每一份都是整體的。
師:是不是只有這三種分法呢?
生:我發現只要找到這個正方形的中點,過中點畫一條線,無論怎樣畫,都能將這個正方形平均分成兩份,每份都是這個整體的,所以有無數種分法。
2.創造幾分之一。
(教師指定全班三大組的學生用自己喜歡的方式分別表示余下三道題中的分數,并說說這個分數的含義)
(學生獨立思考后動手操作。教師巡視,指點需要幫助的學生)
(教師有選擇性地反饋學生作品,并請三名同學上臺解釋自己畫的圖是什么意思)
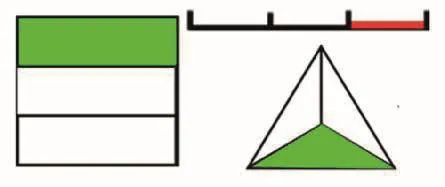
生:把所有美國成年人平均分成三份,有一份是過度肥胖,用分數表示。
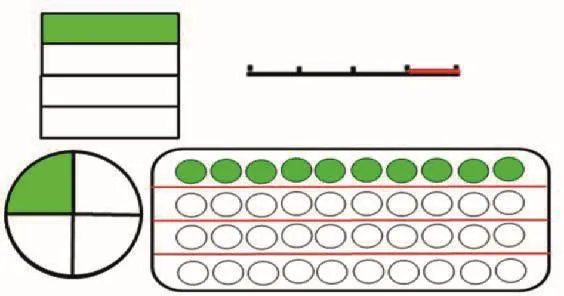
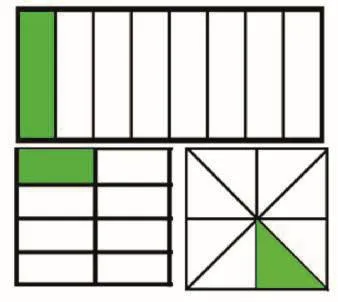
生:把整個黑板平均分成八份,有一份是“習作園地”,用分數表示。
(在解釋圖意的過程中,教師要注意及時糾正學生不規范的或錯誤的表達,強調“平均分”“分的是誰就是誰的幾分之幾”)
3.比較幾分之一。
(1)比較同分母分數的大小。
出示下圖:你從這幅圖中能看到哪些分數?

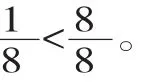
(2)比較同分子分數的大小。
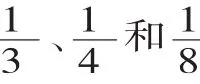

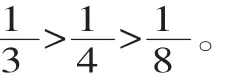
再出示一組線段圖和一組圓形,既是不完全歸納,又能驗證剛才學生的結論。
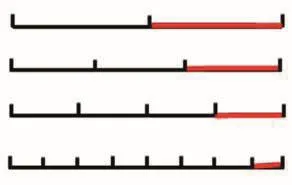
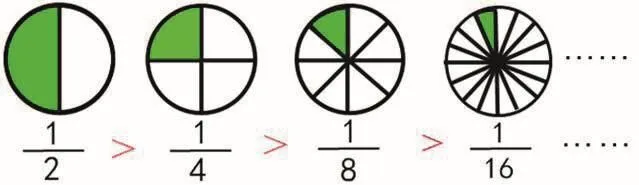
4.幾分之一變式練習。
下列說法對嗎?請你判斷并說說理由。

(1)上圖中的陰影部分不能表示“我們班有四分之一的同學當上三好學生”。()
有的同學一開始認為這兩道題都是正確的,理由是:第一題每份形狀不同,所以陰影部分不能表示出整體的四分之一。第二題的兩個二分之一肯定相等。教師不置可否,靜觀其變。
生:第一題不對,雖然每份形狀不同,但是確實是將整個圖形平均分成了四份,陰影部分表示其中的一份,所以能表示出整體的四分之一。
生:第二題中并沒有說兩個班的總人數一定相等,所以兩個二分之一也不一定相等。比如405班有40人,女生就有20人,406班有42人,女生就是21人,女生人數不相等。所以這道題也是錯的。
師:在什么情況下,這道題就肯定正確呢?
生:必須是兩個班的總人數相等的前提下,這道題才是正確的。
【策略分析:分數概念具有雙重性,既有“數的特征”,也有“形的特征”。只有從兩個方面認識分數,才能很好地理解并掌握它的本質意義。教師不僅要通過示范讓學生去感受幾何直觀的價值,更應該鼓勵學生積極利用各種圖形去直觀分析和解決問題。經歷獨立嘗試、交流共享、碰撞完善的過程,積累利用圖示學習數學的經驗,并用個性化的方式來記錄和表達自己的思維過程,學生的思辨能力與思維的縝密性就能得到較好的培養與發展。】
三、綜合應用,加深理解分數
1.完成練習二十第二題。
【設計意圖:從“用一張正方形紙(或線段、圓片等)表示出四分之一”到“根據一個整體的四分之一畫出整個圖形”,正向到逆向,一來一回,使“平均分”“分的是誰就是誰的幾分之幾”兩重意思的理解得到深化,幫助學生形成“帶得走”的能力。】
2.完成練習二十第八題。
【策略分析:各圖形不易直接看出平均分了幾份,且陰影部分分散出現,組合起來比較復雜,需要通過平移、旋轉、對稱等變換重新組合,這樣的練習可以培養學生靈活解決問題的能力,同時也滲透了分數的計算。】
3.七巧板是同學們熟悉的玩具,你從中發現了哪些分數呢?
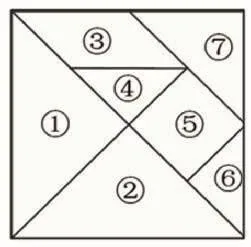
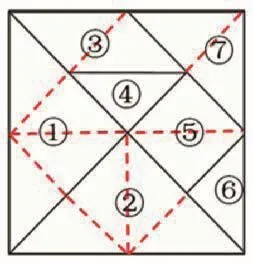
(1)()號圖形占整個正方形的();()號圖形占整個正方形的();
我還能繼續寫:()號圖形占整個正方形的()。
(2)我還發現:()號圖形相當于()號圖形的( )。
【策略分析:創設特定的學習情境,將七巧板與數學完美融合,引導學生打開思路,一句提示,一條輔助線,不需要更多言語,此時無聲勝有聲。】

