把握學習起點 聚焦思維難點
——“翻轉課堂”理念下《平行四邊形的面積》教學設計與思考

王麗兵

《平行四邊形的面積》是人教版五年級上冊《多邊形的面積》單元的學習內容之一。它是在學生初步認識了平行四邊形后，圍繞面積對平行四邊形的進一步研究，它也是后續學習三角形面積、梯形面積的知識基礎。教材以平行四邊形面積的公式推導為主要內容，以活動操作體驗為主要形式，注重新舊知識間的轉化與溝通。從這個角度來講，在整個小學數學“圖形與幾何”領域中，這一內容實質是起到了承前啟后的重要作用。

一、學生起點分析

一方面，在長方形和正方形面積的學習過程中，學生已經積累了通過數面積單位來描述圖形面積的經驗。與以往數面積單位不同的是，平行四邊形中首次出現不完整的“半格”，這對于學生無疑是一種挑戰，同時這也是轉化思想培養的有效載體。另一方面，由于長方形和正方形的面積計算，雖然有所區別，但從本質上來講都屬于“鄰邊×鄰邊”，這也就為較普遍的“平行四邊形的面積=鄰邊×鄰邊”的觀點找到了最合理的解釋。顯然，平行四邊形的面積無論是“鄰邊×鄰邊”，還是“底×高”，都已經成為本課教學的現實生態。

基于此，這些都為“平行四邊形的面積”的“翻轉”學習提供了諸多有利的條件和資源支持。因此，筆者從以生為本的角度出發，翻轉學習，改變學習方式，以求做一些突破。

二、教學過程設計

1.分享成果：感知圖形轉化意義。

師：同學們的學習任務單完成了嗎？那讓我們先在四人小組內交流一下自己的學習收獲和問題吧！不過，老師在這里對大家的交流提兩點小建議，你可以這樣來表達：

◇我設計的平行四邊形是這樣的……

◇我是用這樣的辦法數出平行四邊形的面積的……

【說明：通過課堂學習基礎現狀的討論，以相對民主和平等的方式討論明確本節課學習交流的方式。同時，規范學生的語言表達，提高學生學習交流的能力。】

師：老師課前也瀏覽了一些同學的預學作品，一起來看一下：

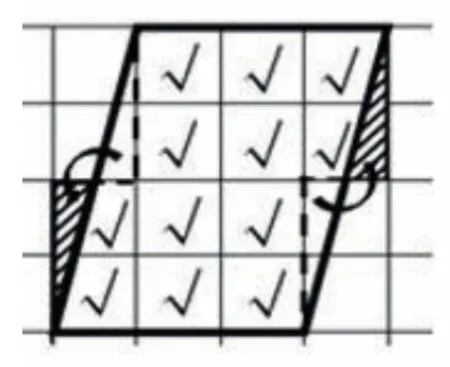
圖1　

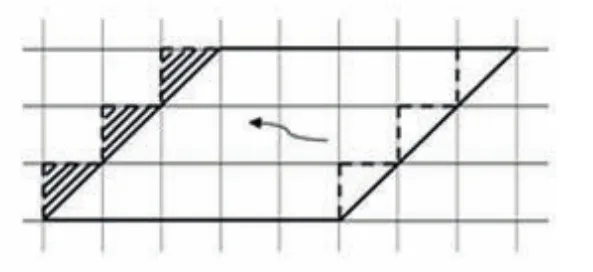
圖2　

圖3　

圖4　

師：大家看懂這四幅作品了嗎？能說說他們分別是怎樣數出了平行四邊形的面積嗎？

生：圖1通過旋轉的方式，將不滿整格的部分，拼成完整的圖形，這樣每層有3個正方形，一共有4層，所以是12平方厘米。或者，他給每個方格都打“√”，說明也可以一個一個數出來。

生：圖2是將右邊不滿格的部分平移到了左邊，使它們變成完整的一格。拼成以后每層有5個方格，一共有3層，所以面積是3×5=15平方厘米。

生：圖3通過平移以后得到了一個邊長是4厘米的正方形，所以，他是用“4×4”計算出平行四邊形的面積的。

生:圖4通過平移以后得到了一個長是4厘米、寬是1厘米的長方形，所以她是用“1×4”計算出平行四邊形的面積的。

【說明：通過對“學習單”中學生作品的選擇，筆者有意引導學生對高、矮、胖、瘦，不同形狀和方向的平行四邊形進行觀察和討論，使得學生明確“不滿整格”的部分是可以通過平移、旋轉進行拼組的，令原來的圖形面積單位更方便計數。】

師：現在請大家觀察一下這幾位同學在數平行四邊形面積的時候，有什么共同特點？

生：他們都把平行四邊形改變了一下，使不滿整格的全都拼成了整格的圖形。

生：它們有些還變成了我們以前學習過的長方形或正方形。

師：那么轉化以后的長方形和正方形，與原來的平行四邊形相比，什么變了？什么沒有變？

生：形狀變了，面積的大小沒有變。

教師小結：這種現象，我們在數學里稱之為“轉化”（板書）。

【說明：通過對四個不同形狀的平行四邊形的整體觀察，使得學生能夠體驗到平行四邊形“不滿整格”的部分都是需要轉化成長方形的，并且這個長方形與原來的平行四邊形的面積大小是一樣的。】

2.答疑解惑：突破知識理解難點。

師：分享了學習成果，我們來看一下同學們提出的問題：

（1）如果格子多了，該怎么辦呢？

（2）平行四邊形是不是只能切成三角形來拼？

（3）如果一個平行四邊形特別斜，那面積怎么數？

（4）將平行四邊形拉成一個長方形，可以用鄰邊相乘的方法計算嗎？

師：你能解決哪些問題呢？

生：第一個問題，如果方格特別多，我們可以把它們轉化拼成比較規整的圖形，然后計算即可。

生：第二個問題，我覺得也可以切成兩個梯形，它們也能夠拼成一個長方形。但剪的時候應該沿著高來剪才可以。

師：為什么呢？難道隨便切不行嗎？

生：隨便切就不能拼成比較規則的長方形或者正方形了。

生：第三個問題是擔心平行四邊形太斜，沿著高豎著切下來會切到圖形的外面，接下來就很難平移或者旋轉拼成完整的圖形了。

生：不能沿著高豎切，也可以沿著橫的高，橫切呀！只是這個長方形是斜的。

師：那對于第四個問題你怎么看？

師：暫時不能回答沒關系！那我們就重點來研究一下。現在請你選擇問題三或問題四其中一個研究，等會兒我們要進行反饋，來表達你自己的觀點。針對問題四，老師這里還有一個微視頻，你們研究完了想要驗證一下或者遇到問題了，可以上來點擊觀看。

【說明：以自主選擇的方式，針對學生困惑的問題展開研究討論，重點幫助學生加深對于“鄰邊相乘”和特殊平行四邊形面積計算問題的理解，以突破學生在思維理解上的難點。】

師：研究問題三的同學，對于這樣特別斜的平行四邊形，你們是怎么數它面積的呢？

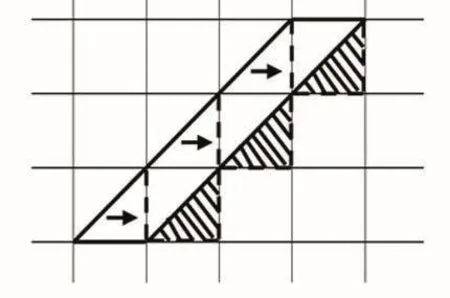
師：那對于問題四大家是怎么研究的？結論是什么？

生：將下圖中的深色三角形平移到左邊，將它的空缺補齊，上面斜線部分就是多出來的面積。

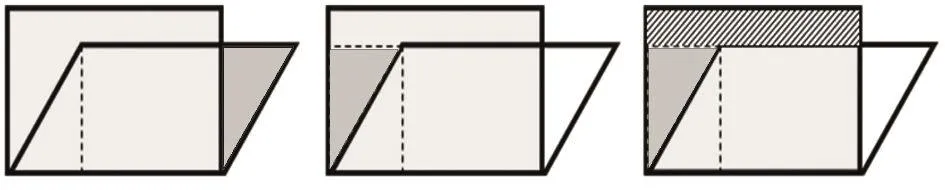
生：將平行四邊形拉成長方形和原來的平行四邊形面積不一樣。

生：這是因為原來平行四邊形的高變長了，所以面積變大了。

師：那將平行四邊形往下壓呢？

生：平行四邊形的面積會變小，因為它的高變短了。

師：對于用鄰邊相乘來計算平行四邊形的面積，大家怎么看？

生：這是不行的，因為面積變化了，所以不能代表原來平行四邊形的面積。

【說明：通過對“剪拼”和“拉動”兩種方法的對比研究，使得轉化思想在面積研究過程中的意義進一步凸顯。尤其是對拉動形成的長方形的觀察和比較，使得平行四邊形面積的變化變得愈加直觀和形象，更加凸顯“高的變化”對于圖形面積變化的作用，留給學生的印象更深刻。】

3.反思回顧：梳理知識學習方法。

師：回顧整節課，大家說說看，我們是怎么學習的？和以往有什么不同？

生：我們先看了微課視頻，做了一份課前學習單。然后在課堂上一起分享了我們的預學成果。之后還專門研究、討論、解決了同學們提出的一些問題。

師：那到底平行四邊形的面積應該怎么計算呢？你是怎么想到的？

生：平行四邊形的面積=底×高。

生：轉化后的長方形面積 =長×寬。

師：到底哪個對呢？

生：“長×寬”算得是轉化以后長方形的面積，“底×高”算得是平行四邊形的面積。

【說明：通過對學習過程的回顧，不僅有助于學生對于平行四邊形面積計算意義的理解，而且對于新的學習方式的提煉概括，也能有助于學生學習能力和素養的提升。】

三、教學實踐反思

1.以微課視頻為載體，前置知識學習。

學生對于平行四邊形并不陌生，但對其面積計算的認識和理解，大部分學生還只是停留在“只知其然，不知其所以然”的狀態。因此，筆者有意通過微課視頻內容的學習，避開一些和本課學習無關的非本質因素，直奔學習主題。不僅較為直觀地向學生介紹了平行四邊形面積的意義，并且通過“設計盡可能多形狀不同的平行四邊形，再清楚地表示出它的面積”為任務，驅動學生進行自主實踐和思考。一方面，可以幫助教師了解和掌握學生的知識起點和思維難點；另一方面，也為后續的操作和探究活動積累經驗并形成豐富的生態資源。

2.以任務驅動為形式，激化轉化需求。

如何激發學生認知的矛盾，激發學生圖形轉化的需要，從而實現學生思維認知的直觀外顯，這是本節課筆者力求能夠有所突破的又一思考。因此，筆者設計以“數”面積為學習任務，激發學生對于平行四邊形轉化的需求。其中，既包括一般形狀的平行四邊形，也包括特殊（特別斜）的平行四邊形。簡單來說，筆者有意幫助學生通過“數”平行四邊形面積，一方面“數”出規律經驗，積累方法意義的普遍性；另一方面要“數”出層次，激發認知沖突，感受方法意義的特殊性。顯然，從課堂生成的資源來看，學生為了更方便的“數”，生成了諸如割補、旋轉、平移等多種方法。不僅為本課學習提供了豐富的學習素材，同時也為平行四邊形和長方形的面積關系的討論埋下伏筆。

3.以問題疑惑為抓手，強化意義理解。

通過對學生學習問題的梳理和解答，重點圍繞“為什么不能用鄰邊相乘的方法來計算呢？”進行探討。應該說，“拉動轉化”突破了學生對于原有“割補轉化”認知的現狀，不僅能夠激發起思維認知沖突，而且也能引起學生對于等積轉化本質的關注。因此，筆者有意從學生的問題入手，結合平行四邊形模型框架的操作拉動，直接聚焦“鄰邊相乘”本質的意義，關注學生思維的難點。通過起初的操作觀察，再結合課中微課視頻的學習，使得學生逐步感受到“拉動”平行四邊形，雖然底邊和周長沒有發生變化，但由于高的長度的變化，使得平行四邊形面積也相應地發生了變化。不僅使學生對于平行四邊形面積計算的認知更全面和立體，也令本課思維的難點得到了關注和突破。