幾何直觀:提高學生思維能力的磨刀石
牛向華
借助幾何直觀可以把復雜的數學問題變得簡明、形象,有助于探索解決問題的思路,預測結果。幾何直觀可以幫助學生直觀地理解數學,在整個數學學習過程中發揮著重要作用。幾何直觀是學生直觀理解數學的手段,它是一種意識、手段,也是一種思維方式。在小學階段,幾何直觀主要通過數形結合的思想來體現。

一、“玩”中感知
在一年級的《重疊問題》中有這樣的情境:你看,穿花衣服的大雁多漂亮呀!從前面數,它排在第6;從后面數,它排在第3。這一行大雁一共有多少只呢?

為了幫助學生理解問題情境,展現學生的思維,可以讓學生通過演一演、擺一擺、畫一畫等活動初步感知幾何直觀。
1.演一演:舉手的同學為“花大雁”。

2.擺一擺:通過具體實物的擺一擺,學生初步感知用直觀的信息呈現數學問題。

3.畫一畫:有的學生用△代替花大雁,用○代替其他大雁。

通過演一演、擺一擺、畫一畫,學生很容易看出,花大雁被數了兩次,即重疊了一次,因此可以這樣列式解決重疊問題5+3=8(只)或 6+3-1=8(只)。
通過畫一畫,把具體事物抽象成幾何圖形,擺脫了實物的束縛,讓學生體會畫圖的形象性、簡潔性和簡便性,并用“形”刻畫和解釋了問題,做到了數形結合,使幾何直觀在學生心中開始萌芽,學生聞到了幾何直觀的氣味。
二、“思”中成長
如:在《簡單的搭配問題》中,學生經歷了幾何直觀輔助自己有序思考的全過程,體會到了幾何直觀的必要性。
師:2件上衣和3條裙子一共有多少種搭配方法呢?你能通過擺一擺找到答案嗎?
生:
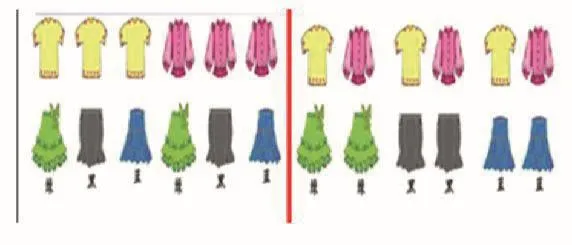
師:每次用學具擺很麻煩,怎么辦?
生:連一連。
師:實物太麻煩了,能不能想個辦法再簡單些!
生:可以用符號或圖形代替!

學生在一步步的方法優化中,經歷了有序思考和符號化的過程,此間幾何直觀起到了非常重要的作用。學生通過擺一擺的實物直觀理順了2配3的順序,然后再去體會這種順序還可以用更簡單的方式表達出來,做到數形的完美結合,幾何直觀在學生心中逐漸成長。
三、“用”中提升
在《植樹問題》一課中,學生在用幾何直觀輔助理解題意的過程中,數學思想方法也悄然入心。
師:20米的小路,每5米栽一棵樹,一共可以栽多少棵樹?你能自己畫圖試試嗎?
生:
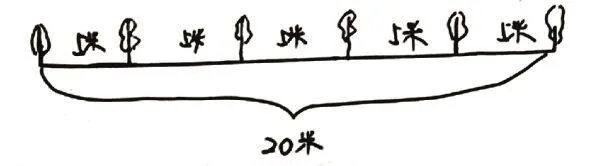
師:生活中還有沒有像這樣的植樹問題呢?
生:站隊的時候有植樹問題。
生:插彩旗的時候有植樹問題。……
師:我們來看看剛才大家提到的這些問題是不是植樹問題呢?

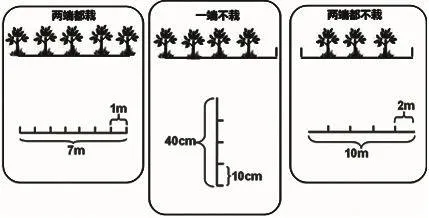
生:它們都是植樹問題,有“樹”也有“間隔”。
學生們通過幾何直觀把實物圖抽象成線段圖,較好地體會了一一對應思想。并且很清楚地感受到“樹”與“間隔”,還能迅速地將它們歸為一類問題,很好地體會了模型思想。在用幾何直觀解決問題的過程中,學生的思維得到了訓練,數學素養得到了提升。
四、“練”中自覺
在有了初步感知、親歷體驗、素養提升的基礎上,學生還要在平時的數學學習中自覺去應用,讓幾何直觀成為一種思維習慣,以便更好地幫助自己分析問題、解決問題。
例如文中一開始提到的案例,如果學生有用幾何直觀解決問題的習慣,哪怕在頭腦中想象出線段圖的樣子或記住植樹問題這種數學模型中段數與次數的關系,都會輕松準確地解決問題。
再如,在一次練習中有這樣一道題:倉庫里有一批貨物,第一次運走這批貨物的,第二次運走9噸,此時運走的貨物與剩下的貨物噸數的比是7:5。這批貨物一共有多少噸?正在很多學生束手無策找不到解題思路時,已經有部分同學做出來了。我讓其中一名學生板演時,他就用到了畫線段圖這種幾何直觀思想分析數量關系的方法,輕而易舉地解決了問題

當然,學生有能力水平和思維風格的差異,面對相同的問題,會出現不同的方法,表現出不同的思維特點,我們也不必強求所有學生用幾何直觀的方法來表征問題、探索思路。在日常的練習中,幾何直觀作為一種實踐經驗,還要逐步內化為思維經驗,從而成為一種思維自覺。
幾何直觀能力的培養需要我們教師在讀懂教材、了解編者意圖的基礎上,在教學中長期關注,并有意識地滲透。首先我們要選好“點”,即幾何直觀在哪里用。幾何直觀作為一種手段或工具,我們要明確它用在什么地方最恰當。我們要有效預設教學,選好幾何直觀能力培養的點,這樣會起到事半功倍的效果。其次我們更要把握好“度”,即用到什么程度停止。數學的本質是抽象與推理,所以直觀不是我們的目的,借助幾何直觀實現抽象的思維發展才是我們的最終目的。幾何直觀完成自己的任務就要迅速抽身讓位于抽象或者推理,否則將會限制學生的思維發展。我們還要讓學生感受幾何直觀在數學學習中的作用,感受它的優勢,逐漸將幾何直觀轉化為數學學習的內在需要。
總之,幾何直觀能力的培養是一個持續的過程,如果我們從一年級開始就堅持并適當地滲透、引導,在數學思考過程中,學生的頭腦中就會逐步有一個看不見的“形”的支撐,逐漸形成幾何直觀的意識、能力和思維方式,從而提升學生的數學素養。

