知其然并“探”其所以然
——《四邊形內角和》教學與評析

執教/付 密 評析/劉 莉（特級教師）

【課堂寫真】

一、故事導入——激發探究興趣

師：三角形的內角和是多少度？上節課，我們用了什么方法研究？

視頻展示：四邊形兄弟今天有場擂臺賽：

師：它們在爭論什么？（內角和）

板書課題：四邊形的內角和。

二、體驗過程——探其所以然

1.猜想四邊形的內角和。

師：你猜四邊形的內角和是多少度？

師：為什么是360°？

生：長方形、正方形比較特殊，它們的4個內角都是直角，內角和是360°（學生邊說，課件邊展示）。

師：其他四邊形的內角和也會是360°嗎？你準備用什么方法驗證？

2.驗證或研究任意四邊形的內角和。

（1）驗證方法。

（同桌商量驗證方法，學生匯報）

生：量一量、拼一拼、分一分。

（2）驗證過程。

師：手指尖上出智慧，打開學具袋，小組合作，動手研究吧！

（教師巡視，發現問題，針對性地進行指導研究有困難的學生）

（3）匯報交流。

①量角求和。

學生匯報四邊形內角和度數 361°、360°、358°……

師：你發現了什么？

生：這些數據要么等于360°，要么接近360°。

師：為什么量沒能得到統一的答案？還有什么方法驗證？

②拼角求和。

學生邊演示邊說明。把4個內角剪下來，拼成一個周角，周角是360°，四邊形的內角和是360°。

③分角求和。

師：“四邊形”菜地能隨便撕嗎?還有什么方法驗證?

生1：分一分。連接一條對角線，把四邊形分成兩個三角形。

生2：一個三角形的內角和是180°，兩個三角形的內角和是360°，四邊形內角和是360°。

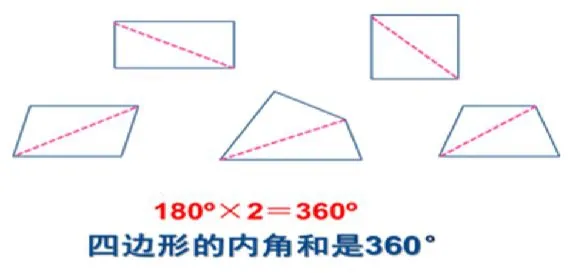
師：四邊形有4個內角，兩個三角形有6個內角，它們的內角和相等嗎？為什么?

生：四邊形的1個內角分成了三角形的2個內角，四邊形的2個內角分成了兩個三角形的4個內角，內角和都是360°。

（課件演示）

師：所有四邊形內角和都是360°嗎?

生：是的，它們都能分成兩個三角形。

師：將四邊形分成兩個三角形，四邊形內角和轉化成三角形內角和的問題。轉化是數學中常用的方法。

3.得出結論：四邊形內角和是360°。

師：我們通過3種不同的驗證方法，得到同一個結論：四邊形內角和是360°。哪種方法最簡便、最直接？

生：分一分。“量”容易產生誤差；“拼”的應用有限制，考試卷、菜地就不能撕；只有“分”最簡便。

三、課堂延伸——推廣探究結論的應用

1.基本練習。

出示自制教具四邊形。

師：無論怎么拉，雖然形狀變了，但內角和都是360°。拉到極限時，兩個內角拉成180°，另外兩個角拉成0°，內角和是180°+180°+0°+0°=360°。

【設計意圖：用推理驗證了四邊形內角和是360°，同時潛移默化地滲透了極限思想。】

2.升華練習。

將一個四邊形分成兩個四邊形，每個四邊形的內角和是多少度？兩個四邊形合成一個四邊形，它的內角和是多少度？

3.類推練習。

學生獨立完成計算五邊形內角和。

4.舉一反三。

師：你準備怎樣研究六邊形、七邊形、八邊形……的內角和呢？

生：把多邊形分成三角形，看分成三角形的個數就能求出多邊形的內角和。

師：千金難買回頭看，回到起點看三角形！

三角形個數=邊數-2；多邊形內角和 =360°×三角形個數；多邊形內角和=360°×(邊數 -2)。

推導出多邊形的內角和后，練習計算十邊形、十二邊形、一百邊形的內角和。

5.拓展練習。

園林工人要重新規劃草坪，如果將假山處的內角去掉，剩下多邊形的內角和是大了？還是小了？

【課后評析】

《四邊形內角和》是2011版教材新增的內容，是基于學生已經知道三角形內角和及四邊形基本特征基礎上的一次探索規律活動。讓學生了解四邊形的內角和是360°是《數學課程標準》規定的教學內容和教學要求，這里講的“了解”不是接受和知道，而是發現并簡單應用。學生根據已有經驗猜想四邊形內角和是360°。為什么是 360°？學生只知其然但不知其所以然，所以，本節課的重點就是要讓他們主動地去“探其所以然”——引導學生通過觀察、操作、類比、歸納等一系列活動，經歷從特殊到一般的探究學習過程，進而研究得出四邊形的內角和，嘗試解決有關多邊形內角和的問題。

著名數學家陳省身先生指出：“數學是自己思考的產物，用自己思考的見解和別人的見解交換，會有很好的效果。”本節課，教師提供給學生一種自我探索、自我思考、自我創造、自我表現和自我實現的機會，使學生最大限度地投入到觀察、思考、操作、探究的活動中。在探究是不是所有的四邊形的內角和都是360°時，給學生提供一些材料，為學生留有足夠的時間和空間，讓學生通過小組合作交流，主動探索驗證四邊形內角和的“猜想”。同學之間通過合作交流、智慧碰撞、思維火花閃現，出現了量一量、拼一拼、分一分推理等多種驗證方法，從而得出四邊形內角和是360°的重要性質。“是否任何四邊形的內角和都是360°呢？”教師趁勢再次引導學生同桌合作，動手驗證。這樣教學，學生不僅經歷并感悟了猜想——驗證——得出結論——應用的科學研究的過程，而且積累了數學活動經驗。更為重要的是，通過這些過程使學生明白：探究問題有不同的方法、途徑，并且方法之間可以互為驗證，達到結論的統一，從而使學生明白獲得探究問題的方法比獲得結論更為重要。

我們可以利用方法的“慣性”思考，實現課堂上以盡量小的教學成本取得最大教學效益的目標。當學生已經用量、拼、分三種方法求得四邊形內角和，并發現“分”這種方法更科學、方便，也初步體會了四邊形內角和與三角形個數之間的關系時，教師提出問題：要求六邊形、七邊形、八邊形……的內角和其實就是要看什么呢？引導學生在探索四邊形內角和的基礎上利用合情推理和轉化的數學思想推導出多邊形內角和公式。這樣教學，直接將探究四邊形內角和的方法類比遷移到其他多邊形內角和的研究中，求多邊形內角和的問題直接轉化為求若干個三角形內角和的問題，學生不用再另起爐灶花費時間思考。

在探究多邊形內角和時，表格更容易幫助學生理清題目數量關系，探索規律，總結方法。本節課中，教師通過強化表格的作用，讓學生體會到用表格解決問題的奇妙。