《分數四則混合運算》教學設計
程 香
【教學內容】
蘇教版六年級上冊第五單元例1、練一練。
【教學目標】
1.能結合具體的實例,主動把整數、小數四則混合運算的運算順序推廣到分數四則混合運算中來,并能正確地進行計算。
2.知道整數的運算律對分數運算也同樣適用,能應用運算律進行有關分數運算的簡便計算。
3.在運用已有知識和經驗進行分數四則混合運算和解決實際問題的過程中,進一步豐富對四則混合運算的認識,提高運算能力;積累解決問題的經驗,增強應用意識。
【教學過程】
一、四則運算意義回顧
課件逐題出示問題:
1.小明養了20條金魚,小紅養了12條金魚,兩人一共養了多少條金魚?
2.東東家買來一袋10千克的面粉,吃了4.5千克,還剩多少千克?
學生自由讀題后在隨堂本上列式。
指名說算式,教師板書,學生說明列式理由。
師:“+-×÷”這四種運算可是咱們的老朋友了,你能談談對它們的認識嗎?(什么情況下用加法?什么情況下用減法?什么情況下用乘法?什么情況下用除法?)
學生計算,指名說得數。
小結:因為解決問題的需要,就產生了加減乘除這四種運算,這四種運算就統稱為“四則運算”。板書:加減乘除 四則運算
【設計意圖:借助一步計算實際問題,分別復習“加減乘除”這四種運算的含義與計算方法,讓學生認識到雖然參與運算的數是在不斷發展的,但是算理并沒有改變。】
二、分數四則混合運算順序溝通
師:整數、小數、分數,參與運算的數在不斷發展,問題也會逐漸復雜起來,僅憑一步計算不能解決了。
課件出示:
指名列式,并說明列式理由,教師板書算式及計算過程。
師:有時候兩步計算也不能解決了。
課件出示:
指名列式,并說明列式理由,教師板書算式及計算過程。
師:在一道算式中,含有兩種或兩種以上的運算,就稱為四則混合運算。今天我們就來研究分數參與的四則混合運算。
師:你覺得分數四則混合運算的順序是怎樣的呢?
【設計意圖:由一步計算到兩步計算再到三步計算,幫助學生認識到計算是基于解決實際問題的需要而產生的。因為問題越來越復雜,參與運算的數也越來越多元,分數四則混合運算學習的必要性就得以凸顯,運算順序自然得以溝通。】
三、運算律的推廣
1.出示例題:

學生獨立列綜合算式解決,指名上黑板完成。
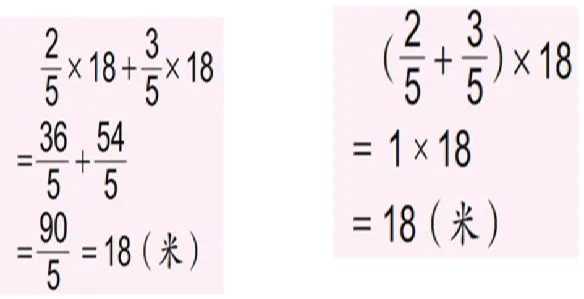
全班交流:學生說說每一步求的是什么?算式之間有什么聯系?
教師小結:整數的運算律對于分數同樣適用。
2.我們曾經研究過哪些運算定律或者運算性質呢?課件出示

3.學生完成“練一練”第2題:計算下面各題,注意使計算簡便。
指名上黑板完成后集體交流。
【設計意圖:通過例題兩種方法的對比,學生感知曾經學習的運算律也可以使分數四則混合運算變得簡便,進而復習曾經學習的運算律,為分數四則混合運算的簡便計算做好準備。】
四、鞏固提升
1.課件出示“練一練”第1題。

學生獨立完成,指名上黑板完成。
2.完成“思考題”。

【設計意圖:及時的鞏固練習,并且在集體交流中糾錯,提高學生靈活運用運算律計算的能力。】
五、全課總結
師:通過這一節課的學習,你有哪些收獲?在計算分數四則混合運算時,你想給你的小伙伴一些提醒嗎?
【教后反思】
計算課很重要,“+-×÷”貫穿了整個小學階段的數學教學,譬如本課,就是學生在小學階段分數運算學習的最后任務,是學生計算技能和能力的重要組成部分,也是進一步學習有理數、分式等運算的重要基礎。而在本課之前,學生已經掌握了整數、小數四則運算及四則混合運算的運算順序及運算律,并能運用運算律進行有關的簡便計算。
計算課的內容編排很簡單,每冊教材中的計算教學基本都會通過問題情境引出計算的需要,在算法的探究中理解計算的道理,在練習中鞏固計算方法,提升計算技能。本課也不例外,教材先通過解決生活中常見的實際問題,引入分數四則混合運算,然后學生嘗試計算,在嘗試中舊知主動遷移。
六年的時間,學生已經有了充分的計算學習的經驗,也正因為如此,常規的計算教學很難激發出學生的學習熱情,碎片化的計算經驗即使遷移過來也不能完整建構。基于這些考慮,本課教學基于教材編排而又突破教材局限,以學生的認知結構發展與計算知識的發展變化為教學的兩條主線展開。
從知識的發展變化來看,本課由四道一步計算問題引入,分別復習加、減、乘、除四種運算的含義與計算方法,讓學生認識到雖然參與運算的數是在不斷發展的,但是算理并沒有改變,自然把學生的認知重點引到四則運算的含義上。
問題逐漸復雜,兩步計算再到三步計算,幫助學生認識到計算是基于解決實際問題的需要而產生的。“把1升果汁倒滿3小瓶,每小瓶升,剩下的平均倒在2個杯子里,每個杯子里倒進果汁多少升?”在解決這個問題時,出現了不同的聲音:由1-,到,再到,交流的過程也就是在不斷完善建構的過程。就是在這樣的交流中,教師及時指出這就是“四則混合運算”,今天學習分數四則混合運算。學生自然而然地經歷由四則運算→四則混合運算→分數四則混合運算的知識發展過程中,感受知識的內在聯系和結構。
從學生認知結構發展來說,隨著知識的復雜,所需要的認知操作也會變得復雜,在由一步到兩步運算的時候,顯然一步運算的認知結構解決不了當前的兩步運算問題。學生通過順應,認知結構由原先一步擴充到兩步,當遇到三步運算時,再由兩步擴充到三步,認知結構也不斷地擴充。我們的學生,就是在不斷面對復雜的知識任務過程中,不斷地擴充自己的認知結構,使得學生的認知不斷上升發展。當然學生的學習并不只是通過順應的方式,同化的方式也時常發生,如果學生整數四則混合運算學得很好,就會自然地將過去所學的整數四則混合運算遷移到分數四則混合運算,將分數四則混合運算同化到學生四則混合運算的認知結構下。
無論是從知識還是學生認知角度出發,我們都看到了生長的力量,只有平時培育寬松的課堂土壤,這種自然的生長才會不自覺地迸發。

