無痕教育策略的有效實施
——徐斌老師《倍的認識》一課教學感悟
朱 紅
徐斌老師倡導的是“教育的無痕境界”,即把教育的意圖和目的隱蔽起來,通過間接的其他方式,讓學生在不知不覺中被教育、學到新的知識和學習數學的有效方法,讓學生運用數學方法去研究更新的知識。下面以徐斌老師《倍的認識》一課教學為例,談談筆者對無痕教育策略如何有效實施的幾點感悟與思考。
一、在不知不覺中引入新知
要想讓學生在不知不覺中開始學習新知,教師就必須先熟悉教材,并把握好前期的知識結構和要學習的知識之間的聯系,才能為學生選準合適的認知起點,讓學生在不知不覺中開始學習新的知識。
【片斷一】新知引入
師:老師先考考大家原來學過的知識,有信心回答好嗎?
生:有!
師:6里面有幾個3?
生:6里面有2個3。
師:10里面有幾個2?
生:10里面有5個2。
師:15里面有幾個5?
生:15里面有3個5。
師:怎樣列式計算出來?
生:15÷3=5。
師:也就是求一個數里面有幾個另一個數用什么方法計算?
生:除法。
在上述教學片斷中,徐老師在課前給學生們復習了“一個數的里面有幾個幾用除法計算”的舊知,它和“倍的認識”新知識內容有著緊密的聯系,為后面解決一個數是另一個數的幾倍作鋪墊,也為隨后“倍的認識”的教具板演奠定基礎。讓學生在不知不覺中進入新知的學習,教學的效果會很好。如我在教學《認識眾數》時,創設了學生感興趣的教學情境——點擊名人圖片來引入“眾數”:用翻轉名人圖片的動畫來調動學生的學習興趣,完成學生的猜想;通過點擊名人圖片,引導學生復習數對知識;在學生統計圖片數量時,強調劉翔圖片出現的次數最多,讓學生明白“眾數”是尋找出現次數最多的圖片,而不是這張圖片出現的次數,從而在認識眾數和找眾數時不會出現判斷失誤。這樣導入,達到三個方面的教學效果:激發學生的興趣;復習以前的知識;讓學生初步感受眾數的本質——出現次數最多。實踐證明,要讓學生在不知不覺中進入新知,教師自己要研讀教材,真正掌握教材。
二、在潛移默化中理解新知
讓學生在潛移默化中理解新知,教師需要站在學生的角度問問自己:這樣設計能讓學生更好地理解嗎?此外,還要從學生的學習興趣出發,借助形象直觀的教學手段,順應學生的學習心理,由簡到繁,搭起新舊知識的橋梁。
【片斷二】新知學習
首先出示情境圖:學校花壇里有藍花2朵,黃花6朵,紅花8朵。讓學生提出數學問題:1.一共有多少朵?2.紅花比藍花多幾朵?再介紹還有一種“比”的方法叫“倍”。
接著在黑板上擺出藍花教具,在下面畫出黃花的朵數,兩個兩個的畫,兩個圈在一起介紹“倍”的含義。
然后帶領學生在教材上圈一圈,填一填。進一步提問:紅花有8朵,8里面有幾個2?用什么方法計算?
最后進行變式訓練,1.如果藍花2朵,紅花有10朵,紅花是藍花的幾倍?怎樣用除法計算?2.如果藍花2朵,紅花有4朵,紅花是藍花的幾倍?怎樣計算?3.黃花6朵,現在藍花增加1朵成3朵,如果依舊要讓黃花的朵數是藍花的3倍,可以怎么辦?4.如果藍花變成4朵,依舊要使黃花的朵數是藍花的3倍,可以怎么辦?
徐老師在教授新知的教學過程中,非常重視從學生的思維出發,用學具、畫圖這樣簡單直接的教學方法將新知逐漸滲透,由簡入繁,讓學生逐漸理解新知。新課開始,徐老師請學生自己提問題,在介紹新的知識“倍”時,運用了新舊知識的對比,讓學生知道還有一種“比”的方法叫“倍”;學生觀察教師的教具,自己板演畫出黃花的朵數,這是學生初步感知“倍”的開始,沒有正確的感知就不可能認識倍的本質。心理學研究表明:學生感知越豐富,建立的表象越清晰,就越能發現事物的規律,獲得知識。徐老師在教學中給學生提供了充足的能揭示“倍”的感性材料,并能一步步引導學生動手做、動腦想、動口說、動眼看,使學生在圈一圈、填一填、說一說中獲得豐富的感性認識,建立清晰的“倍”的表象,搭建起知識結構物化與內化的橋梁,促使學生形成了初步的“倍”的認識;在學生大量感知“倍”的問題后,徐老師又給予學生充足的時間和空間,讓學生根據自己的感知,用自己的思維方式自由地觀察思考簡單的“倍”的問題、再用增加藍花的朵數加深學生對“倍”的問題的認識,逐步從感性認識上升到理性認識——計算。這樣增強學生主動探索和獲取數學知識的能力,促進學生創新能力的發展。
“天下難事,必作于易”,讓學生從簡單的兩種花的朵數來研究倍的問題,課件出示“黃花6朵,現在藍花增加1朵成3朵,如果依舊要讓黃花的朵數是藍花的3倍,可以怎么辦?”徐老師的教學方法滲透的自然、有效。我認為“舉例”和“由簡到繁”的教學方法在我們數學的課堂上是運用最廣泛的,不僅在課堂上運用,平時小學數學的考試中也有許多題目能用到這兩種方法,而且這兩種方法往往是相輔相成的,聯合起來運用效果會更好。如課堂中,我在教授乘法分配律的時候,課始先問:“同學們還記得加法交換律嗎?”讓學生通過舉例的方法復習加法交換律,再推出新的課題——乘法交換律。授新課中,讓學生根據例題列式子:4×25=100(人)25×4=100(人)2×25=50(人)25×2=50(人)5×25=125(棵)25×5=125(棵)通過觀察發現:交換因數的位置,積不變規律。再讓學生任意舉例驗證猜想和發現,學生通過舉例充分體會了交換律的規律。
三、在循序漸進中掌握新知
課堂中的練習對學生掌握新知起到鞏固的作用,精心設計、組織好課堂上的練習不僅會使學生對新知的理解更深刻,而且會對數學課堂充滿學習興趣。
【片斷三】鞏固練習
1.拍手游戲。
一個學生拍任意次數手,讓另一位學生拍他拍手次數的倍數。如拍3下,要拍3倍,另一個學生就拍9下,并且是3下3下的拍。
2.操作小棒。
要使下面的小棒數是上面的小棒數的5倍,如何增加或減少小棒的數量。
(1)第一行擺3根小棒,第二行怎么擺是第一行的5倍?
(2)第一行擺4根小棒,第二行擺28根小棒,怎么滿足題目的要求?
3.觀察圖形。
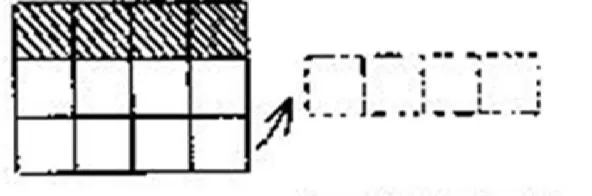
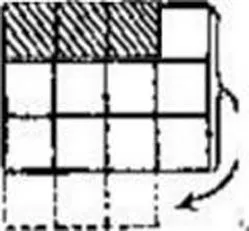
(2)提問:紅方格有幾個?藍方格有幾個?藍方格的個數是紅方格的幾倍?(可移動右邊三個藍方格)
4.測量線段。
要使第二條線段的長度是第一條線段長度的4倍,如何畫?(出示一段2厘米的線段)
從上述鞏固練習的教學片斷可以看出,徐老師的鞏固練習不僅形式多樣,還能充分調動學生的學習積極性,真正起到了鞏固的作用。我在教授《鴿巢問題》時,練習中就運用了游戲練習,如讓學生抽撲克牌,至少抽幾次能抽到同一花色?學生回答后,師生一起用游戲驗證規律、總結規律。實踐證明,學生非常喜歡這種鞏固練習的方法,而且知識點也掌握的很牢固。

