城市軌道交通列車運行圖魯棒性優化模型

曹志超, 袁振洲 , 李得偉, 張思林, 馬伶伶

(1.北京交通大學 城市交通復雜系統理論與技術教育部重點實驗室，北京　100044；2.北京交通大學 軌道交通控制與安全國家重點實驗室，北京　100044；3.中國民航大學 民航空管研究院，天津　300300)

隨著城市軌道交通技術裝備水平的提高，以及為滿足乘客出行要求，客流高峰時段高密度行車已成為城市軌道交通運輸的重要特征。例如，北京市城市軌道交通在移動信號閉塞系統[1]下已實現90 s的列車發車間隔。但是，在高密度行車條件下列車一旦晚點，對整個路網的運輸組織會產生很大的影響。因此，如何在計劃階段通過調整列車運行圖以減小此影響，從而實現城市軌道交通列車運行圖抗干擾性(即魯棒性)的優化，是高密度行車條件下列車運行計劃編制和調整的重要目標。

傳統的列車運行圖優化模型較少考慮為滿足客流需求而導致的隨機干擾，缺乏魯棒性優化的空間。國內學者對計劃階段運營管理的研究重點多集中在列車開行方案上，對城市軌道交通列車運行圖研究較少。文獻[2]提出以平峰時段換乘客流總等待時間最少為目標的網絡周期運行圖編制方法；文獻[3]提出以列車總旅行時間最少和使用動車組車底數最少為目標的高速鐵路周期性運行圖優化模型；文獻[4]研究了城市軌道交通車底運用方式、列車發車間隔和首末班車銜接方案等共線交路列車運行圖鋪畫的關鍵問題；文獻[5]提出以鐵路企業效益最大化為目標的旅客列車開行方案和運行圖綜合優化的雙層規劃模型；文獻[6]提出2種不同恢復方法的列車運行圖可恢復魯棒性的優化模型；文獻[7]提出采用“時間控制點法(Time-control strategy)”提高公交開行計劃魯棒性的優化模型。以上研究為準確理解列車運行圖編制問題提供了重要的研究基礎。完成城市軌道交通列車運行圖的編制需要以下3個基本步驟。

(1)確定列車的發車頻率或發車間隔；

(2)規定列車的開行區段、折返交路和停站方案；

(3)確定列車的出發時刻、到達時刻、緩沖時間(Buffer-time)、區間運行時間。

基于以上背景，本文以步驟(3)為研究目標，考慮乘客在車站的等待行為和列車的交互關系，以城市軌道交通列車運行圖擾動時間之和最小化為目標，構建滿足客流需求的城市軌道交通列車運行圖魯棒性優化模型，并提出求解算法。

1　問題描述

城市軌道交通列車運行圖之所以受到干擾，不能按計劃時間開車，除設備技術故障外，很大程度上是由于客流高峰時段內乘客持續上車，使列車車門無法關閉而導致列車出發時刻延誤，進而產生列車晚點。如果列車運行圖的魯棒性差，還將導致列車晚點傳播范圍增大，甚至有些列車停運。

本文的研究思路為：在計劃層的列車運行時段內，調整列車緩沖時間，以優化列車運行圖的魯棒性。其中如何確定站間的緩沖時間是優化列車運行圖魯棒性的關鍵。因為如果緩沖時間過長，勢必會延長乘客在途時間，降低列車發車頻率；但緩沖時間過短，又無法提高列車運行圖的抗干擾能力。

本文首先詳述列車運行組織計劃的約束，然后在考慮列車載客能力的情況下，基于歷史客流數據并通過候車乘客與列車的交互關系確定列車的實際停站時間，最后基于列車運行圖擾動時間的遞推關系進行建模。

為方便建模，對列車的運行特征作如下假設。

(1)基于文獻[8]的假設，以城市軌道交通單一線路為研究對象，并采用站站停的停站方案。

(2)根據國內外城市軌道交通運營實踐，采用2站式的長交路運行，即始發站1為車輛段所在站，終到站n為列車折返站。

(3)所有列車編組一致，即列車具有相同的載客能力(列車內的座位數與可容納站立人數之和)，并用C表示，人·列-1。

(4)每個車站同時僅能容納1列列車，全線不允許有列車越行。

(5)列車站間運行包括3個階段：起動加速階段、勻速運行階段和制動減速階段。

2　模型構建

令城市軌道交通線路網絡N=(J,E)，其中J={1,2,…,j-1,j,…,n}為車站集；E={e(j-1,j)|j∈J}為區間集，區間e(j-1,j)∈E為車站j-1與相鄰車站j之間的區間；區間e(j-1,j)的里程長度(簡稱站間距)記為l(j-1,j)，m。

2.1　列車運行組織計劃約束

設在運營時段[t0,te]內計劃開行的列車的集合為I={1,2,…,i-1,i,…,m}。

在E上的列車計劃出發時刻需滿足安全追蹤間隔時間的約束，即

(1)

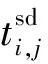
根據假設(4)和(5)，列車運行圖中任意一班列車的計劃到達和出發時刻存在如下關系。

(2)

(3)

(4)

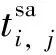
由于有

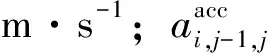
因此將上述公式帶入式(4)后可得

(5)

列車勻速運行速度vi,j-1,j應滿足

(6)

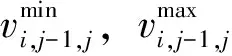
(7)

2.2　乘客和列車的交互關系約束

在車站j等待乘坐列車i的客流量Wi,j為

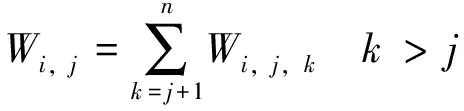
(8)

其中，

(9)

式中：Wi,j,k為在車站j等待乘坐列車i前往車站k∈J的客流量，人；Li-1,j,k為因上一班列車i-1滿員而滯留在車站j的打算前往車站k的客流量，人；λj,k為從車站j出發前往車站k的客流到達率，人·s-1。

列車i在車站j的下車客流量Ui,j為

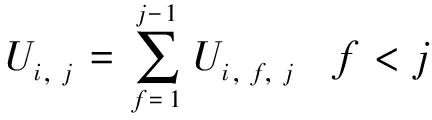
(10)

其中，

Ui,f,j=Wi,f,j-Li,f,j

(11)

式中：Ui,f,j為列車i上在車站f上車且在車站j下車的客流量，人。

列車i在離開車站j時，車內客流量Qi,j為

Qi,j=Qi,j-1-Ui,j+Bi,j

(12)

其中，

(13)

(14)

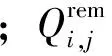
在客流高峰時段，由于受列車載客能力的限制，列車i在車站j滯留的客流量Li,j為

(15)

Li,j還可以由下式得到，即

(16)

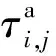
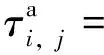
(17)

式中：β1，β2，β3，β4分別為擬合參數；d為每列車上下乘客的車門數量，個·列-1。

2.3　列車運行圖魯棒性約束

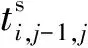
(18)

其中，

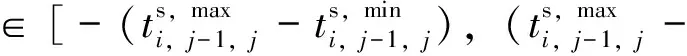
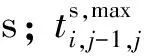
(19)

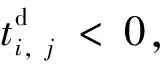
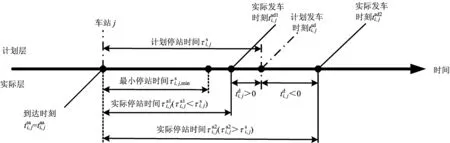
圖1　列車運行圖擾動時間

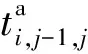
(20)

式中：δi,j-1,j為列車i在區間e(j-1,j)的可恢復因子，0≤δi,j-1,j≤1，令δi,1,2=0，即列車i在始發站正點出發。

(21)

類似式(2)和式(3)，列車i在車站j的實際出發時刻為

(22)

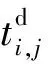
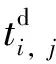
(23)

基于式(18)，上式可進一步寫成

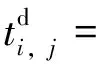
(24)

因為列車在始發站正點發車，那么

(25)

如果令

因為t和τ可根據歷史客流量數據計算得到，δ為經驗取值變量，所以將t，τ，δ作為輸入變量，而緩沖時間x則為輸出結果。

2.4　優化模型

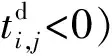
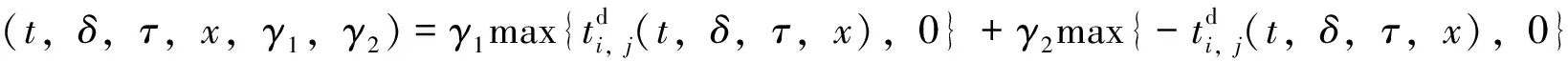
(26)

γ1和γ2可通過列車實際運行數據進行標定。

以式(1)—式(26)為約束條件，列車運行圖的擾動時間之和最小化為目標，構建的城市軌道交通列車運行圖魯棒性優化模型為

(27)

3　求解算法

優化模型為單目標非線性混合整數規劃模型，主要通過調整緩沖時間實現列車運行圖擾動時間之和最小，從而使列車的計劃出發時刻與實際出發時刻盡可能一致。由于模型中需要輸入的變量較多，直接求解具有很大難度，因此本文采用改進的遺傳算法和計算機模擬的方法進行求解，其總體思路是首先將復雜的非線性規劃問題通過遞推公式轉化為線性規劃問題，然后通過迭代求最優解，當在限定的時間和迭代次數內目標函數值不再優化時，則認為得到的解為最優解或較優解。具體步驟如下。

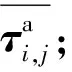
步驟2基因設置。以列車i在區間e(j-1,j)的緩沖時間xi,j-1,j作為基因，因模型僅考慮單線單方向，則基因按順序排列的集合(即染色體)為模型的解集{xi,j-1,j|i∈I,j∈J}。

步驟3求解優化模型。基于式(27)和遺傳算法的求解特點，優化模型又可寫為

(28)

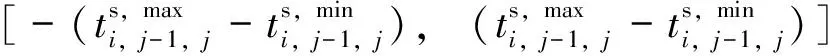
步驟4最優解。在限定的時間或迭代次數內，最優解已收斂且不能更優，則找到最優解的解集{xi,j-1,j,i∈I,j∈J}，運算終止。

4　算　例

北京市城市軌道交通房山線共設有10個車站，列車的技術參數見表1，區間集E的運營參數見表2所示，下行客流OD的到達規律見表3，車站集J中各列車的實際停站時間見表4。選取1 h的研究時段并且針對γ1和γ2取不同值的3個算例，利用Matlab對問題進行描述，并根據本文模型和算法對該線下行列車的運行圖進行魯棒性優化，優化結果見表5。對表5中數據進行絕對值求和，得到表6。

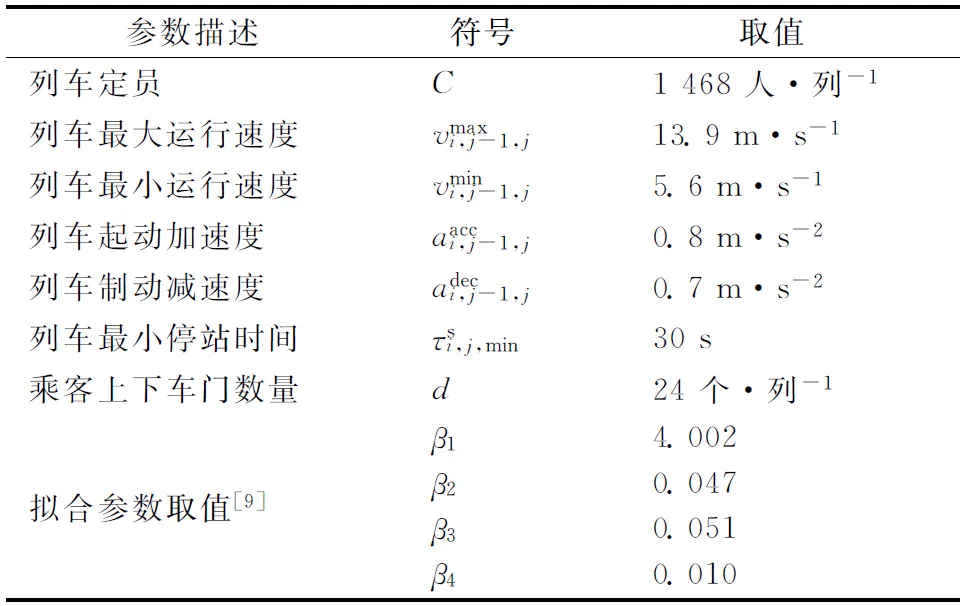
表1　列車技術參數

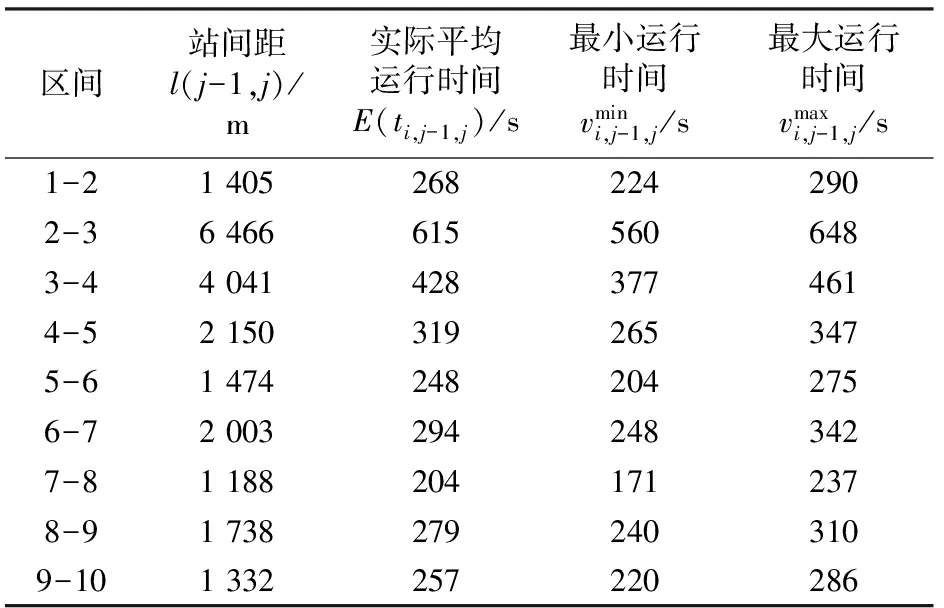
表2　區間集E的運營參數

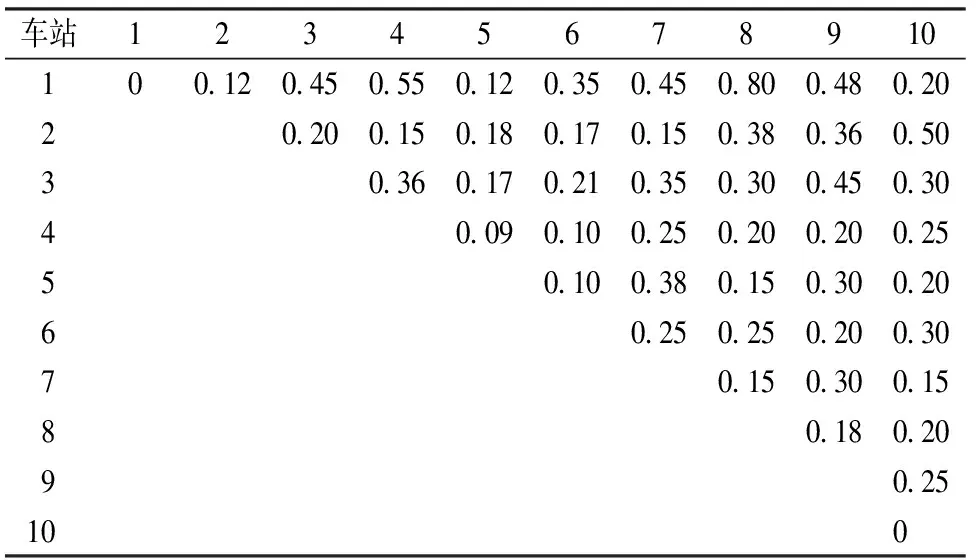
表3　下行客流OD的到達規律　人·s-1

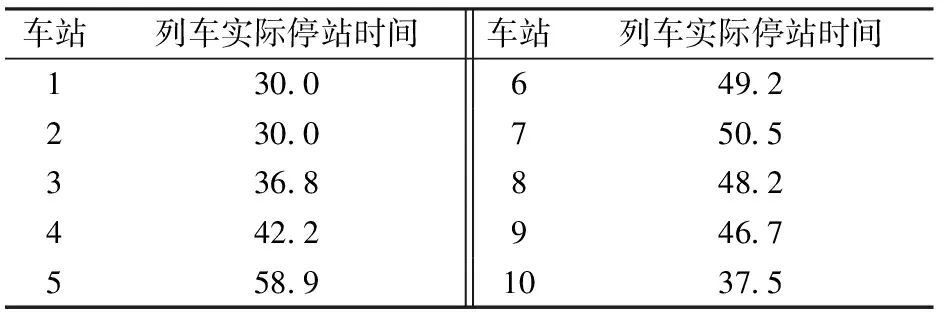
表4　列車在各站停站時間　s

由表5和表6可得出以下結論：

(1)算例1表明模型對發車晚點和發車提前的懲罰一致，列車運行圖魯棒性可恢復時間(以下簡稱：可恢復時間)最短，為209 s，計劃運行的總時間為2 971 s；

(2)算例2表明模型對發車晚點的懲罰小于發車提前，可恢復時間最長，為253 s，但計劃運行的總時間最短，為2 951 s；

(3)算例3表明模型對發車晚點的懲罰大于發車提前，可恢復時間為231 s，但計劃運行的總時間最長，為3 053 s。

表5中的計算結果可直接轉化為該線的列車運行圖或列車時刻表形式。例如，假設列車在始發站(郭公莊站)的出發時刻為15:30:00，則列車時刻表見表7。

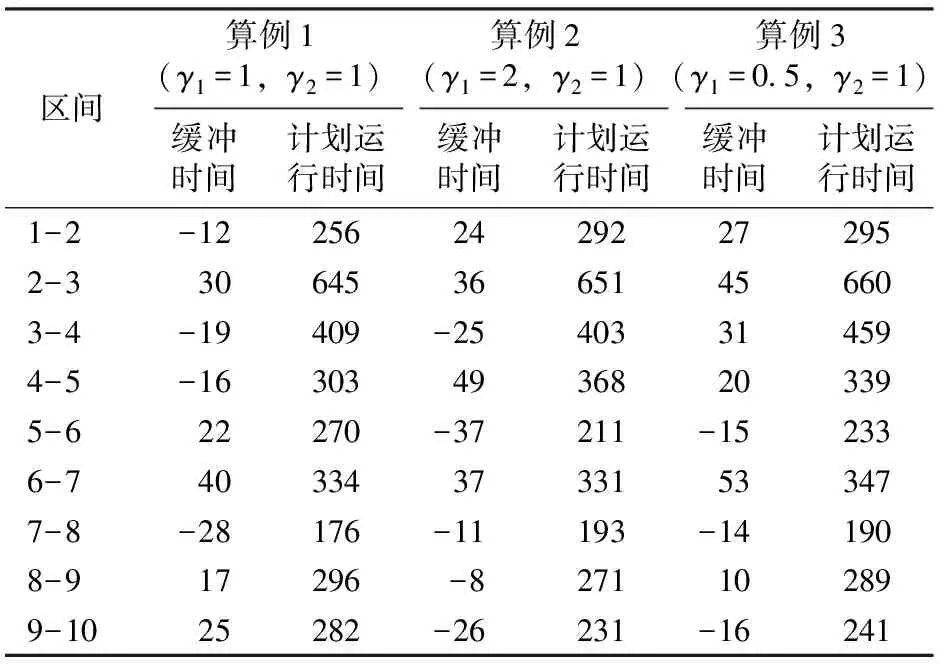
表5　優化結果　s

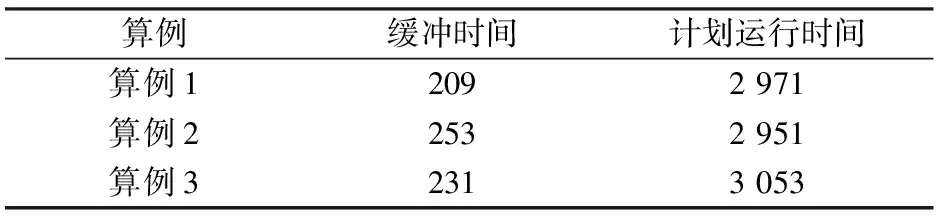
表6　列車運行圖魯棒性恢復時間　s

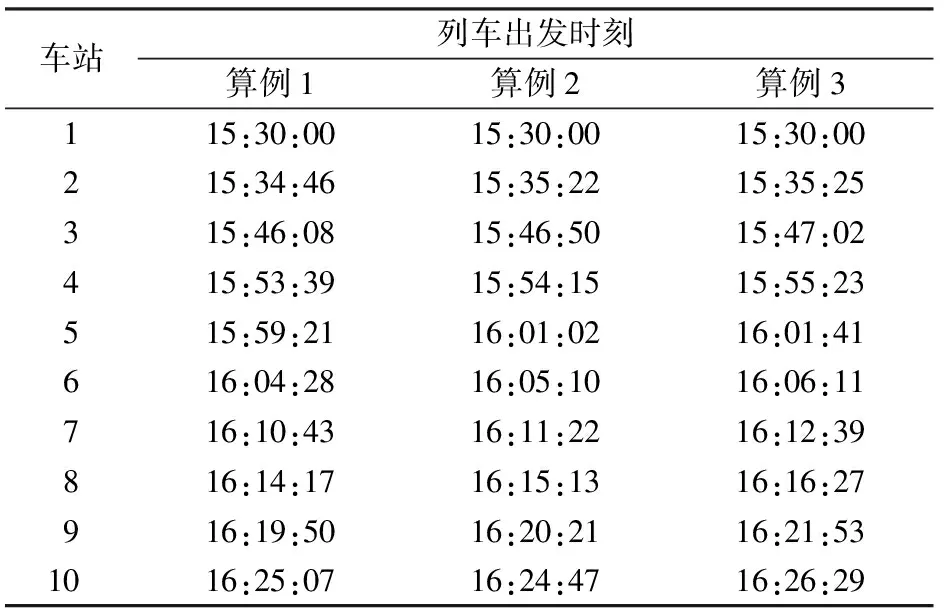
表7　列車時刻表

5　模型的擴展

在城市軌道交通列車運行時段內，可能出現無法保證在每個車站都能準點發車的情況。當運營部門只要求大型樞紐站等重要車站準點發車即可時，本文在既有模型的基礎上，提出“時間控制點法”來實現指定車站發車準點的目標，以提高規定區段內的列車運行圖魯棒性。

時間控制點法的思想是在計劃層同時間軸條件下引入虛擬層，如圖2所示。虛擬層每個時間控制點對應準點率要求高的車站，時間控制點對應的車站集合R?J，旨在形成時間控制點區段內包含多個區間的形式，即列車在時間控制點間的運行時間等于列車在多個區間運行的時間之和。

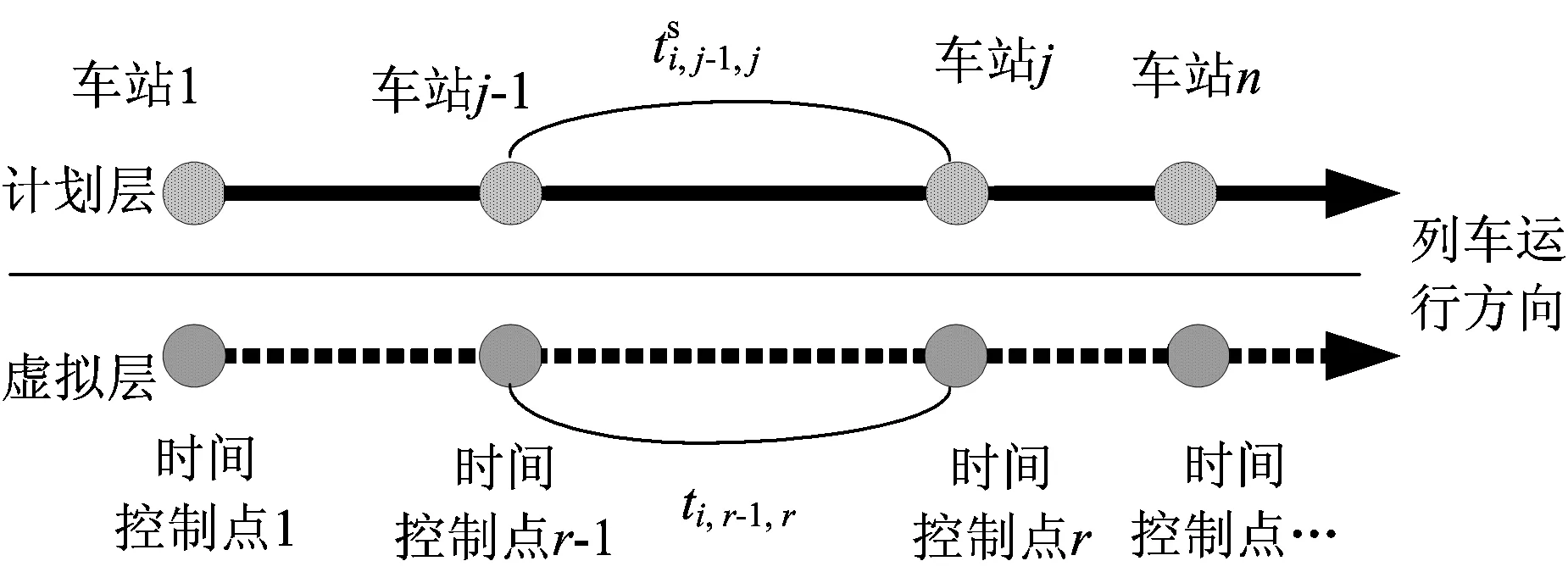
圖2　時間控制點示意圖

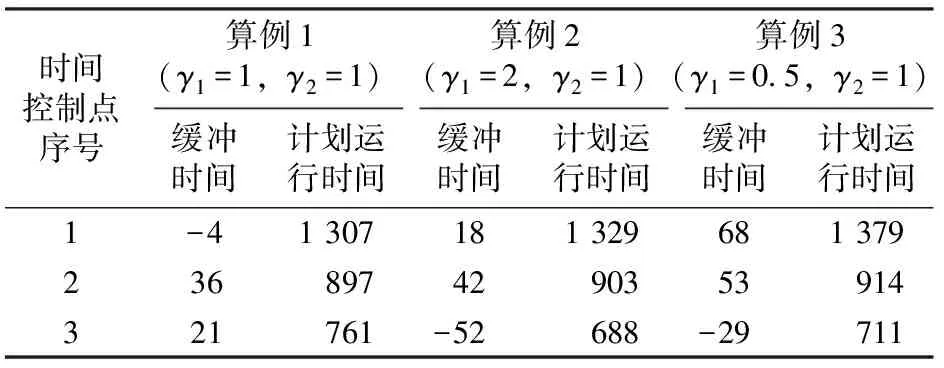
表8　時間控制法的求解結果 s

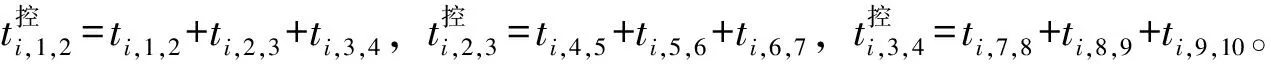
6　結束語

本文以城市軌道交通列車運行圖擾動時間之和最小化為目標，構建了城市軌道交通列車運行圖魯棒性優化模型，通過改進的遺傳算法對問題進行求解。通過模型分析發現，不同懲罰參數的取值對列車運行圖魯棒性的影響較大，需根據實際問題對參數進行標定。以北京市城市軌道交通房山線為例，優化后的列車運行圖有效縮短了總擾動時間，證明了本文方法能夠有效提高列車運行圖的魯棒性。

本文還擴展了城市軌道交通列車運行圖魯棒性優化模型的應用場景，引入時間控制點變量，可實現約束不變的情況下，提高指定車站發車準點率的目標，優化規定區段內的列車運行圖魯棒性。

[1]TAKEUCHI H, GOODMAN C, SONE S.Moving Block Signaling Dynamics: Performance Measures and Re-Starting Queued Electric Trains[J]. IEE Proceedings on Electric Power Applications, 2003, 150(4)：483-492.

[2]汪波, 韓寶明, 戰明輝, 等. 城市軌道交通網絡周期運行圖編制研究[J]. 鐵道學報, 2013, 35(4): 9-15.

(WANG Bo, HAN Baoming, ZHAN Minghui，et al. Study on Formulation of Periodic Train Diagram of Urban Rail Transit Network[J]. Journal of the China Railway Society, 2013, 35(4): 9-15. in Chinese)

[3]聶磊, 張淵, 武鑫. 計算機編制周期性列車運行圖關鍵技術[J]. 中國鐵道科學, 2014, 35(1): 114-121.

(NIE Lei, ZHANG Yuan, WU Xin. Key Technologies for Computer Generation of Cyclic Train Timetable[J]. China Railway Science, 2014, 35(1): 114-121. in Chinese)

[4]江志彬, 徐瑞華, 吳強, 等. 計算機編制城市軌道交通共線交路列車運行圖[J]. 同濟大學學報:自然科學版, 2010, 38(5): 692-696.

(JIANG Zhibin, XU Ruihua, WU Qiang, et al. Shared-Path Routing Timetable Computer Designing in Rail Transit System[J]. Journal of Tongji University:Natural Science, 2010, 38(5): 692-696. in Chinese)

[5]周文梁,史峰, 陳彥,等. 客運專線網絡列車開行方案與運行圖綜合優化方法[J]. 鐵道學報, 2011, 33(2):1-7.

(ZHOU Wenliang, SHI Feng, CHEN Yan, et al. Method of Integrated Optimization of Train Operation Plan and Diagram for Network of Dedicated Passenger Lines[J]. Journal of the China Railway Society, 2011, 33(2):1-7. in Chinese)

[6]劉敏, 韓寶明. 列車運行圖可恢復魯棒性優化模型[J]. 鐵道學報, 2013, 35(10):1-8.

(LIU Ming, HAN Maobing. Recoverable Robust Timetabling Models for Railways[J]. Journal of the China Railway Society, 2013, 35(10):1-8. in Chinese)

[7]YAN Y, MENG Q, WANG S, et al. Robust Optimization Model of Schedule Design for a Fixed Bus Route[J]. Transportation Research Part C: Emerging Technologies, 2012, 25: 113-121.

[8]鄧連波, 曾強, 高偉, 等. 基于彈性需求的城市軌道交通列車開行方案研究[J]. 鐵道學報, 2012, 34(12):16-25.

(DENG Lianbo, ZENG Qiang, GAO Wei, et al. Research on Train Plan of Urban Rail Transit with Elastic Demand[J]. Journal of the China Railway Society, 2012, 34(12):16-25. in Chinese)

[9]WANG Y, DE S B, VAN D B T J J, et al. Efficient Bilevel Approach for Urban Rail Transit Operation with Stop-Skipping[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6):2658-2670.