飛機蒙皮鉚接修理中的鉚釘排布
夏毅銳,韓莉,戴京濤
(海軍航空工程學院青島校區,山東青島266041)
飛機蒙皮鉚接修理中的鉚釘排布
夏毅銳,韓莉,戴京濤
(海軍航空工程學院青島校區,山東青島266041)
對蒙皮鉚接修理中鉚釘排布方式對于修理效果的影響進行研究和分析。在分析以往鉚釘排布方式的基礎上,利用ANSYS軟件對不同鉚釘排布方式的鋁合金板材進行應力分析,并進行實驗驗證,分析鉚釘排布與板材強度之間的關系,最終得出鉚釘排布最佳方案。
鉚接修理;鉚釘排布;有限元
0 前言
飛機的框架是由各種各樣零件組裝而成,鉚釘連接是最常用的裝配工藝之一,盡管鉚釘連接有很多的缺點并且有很多的方法可以替代鉚接(如螺栓連接,焊接,復合材料連接等),但由于鉚接具有連接可靠、質量輕、低成本等優點,因此鉚接仍被廣泛應用于飛機結構的連接中[1-3]。
目前,蒙皮的修理通常采用鉚接修理的辦法,在鉚接修理過程中鉚釘數量和排布方式對于修理的效果有著重要影響,但對于蒙皮鉚接修理的計算公式都是依據材料力學的剪切與擠壓理論,并利用以往的修理經驗進行修正后得到的。針對目前修理工作中還缺乏確定最優鉚釘數量及其排布方法的現狀,通過理論和實驗分析研究鉚釘載荷的傳遞以及載荷的分布規律,從而得出較為合理的鉚釘排布方案。
1 鉚釘排布的相關問題
在飛機的鉚接修理過程中,不僅要保證鉚接構件的強度,還要選擇合適的鉚釘及合理的布置。當鉚釘和構件受力時,鉚釘會產生剪切和擠壓變形。當鉚釘的破壞剪力和破壞擠壓力何一方達到破壞時,另一方的剩余強度都將失去作用。在實際的修理過程中,鉚釘構件的厚度是由幾個構件的厚度疊加在一起的,通常鉚釘的直徑采用公式[4](1)計算。

式中d——鉚釘的直徑
δ——鉚接構件的總厚度
一排鉚釘的中心線與它相鄰另一排鉚釘的中心線之間的距離稱為排距,用a表示;在一排鉚釘中,相鄰的2個鉚釘中心之間的距離,稱為鉚距,用t表示;邊緣一排鉚釘的中心線至構件邊緣的垂直距離,稱為邊距,用c表示(圖1)。
當鉚接構件承受拉力時,板件承受拉力,鉚釘承受剪力,板與鉚釘相互擠壓承受擠壓力,在鉚釘處板還承受剪力。如果鉚釘布置不合理,鉚距過小,板就容易被拉斷;邊距過小,板就容易被剪壞。在實際修理工作中,通常采用公式(2)計算排距、鉚距和邊距[2]。

式中d——鉚釘的直徑
目前在實際修理過程中基本上都是按照這種鉚釘直徑的選擇和鉚釘的排布來進行修理的。公式(2)給出的鉚距是一個大致的范圍,鉚距如何選定會對修理的效果產生很大的影響,并且這還不能保證每次維修的質量,給修理工作埋下了隱患。
2 鉚接板受力分析仿真計算[5]
在鉚接過程中,由于鉚接孔存在的原因,在孔壁附近會產生較高的應力集中,因而鉚釘連接處通常最容易發生破壞。針對于這種情況,對鉚接板應力分布的情況進行軟件仿真計算。
2.1 不同鉚距對板材最大應力的影響
選擇140×50×1.5 mm的2A12板材為研究對象,中心圓孔的直徑為8 mm(這里將中心圓孔假定為板材的破壞區域),一排有2個鉚釘孔,鉚釘孔直徑4 mm,根據公式(2),分別選擇鉚距為12 mm、15 mm、24 mm,對不同鉚距的板材均在板材兩端施加24 MPa的拉力得到的等效應力云圖(圖2~圖4)。
由等效應力云圖可以看處,不同鉚距的板材應力云圖是類似的。其中鉚距為12 mm的板材在右側上方鉚釘孔6點方向位置處應力最大,最大應力SMAX=51.77 MPa;鉚距為15 mm的板材在右側上方鉚釘孔6點方向位置處應力最大,最大應力SMAX= 49.57 MPa;鉚距為24 mm的板材在左側上方鉚釘孔12點方向位置處應力最大,最大應力SMAX=51.83 MPa。
此外,還計算了鉚距為18 mm、21 mm板材的等效應力云圖,根據這些等效應力云圖的最大應力,可以得到不同鉚距排布下板材受到的最大應力曲線圖(圖5)。
通過對不同鉚距的鉚釘排布方案的仿真分析可知,鉚距過大或者過小都不利于修理效果及質量。
2.2 不同直徑的鉚釘孔對板材最大應力的影響
選擇工程中常用的3 mm,3.5 mm鉚釘為研究對象,板材初始條件與2.1中相同,鉚距統一選為15 mm,對不同的鉚釘孔直徑的板材均在板材兩端施加24 MPa的拉力,得到的等效應力云圖(圖6,圖7)。
鉚釘孔直徑3 mm的板材最大應力出現在右側上方鉚釘孔12點方向位置,最大應力SMAX=51.07 MPa;鉚釘孔直徑3.5 mm的板材最大應力出現在右側上方鉚釘孔6點方向位置處應力最大,最大應力SMAX=49.37 MPa。
根據圖3、圖6、圖7可以得到不同直徑鉚釘孔板材的最大應力曲線。圖8。
通過對比不同鉚釘孔直徑對于鉚接板材強度的影響可知,當鉚釘孔直徑為3.5 mm和4 mm時,板材強度相差不大,直徑3.5 mm的鉚釘孔排布略好于直徑4 mm的鉚釘孔排布,這與經驗公式(1)所得到的鉚釘直徑d=3.46 mm是非常接近的。
3 實驗驗證
制作140× 50×1.5mm的2A12試件若干,中心鉆直徑8 mm的圓孔,中心圓孔上下各鉆2個鉚釘孔,試件如圖9所示。本次實驗使用的萬能拉伸試驗機型號為泰斯特WD-P3205,精度等級為1級,最大靜載荷100 kN,速度為0.01~200mm/min。
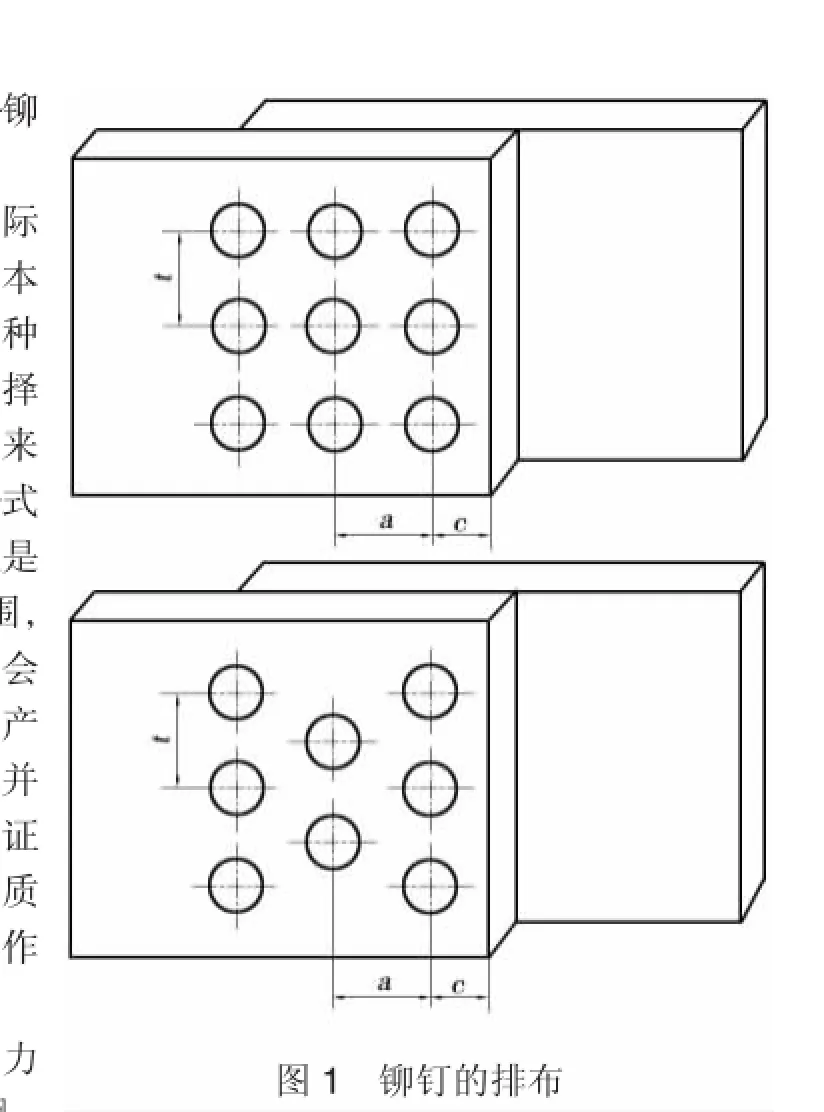
圖1 鉚釘的排布

圖2 鉚釘孔徑4 mm、鉚距12 mm
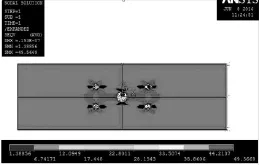
圖3 鉚釘孔徑4 mm、鉚距15 mm
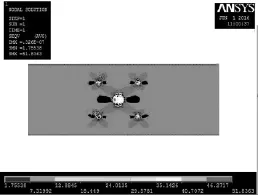
圖4 鉚釘孔徑4 mm、鉚距24 mm
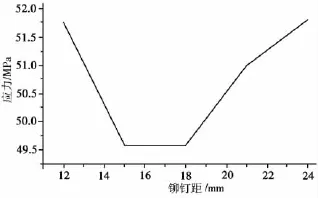
圖5 最大應力與鉚距曲線圖
3.1 鉚釘孔直徑為3 mm的板材實驗結果
制作直徑為3 mm鉚釘孔的試件,鉚距選擇為3~9d,實驗結果如表1。
根據表1的數據得到不同的排布方案(即鉚距的不同)與載荷曲線,圖10。
3.2 鉚釘孔直徑3 mm的板材實驗結果
按照同3.1的鉚釘孔的排布方案保持不變,各組的編號也相應保持不變,只是鉚釘孔直徑變為3.5 mm,通過實驗得到表2中的數據。
根據表2的數據得到不同的排布方案與載荷曲線,圖11。

圖6 鉚釘孔徑3 mm、鉚距15 mm板材的等效應力云圖

圖7 鉚釘孔徑3.5 mm、鉚距15 mm板材的等效應力云圖
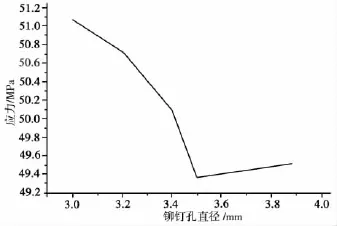
圖8 最大應力與鉚釘孔直徑關系曲線
3.3 鉚釘孔直徑4 mm的板材實驗結果
按照同3.1的鉚釘孔的排布方案保持不變,各組的編號也相應保持不變,只是鉚釘孔直徑變為4 mm,通過實驗得到表3中的數據。
根據表3的數據得到不同的排布方案與載荷曲線,圖12。
根據表2~4中的相關數據可以得知,不同鉚釘直徑大小的排布方案均顯示在鉚距t=6d時,板材所能承受的破壞載荷最大,并且所能承受的載荷比帶中心圓孔板材所能承受的載荷大,這也說明對于一排鉚釘而言最優的鉚距值為6d;由各表中的C,D,E組數據可知對于同一種鉚釘的排布方案而言,當鉚釘直徑為3.5 mm時,板材對應的破壞載荷最大,因此對于板材厚度為1.5 mm的板材,最優的鉚釘直徑為3.5 mm,這與經驗公式(1)和前面有限元仿真得到的結果是一致的。

圖9 實驗板材
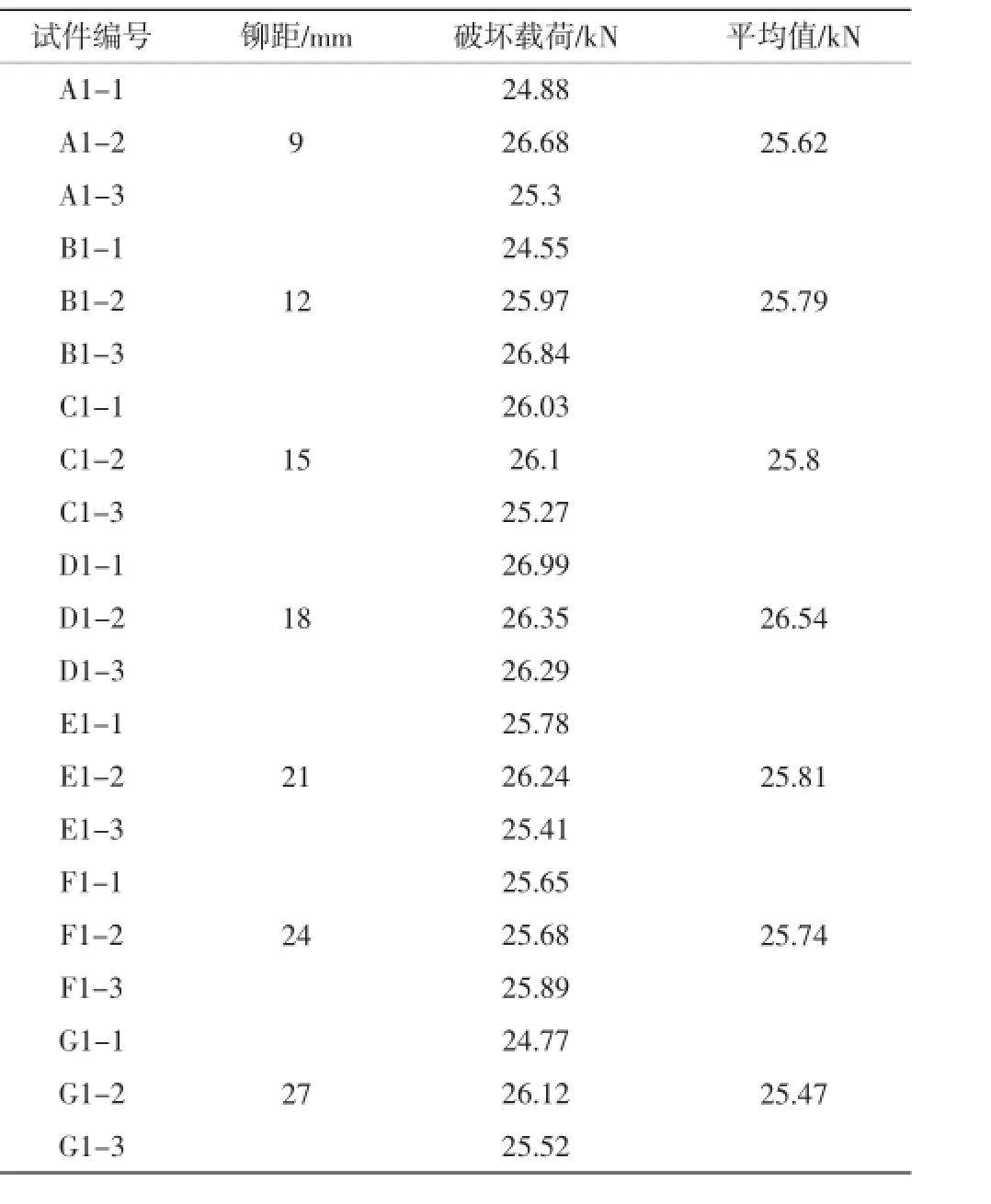
表1 鉚釘直徑3 mm排布方案實驗數據
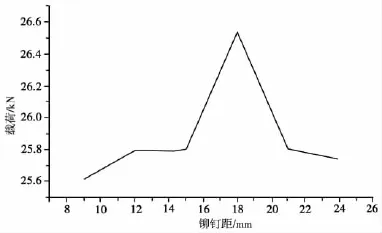
圖10 鉚釘孔直徑3 mm的鉚距與載荷曲線
4 結論
蒙皮鉚接修理過程中,鉚釘的布局形式對提高飛機結構性能和保證鉚接連接件的質量有重大意義。基于ANSYS軟件的基礎上,對鉚釘的相關排布方案進行理論分析與實驗驗證。可知經驗公式得到的鉚釘直徑與有限元計算、實驗驗證得到的結果一致,對于單排鉚釘的最優排布方案為鉚距t=6d時,此時板材的抗拉強度最大,且優于帶破孔板材,因此鉚接修理的效果最好。通過實驗數據分析所得基本與ANSYS軟件所得的結果吻合,這也說明了軟件仿真的可信度較高。本文只是對最簡單鉚釘排布方案進行了實驗驗證和理論分析,缺少對某些復雜情況下鉚釘排布的分析。下一步研究需要對各種復雜情況下鉚釘的相關排布問題進行分析。
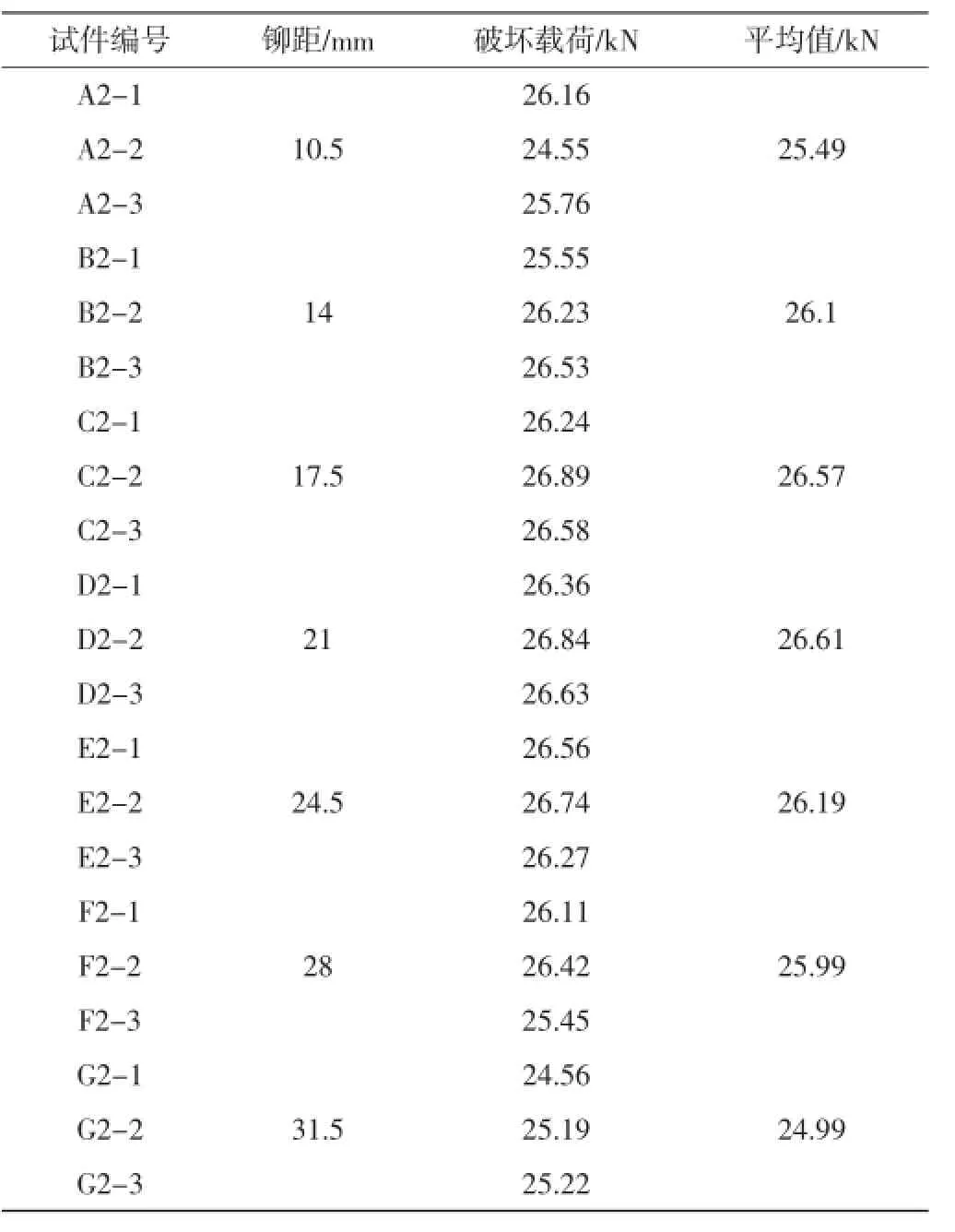
表2 鉚釘直徑3.5 mm排布方案實驗數據
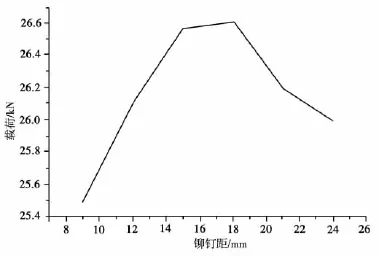
圖11 鉚釘孔直徑3.5 mm的鉚距與載荷曲線
[1]陳福玉.航空鉚接連接件疲勞壽命研究[D].南京:南京航空航天大學,2011.
[2]張洪雙.鉚接工藝參數分析[J].機械設計與制造,2011(6):241-243.
[3]Nanjiang Chen,Richard Ducloux,Christel Pecqu et al.Numerical and Experimental Studies of the Riveting Process[J].International Journal of Material Forming,2011(4):45-54.
[4]胡芳友,戴京濤.飛機結構損傷修理[M].北京:兵器工業出版社,2011.
[5]夏建芳,葉南海.有限元法原理與ANSYS應用[M].北京:國防工業出版社,2011,(10).
〔編輯 王永洲〕

表3 鉚釘直徑4 mm排布方案實驗數據
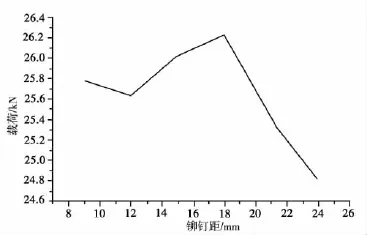
圖12 鉚釘孔直徑4 mm的鉚距與載荷曲線
10.16621/j.cnki.issn1001-0599.2017.03.50
E237
B

