復數域上具有主生成元的四維結合代數的分類

李長洲,李海洋

(西安工程大學理學院，陜西西安 710048)

復數域上具有主生成元的四維結合代數的分類

李長洲,李海洋

(西安工程大學理學院，陜西西安 710048)

為了給出復數域C上的具有主生成元的四維結合代數在同構意義下的分類，利用環論的相關知識以及主生成元所滿足的方程的根的分布:有1個四重根、有4個不同的根、有1個三重根和1個單根、有2個不同的二重根、有1個二重根和2個不同的單根的情況，把主生成元所滿足的以上每一類方程經過平移，拉伸變成較為簡單的形式，采用線性代數與商代數的相關知識以及用maple軟件進行了大量運算得出以上每類方程所表示的同構型與方程的參數選取無關，最后通過比較每類方程所代表的同構型，給出了完整的分類結果，加深了對結合代數結構的理解，對相關的研究具有一定的參考價值。

環論；結合代數；商代數；具有主生成元的四維結合代數；同構分類

抽象代數學研究的一個中心任務是對各種代數結構做同構意義下的分類。例如，有限單群的分類[1]，主理想整環上有限生成模的結構定理[2]等。結合代數[3-6]這種結構早在凱萊提出矩陣代數時就已經有人開始研究，目的是刻畫各種結合代數的結構和表示。低維結合代數[7-15]的研究一直是大家關注的一個熱門課題，文獻[16]研究了代數閉域K上的二維結合代數的分類，具體結果如下：在該結合代數上存在一組基底{e,u}，滿足u2=u或者u2=0。文獻[17]研究了域K上三維結合代數的分類，文獻[18]研究了代數閉域上三維非交換代數的分類，文獻[19]研究了Fp域上的四維結合代數的分類，文獻[20]研究了代數閉域上的含幺元的五維結合代數的分類。

本文對復數域C上具有主生成元的四維結合代數做出分類，這種代數結構取決于主生成元滿足的方程f(x)=x4-px3-qx2-rx-s=0的根的情況，由代數學基本定理知該方程有4個根，由于存在重根，此方程的根一共有5種情況：有1個四重根；有4個不同的根；有1個三重根和1個單根；有2個不同的二重根；有1個二重根和2個不同的單根。

1 背景知識

定義1[4]設M是域K上的向量空間，又在M上定義了一個乘法運算，稱M是域K上的結合代數， 當M滿足以下條件，?α,β,γ∈M,k∈K有：

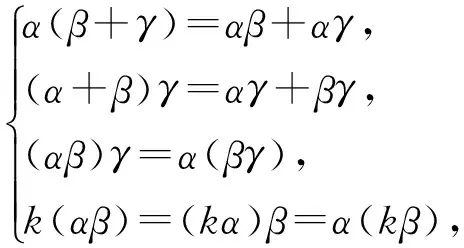
當M中乘法運算滿足交換律時，即?α,β∈M，有αβ=βα，稱M是交換結合代數。當存在元素e∈A，?α∈A，有eα=αe=α，稱e是M中的幺元，M是含幺元的結合代數。

定義2[4]向量空間M的維數稱為域K上的結合代數M的維數。

定義4[4]設M1和M2是域K上的結合代數，稱M1同構于M2，記為M1?M2，當存在一個從M1到M2的線性同構φ，滿足?α,β∈M有φ(αβ)=φ(α)φ(β)。

定義5[4]設M是域K上的含幺元e的四維結合代數，如果在M存在一個元素α，使得e,α,α2,α3是M的一組基底，稱α是主生成元，M是含主生成元的結合代數。這時有α4=pα3+qα2+rα+se,p,q,r,s∈K，顯然M是交換的。

引理1 設M1和M2是域K上的具有主生成元的結合代數，若存在主生成元滿足相同的方程，則M1?M2。

2 坐標變換下的粗分類

筆者利用簡單的線性變換對復數域上四維具有主生成元的代數M進行粗分類，設α∈M，使得e,α,α2,α3線性無關，則α是主生成元，后面用1表示e。設x4=px3+qx2+rx+se是α滿足的方程，即α滿足方程f(x)=x4-px3-qx2-rx-s=0。

1)當f(x)=0有1個四重根a，即f(x)=(x-a)4=0，a∈C。令x′=x-a，顯然1,x′,x′2,x′3也是M的一組基底，這是因為

由于過渡矩陣可逆，所以1,x′,x′2,x′3是M的一組基底，因此x′也是M的主生成元，由上述知x′4=0，仍用x來表示主生成元，這時的代數記作M1，則M1=C[x]/(x4)。

2)當f(x)=0有1個三重根a和1個單根b，即f(x)=(x-a)3(x-b)=0，a≠b，a,b∈C。

由于過渡矩陣可逆，所以1,x′,x′2,x′3是M的一組基底。由上述可得x′3(x′-1)=0。仍用x來表示主生成元，此時的代數記作M2，則M2=C[x]/(x3(x-1))。

3)當f(x)=0有2個不同的二重根a,b，即f(x)=(x-a)2(x-b)2=0,a,b∈C。

4)當f(x)=0有1個二重根a和2個單根b,c，即f(x)=(x-a)2(x-b)(x-c)=0,a,b,c∈C。

5)當f(x)=0有4個不同的根a,b,c,d，即f(x)=(x-a)(x-b)(x-c)(x-d)=0，a,b,c,d∈C。

綜合上面的討論可知4)和5)可能由于d,f的不同取值存在不同的同構類型，所以需要進一步的討論。

3 可能的分類代表元

引理2C[x]/(x2(x-1)(x-a))?C[t]/(t2(t-1)(t+1))，a≠0,1。

證明 令φ:C[x]/(x2(x-1)(x-a))→C[t]/(t2(t-1)(t+1)),

可以驗證φ(x2(x-1)(x-a))=0成立，則該定義是好的，容易看出φ是同態。

設T是從基底1,x,x2,x3到1，t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出：

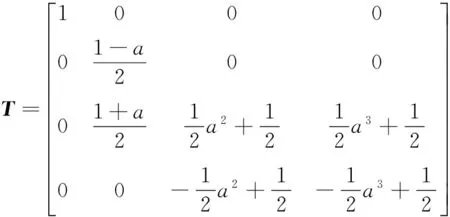
引理3C[x]/(x(x-1)(x-a)(x-b))?C[t]/(t(t-1)(t+1)(t-d))，且C[t]/(t(t-1)(t+1)×(t-d))的同構型與d取值無關，只要d≠0,±1,a≠b且a,b≠0,1。

證明 令φ:C[x]/(x(x-1)(x-a)(x-b))→C[t]/(t(t-1)(t+1)(t-d))，

可以驗證有φ(x(x-1)(x-a)(x-b))=0成立，則該定義是好的，容易看出φ是同態映射。設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

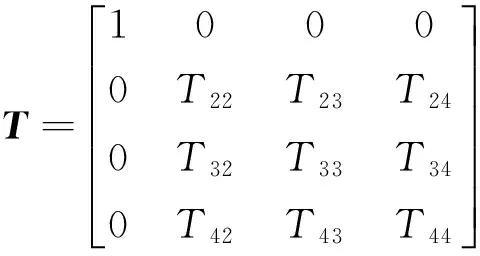
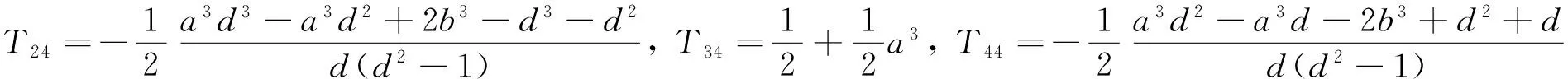
下面證明C[t]/(t(t-1)(t+1)(t-d))的同構型與d取值無關，只要d≠0,±1。

令φ:C[x]/(x(x-1)(x+1)(x-d1)) →C[t]/(t(t-1)(t+1)(t-d2))，d1≠d2，

可以驗證有φ(x(x-1)(x+1)(x-d1))=0，則該定義是好的，容易看出φ是同態。

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出：

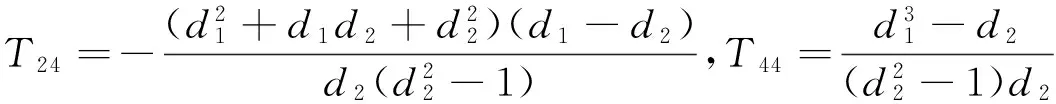
4 分類代表元

定理1M2與M4同構。

證明 令φ:C[x]/(x3(x-1))→C[t]/(t2(t+1)(t-1)),

定理2M1與M2不同構。

證明 若M1與M2同構，則存在一個同構映射:

φ:C[x]/(x3(x-1))→C[t]/(t4),

從而0=φ3(x)(φ(x)-1)=(At3+Bt2+Ct+D)3(At3+Bt2+Ct+D-1)，化簡可得：

4AD3+12BCD2+4C3D-3AD2-6BCD-C3=0,

(1)

4BD3+6C2D2-3BD2-3C2D=0,

4CD3-3CD2=0,

(2)

D4-D3=0。

(3)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

又det(T)=C6，由式(3)得D=0，或D3=1。當D=0時，代入式(1)得出C=0；當D3=1，給式(2)兩邊乘D，把D3=1代入該式得到C=0，綜上C=0，可知φ不是同構映射，從而M1與M2不同構。

定理3M1與M3不同構。

證明 若M1與M3同構，則存在一個同構映射：

φ:C[x]/(x2(x-1)2)→C[t]/(t4)，

從而0=φ2(x)(φ(x)-1)2=(At3+Bt2+Ct+D)2(At3+Bt2+Ct+D-1)2，化簡得：

4AD3+12BCD2+4C3D-6AD2-12BCD-2C3+2AD+2BC=0，

(4)

4BD3+6C2D2-6BD2-6C2D+2BD+C2=0，

4CD3-6CD2+2CD=0，

D4-2D3+D2=0，

(5)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

又det(T)=C6，由式(5)可得D=0,1,當D=0代入式(4)得C=0，當D=1代入式(4)得C=0，綜上C=0，可知φ不是同構映射，從而M1與M3不同構。

定理4M1與M5不同構。

證明 若M1與M5同構，則存在一個同構映射：

φ:C[x]/(x(x-1)(x+1)(x-2))→C[t]/(t4)，

從而有：

0=φ(x)(φ(x)-1)(φ(x)+1)(φ(x)-2)=

(At3+Bt2+Ct+D)(At3+Bt2+Ct+D-1)(At3+Bt2+Ct+D+1)(At3+Bt2+Ct+D-2)，

化簡得：

4AD3-6AD2+12BCD2-12BCD+4C3D-2C3-2AD+2A-2BC=0，

4BD3-6BD2+6C2D2-6C2D-2BD+2B-C2=0，

4CD3-6CD2-2CD+2C=0，

(6)

D4-2D3-D2+2D=0，

(7)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出：

又det(T)=C6，由式(7)得D=0,±1,2，代入式(6)得C=0，可知φ不是同構映射，從而M1與M5不同構。

定理5 M2與M3不同構。

證明 若M2與M3同構，則存在一個同構映射：

φ:C[x]/(x3(x-1))→C[t]/(t2(t-1)2)，

從而有0=φ3(x)(φ(x)-1)=(At3+Bt2+Ct+D)3(At3+Bt2+Ct+D-1)，化簡得：

10A4+36A3B+32A3C+28A3D+48A2B2+84A2BC+72A2BD+36A2C2+60A2CD+24A2D2+28AB3+72AB2C+60AB2D+60ABC2+96ABCD+36ABD2+16AC3+36AC2D+24ACD2+4AD3+6B4+20B3C+16B3D+24B2C2+36B2CD+12B2D2+12BC3+24BC2D+12BCD2+2C4+4C3D-7A3-18A2B-15A2C-12A2D-15AB2-24ABC-18ABD-9AC2-12ACD-3AD2-4B3-9B2C-6B2D-6BC2-6BCD-C3=0，

(8)

-9A4-32A3B-28A3C-24A3D-42A2B2-72A2BC-60A2BD-30A2C2-48A2CD-18A2D2-24AB3-60AB2C-48AB2D-48ABC2-72ABCD-24ABD2-12AC3-24AC2D-12ACD2-5B4-16B3C-12B3D-18B2C2-24B2CD-6B2D2-8BC3-12BC2D+4BD3-C4+6C2D2+6A3+15A2B+12A2C+9A2D+12AB2+18ABC+12ABD+6AC2+6ACD+3B3+6B2C+3B2D+3BC2-3BD2-3C2D=0，

(9)

4CD3-3CD2=0，

(10)

D4-D3=0。

(11)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

T13=D2,T23=2CD,T33=-3A2-4AB-2AC-B2+2BD+C2,T43=4A2+6AB+4AC+2AD+2B2+2BC，T14=D3,T24=3CD2,T34=-6A3-15A2B-12A2C-9A2D-12AB2-18ABC-12ABD-6AC2-6ACD-3B3-6B2C-3B2D-3BC2+3BD2+3C2D，T44=7A3+18A2B+15A2C+12A2D+15AB2+24ABC+18ABD+9AC2+12ACD+3AD2+4B3+9B2C+6B2D+6BC2+6BCD+C3。

由式(11)得D=0,1。

當D=1時，代入式(10)得C=0，代入det(T)=C(3A+2B+C)(C+A+B)4=0。

當D=0時，代入式(8)化簡得：

(10A2+16AB+12AC+6B2+8BC+2C2-7A-4B-C)(C+B+A)2=0。

把D=0代入式(9)化簡得：

-(9A2+14AB+10AC+5B2+6BC+C2-6A-3B)(C+B+A)2=0。

當A+B+C=0時，det(T)=C(3A+2B+C)(C+A+B)4=0。

當A+B+C≠0時，要使得上述兩式為零，要滿足：

10A2+16AB+12AC+6B2+8BC+2C2-7A-4B-C=0，

(12)

-9A2-14AB-10AC-5B2-6BC-C2+6A+3B=0，

(13)

式(12)+式(13)可得：

10A2+16AB+12AC+6B2+8BC+2C2-7A-4B-C+

(-9A2-14AB-10AC-5B2-6BC-C2+6A+3B)=

A2+2AB+2AC+B2+2BC+C2-A-B-C=

(C+B+A)(C-1+B+A)，

取C=1-A-B代入式(12)得2A+B+1，代入式(13)得-2A-B-1。聯立方程：

2A+B+1=0；A+B+C=1，

解出A=C-2,B=-2C+3，代入det(T)=C(3A+2B+C)(C+A+B)4=0，綜上得到M2與M3不同構。

定理6 M2和M5不同構。

證明 若M2和M5同構，則存在一個同構映射：

φ:C[x]/(x(x-1)(x+1(x-2))→C[t]/(t3(t-1))，

從而有：

0=φ(x(x-1)(x+1)(x-2))=φ(x)(φ(x)-1)(φ(x)+1)(φ(x)-2)=

(At3+Bt2+Ct+D)(At3+Bt2+Ct+D-1)(At3+Bt2+Ct+D+1)(At3+Bt2+Ct+D-2)，

化簡得：

A4+4A3B+4A3C+4A3D+6A2B2+12A2BC+12A2BD+6A2C2+12A2CD+6A2D2+4AB3+12AB2C+12AB2D+12ABC2+24ABCD+12ABD2+4AC3+12AC2D+12ACD2+4AD3+B4+4B3C+4B3D+6B2C2+12B2CD+6B2D2+4BC3+12BC2D+12BCD2+C4+4C3D-2A3-6A2B-6A2C-6A2D-6AB2-12ABC-12ABD-6AC2-12ACD-6AD2-2B3-6B2C-6B2D-6BC2-12BCD-2C3-A2-2AB-2AC-2AD-B2-2BC+2A=0，

4BD3+6C2D-6BD2-6C2D-2BD-C2+2B=0，

4CD3-6CD2-2CD+2C=0，

(14)

D4-2D3-D2+2D=0，

(15)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

T13=D2,T23=2CD,T33=2BD+C2,T34=A2+2AB+2AC+2AD+B2+2BC，T14=D3,T24=3CD2,T34=3BD2+3C2D,T44=A3+3A2B+3A2C+3A2D+3AB2+6ABC+6ABD+3AC2+6ACD+3AD2+B3+3B2C+3B2D+3BC2+6BCD+C3，又det(T)=C3(A+B+C)3，由式(15)得D=0,±1,2，代入式(14)得C=0，從而φ不是同構映射，即M2和M5不同構。

定理7 M3和M5不同構。

證明 若M3和M5同構，則存在一個同構映射：

φ:C[x]/(x(x-1)(x+1)(x-2))→C[t]/(t2(t-1)2)，

從而有：

0=φ(x(x-1)(x+1)(x-d)=

φ(x)(φ(x)-1)(φ(x)+1)(φ(x)-2)=

(At3+Bt2+Ct+D)(At3+Bt2+Ct+D-1)(At3+Bt2+Ct+D+1)(At3+Bt2+Ct+D-2)，

化簡得：

10A4+36A3B+32A3C+28A3D+48A2B2+84A2BC+72A2BD+36A2C2+60A2CD+24A2D2+28AB3+72AB2C+60AB2D+60ABC2+96ABCD+36ABD2+16AC3+36AC2D+24ACD2+4AD3+6B4+20B3C+16B3D+24B2C2+36B2CD+12B2D2+12BC3+24BC2D+12BCD2+2C4+4C3D-14A3-36A2B-30A2C-24A2D-30AB2-48ABC-36ABD-18AC2-24ACD-6AD2-8B3-18B2C-12B2D-12BC2-12BCD-2C3-4A2-6AB-4AC-2AD-2B2-2BC+2A=0，

-9A4-32A3B-28A3C-24A3D-42A2B2-72A2BC-60A2BD-30A2C2-48A2CD-18A2D2-24AB3-60AB2C-48AB2D-48ABC2-72ABCD-24ABD2-12AC3-24AC2D-12ACD2-5B4-16B3C-12B3D-18B2C2-24B2CD-6B2D2-8BC3-12BC2D+4BD3-C4+6C2D2+12A3+30A2B+24A2C+18A2D+24AB2+36ABC+24ABD+12AC2+12ACD+6B3+12B2C+6B2D+6BC2-6BD2-6C2D+3A2+4AB+2AC+B2-2BD-C2+2B=0，

4CD3-6CD2-2CD+2C=0，

(16)

D4-2D3-D2+2D=0。

(17)

設T是從基底1,x,x2,x3到1,t,t2,t3的過渡矩陣，即φ(1,x,x2,x3)=(1,t,t2,t3)T，可以求出

T13=D2,T23=2CD,T33=-3A-4AB-2AC-B2+2BD+C2,T43=4A2+6AB+4AC+2AD+2B2+2BC，T14=D3,T24=3CD2,T34=-6A3-15A2B-12A2C-9A2D-12AB2-18ABC-12ABD-6AC2-6AC2-6ACD-3B3-6B2C-3B2D-3BC2+3BD2+3C2D，T44=7A3+18A2B+15A2C+12A2D+15AB2+24ABC+18ABD+9AC2+12ACD+3AD2+4B3+9B2C+6B2D+6BC2+6BCD+C3，又det(T)=C(3A+2B+C)(C+A+B)4，由式(17)得D=0,±1,2代入式(16)得C=0，從而φ不是同構映射，即M3和M5不同構。

綜上，復數域C上的含主生成元的結合代數一定是交換的，且在同構意義下只有4類：

M1=C[x]/(x4)； M2=C[x]/(x3(x-1))；

M3=C[x]/(x2(x-1)2)； M5=C[x]/(x(x-1)(x+1)(x-2))。

/

:

[1]ASCHBACHERM.Thestatusoftheclassificationofthefinitesimplegroups[J].NoticeoftheAmericanMathematicalSociety, 2004,51(7):529.

[2] 孟道驥,王立云,史毅茜, 等.抽象代數Ⅰ-代數學基礎[M].北京:科學出版社,2011.

[3] AUSLANDER M. Representation Theory of Artin Algebra[M]. Cambridge: Cambridge University Press, 1993.

[4] 孟道驥,王立云,史毅茜, 等.抽象代數Ⅱ-結合代數[M].北京: 科學出版社,2011.

[5] 陳輝.群的結構與對稱性[M].杭州: 浙江大學出版社,2008.

[6] KENNEDY C. Deep matrix algebras of finite type[J]. Algebras and Reprensentation Theory, 2006, 9(5):525-537.

[7] HUANG Wenxue. A characterization of triangularizability of a linear associative algebra[J]. Linear Algebra and Its Applications,1999,299:165-169.

[8] WEI Changguo. Classification of extension torus algebra Ⅱ[J]. Science China Mathematics, 2012, 55(1) :179-186.

[9] KIRTLAND J. On two classes of finite inseparablep-groups[J]. Acta Mathematica Sinica, 2015, 31(7):1203-1214.

[10]TIMOTHY G. The princeton companion to mathematics[J].Princetion Companion to Mathematics, 2008,4(1):21-24.

[11]HAMILTON W R. On quaternions, or on a new system of imaginaries in algebra[J].Philosophical Magazine, 1844,25(3):489-495.

[12]LUIS A. Classification of some graded not necessarily associative division algebras Ⅰ[J]. Communications in Algebra, 2014, 42 (12):5019-5049.

[13]DROZD Y A, KIRICHENKO V V. Finite Dimensional Algebras[M]. NewYork: Springer-Verlag, 1993.

[14]BARNES D W. On (n+2) dimensionaln-Lie algebras[J]. arXiv: 0704,1892.

[15]KORESHKOV N A.Finite-dimensional homogeneously simple algebras of associative type[J].Russian Mathematica,2010,54(9):30-35.

[16]de GRAAF W A.Classification of solvable lie algebras[J].Experimental Mathematics,2005,14(1):15-25.

[17]王頌生,李明楚.域K上三維結合代數的分類[J].江西師范大學學報(自然科學版), 1985(2):23-30.

[18]孫翠芳,程智.代數閉域上三維非交換代數的分類[J].純粹數學與應用數學,2010,26(3):516-519. SUN Cuifang, CHENG Zhi. The claassfications of 3-dimensionally non-commutative algebras on algebraiclly closed field[J]. Pure and Applied Mathematics, 2010, 26(3):516-519.

[19]趙嗣元.域Fp上四維結合代數的同構分類[J].上海師范大學學報(自然科學版), 2001,30(4):28-33. ZHAO Siyuan. Classification of associative algebras of dimension 4 over fieldFp[J]. Journal of Shanghai Teachers University (Natural Sciences), 2001, 30(4): 28-33.

[20]MAZZOLA G. The algebraic and geometric classification of associative associative algebras of dimension five[J]. Manuscripta Mathematica, 1979, 27(1): 81-101.

Classification of 4-dimensional associative algebras with principal generators over complex numbers

LI Changzhou, LI Haiyang

(School of Science, Xi’an Polytechnic University, Xi’an, Shaanxi 710048, China)

In order to obtain the classification of 4-dimensional associative algebras with principal generators over complex numberCunder isostructuralism, by using the ring theory and distribution of roots of the equations satisfied by the principal generators: one quadruple root, four different roots, one triple root and one simple root, two different double roots, one double root and two different simple roots, the above equations are translated and stretched, then the more simple equations are obtained. By using linear algebras, quotient algebras and maple to make a large number of operations, it is concluded that each isomorphism type has nothing to do with parameters. Finally by comparing each isomorphism type, the complete classification is obtained, which deepens the realization of structure of asso ciative algebra, and provides reference for relative study.

ring theory; associative algebras; quotient algebras; 4-dimensional associative algebras with principal generators; isomorphism classification

1008-1542(2017)02-0123-08

10.7535/hbkd.2017yx02002

2016-09-29；

2016-11-28；責任編輯：張 軍

國家自然科學基金(11271297)；西安工程大學研究生創新基金(CX201625)

李長洲(1989—)，男，陜西漢中人，碩士研究生，主要從事拓撲學方面的研究。

李海洋教授。E-mail：fplihaiyang@126.com

O153 MSC(2010)主題分類：34B40

A

李長洲, 李海洋.復數域上具有主生成元的四維結合代數的分類[J].河北科技大學學報,2017,38(2):123-130.

LI Changzhou, LI Haiyang.Classification of 4-dimensional associative algebras with principal generators over complex numbers[J].Journal of Hebei University of Science and Technology,2017,38(2):123-130.