人教版三種教材中“圓”的比較與思考

葉妙法

摘 要 本文以人教版1990年、2006年、2011年（新課標）的三種小學數學教材中“圓”的課程內容為研究對象，從內容呈現形式及順序的視角出發，對“圓”的教材安排、教材結構、情境設計、概念得出、畫圓技能、知識拓展等進行比較分析，并結合自己教學實踐，闡釋了對概念課教學的一些思考與想法。

關鍵詞 圓 小學數學 人教版教材 比較

中圖分類號：G623.5 文獻標識碼：A 文章編號：1002-7661（2017）07-0063-03

不同時期的小學課本，反映不同時代的教學理念。尋求不同時代背景下的教材特點，比較不同時期的教材編排，可以從一個側面了解教學理念的變化過程，從中看到一些教學方式、學習方式、思維方式等諸多層面的進步與發展，為我們一線教師更好地使用教材起到積極的作用。現筆者選取人民教育出版社（以下簡稱“人教版”）1990年、2006年、2011年（新課標）出版的三種小學數學教材，對“圓”的課程內容進行比較分析。

一、“圓”的教材年級安排比較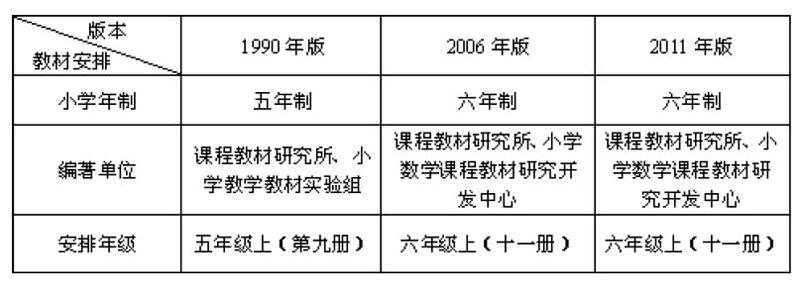

三個時期的教材把“圓”的教學都安排在小學的最后一年學習。之所以把“圓”的相關知識的學習放在最后一年學習，主要是考慮到有關圓的教學內容對學生來說有一定的難度，知識點也滲透了曲線圖形與直線圖形的關系，從空間觀念方面來說，學生已經進入了一個新的領域，也是小學數學教學中的重難點。而且“圓的周長”、“圓的面積”對學生來說不容易想到化曲為直的過程，因此，根據學生的年齡特征安排在最后一年比較合理，這樣相對來說學起來比較輕松，也可以為學習圓柱、圓錐等知識打好基礎。

二、“圓”的教材結構比較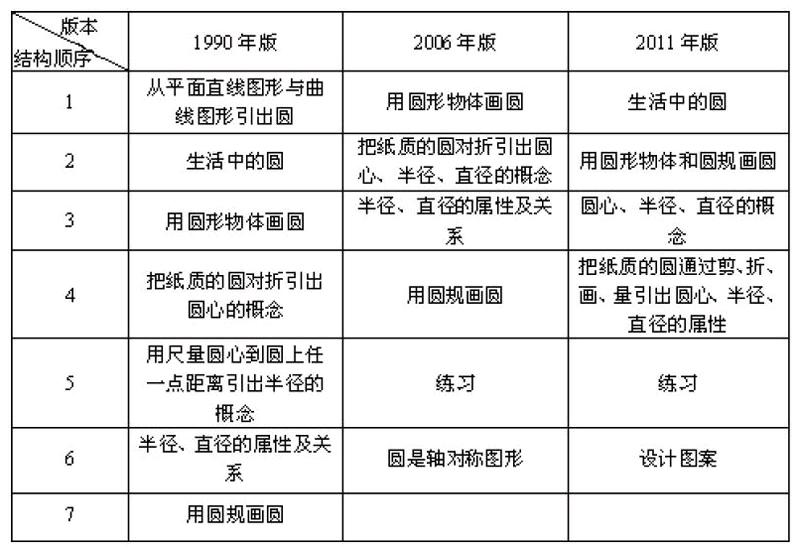

從上面三種教材的結構上看，在知識呈現的前后順序大致一樣，但也存在共同點與不同點。它們的共同點是：先畫圓再給出圓的各部分名稱，再進行半徑、直徑的屬性與關系研究。不同點是：（1）1990年版與2011年版的教材在給出圓的各部分名稱前，讓學生回顧生活中的圓以及畫圓，而2006年版的教材在給出圓的各部分名稱之前，沒有“生活中的圓”這一環節。（2）1990年版和2006年版的教材是在認識了圓的各部分名稱、概念、關系后再“用圓規畫圓”，而2011年版的教材把“用圓規畫圓”和“用圓形物體畫圓”結合起來作為學生探索的環節，并放在“認識圓的各部分名稱”之前，這樣的安排更注重解決問題策略的多樣化以及注重探索的過程。

三、“圓”的情境設計比較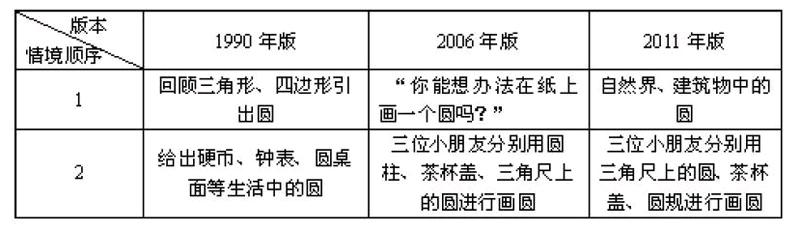

從三個不同版本的教材情境設計來看，它們都考慮到了“生活中的圓”，這樣的情境比較符合學生的實際。不過它們也有不同點：（1）1990年版“生活中的圓”是直接用文字表現出來，教材上直接寫著“我們周圍的物體有很多是圓形的。例如硬幣、鐘面、圓桌面等”，然后在文字下面附上三張圖，而2006年版及2011年版就沒有直接出現這樣的文字，2006年版是在主題圖中讓學生通過畫圓感受“生活中的圓”，2011年版是通過尋找生活中的圓和畫圓兩個情境來感受“生活中的圓”。（2）雖然三種版本都強調了圓是生活中常見的圖形，但1990年版是通過與三角形、四邊形等平面圖形進行比較引出另一個平面圖形圓，而2006年版和2011年版都強調學生自己去尋找發現生活中的圓，充分調動學生在生活中認識圓的經驗。

四、“圓”的概念得出比較

雖然三種都重視圓心、半徑與直徑這三個概念的發生過程，也在概念得出之前注重學生的活動過程，如1990年版的和2006年版的教材都讓學生折一折，2011年版的教材讓學生畫一畫，這樣的活動設計為學生對概念的理解起到良好的保障作用。但它們的概念得出存在著較大的差異，1990年版的教材是操作得出圓心、半徑的概念，直接定義直徑概念，并著重探索半徑與直徑之間的關系；2006年版的教材是操作得出圓心、半徑以及直徑的概念，著重探索半徑和直徑之間的關系；2011年版的教材是直接定義圓心、半徑、直徑的概念，著重探索圓的畫法及概念之間的關系。教材編排的改變是把“概念的探索”轉變為“知識的探索”，更有利于學生探索與發現概念的本質與概念之間的聯系。

五、“圓”的圓規畫圓比較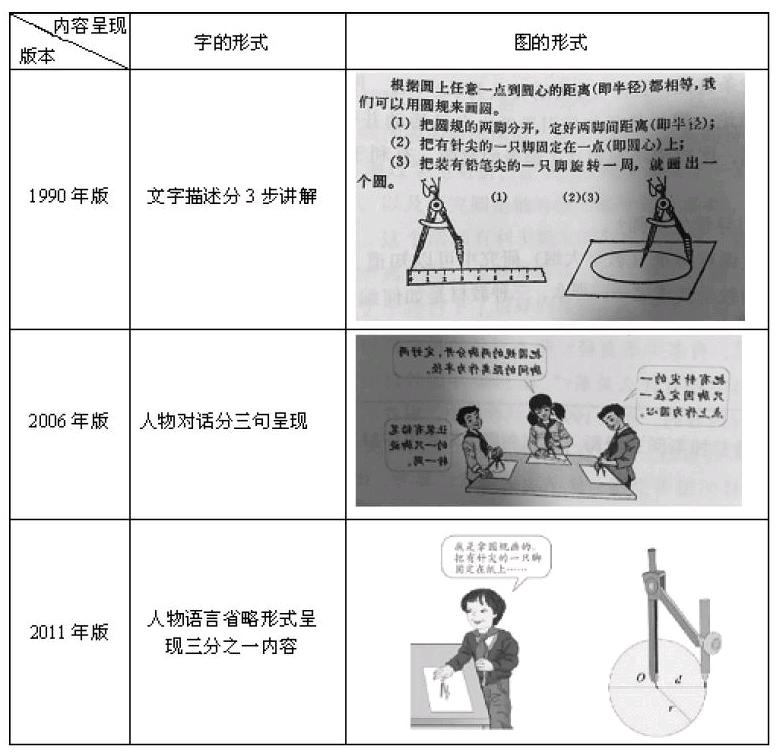

1990年版的教材明確闡述了用圓規畫圓的原理：根據圓上任意一點岙圓心的距離（即半徑）都相等，而且十分明確地闡述了用圓規畫圓的步驟及給出了相對應的圖示；2006年版的教材以人物對話的形式給出了畫圓的步驟，給出的圖示相對比較簡單；2011年版的教材對如何用圓規畫圓沒有給出詳細的步驟，只是給出部分的暗示。教材這樣的變化，或許是想讓學生自己總結提煉出畫圓的方法與步驟，而不是老師把步驟教給學生，體現學生的主體性與發展性。不過依筆者在教學中的經驗，若在教學中最終形成如何用圓規畫圓的步驟，會更加有利于學生掌握畫圓的技能。

六、“圓”的知識拓展比較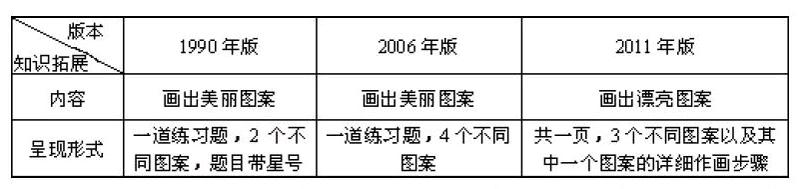

這用運用圓規和直尺設計圖案是一種很好的作業形式，一方面可以運用圓的知識，進一步熟練畫圓的技能，另一方面可以培養學生的學習興趣和創造精神，不過三中版本的拓展程度不同。首先從題目的要求來看，被打星號的練習題表示是選做題，并不要求所有的學生都掌握，所以2006年版的和2011年版的在作圖要求上比1990年版的要高；2011年版的圖案雖然比2006年版的少了一個，但篇幅增大，而且有詳細的步驟，顯然在表述一個數學問題時，2011年版的難度相對較低，學生容易解決。從這里看出，教材考慮到圓的相關知識拓展的廣度與深度，設計的練習如何更有利于學生學習。

七、對“圓”的思考

通過對人教版不同版本教材中關于“圓”的內容整理、分析與比較，發現不管在哪個版本的教材中，“活動”是概念課教學的導入，“過程”即學習，最后在“圖式”中獲得概念，這樣一個過程，就是我們平常概念課的一種常態教學環節，這樣的環節為的就是讓學生充分經歷“概念的產生”、“概念的形成”、“概念的應用”整個過程，而這個過程筆者認為是數學思維的過程，要具有表象性、概括性、問題性的數學思維。

（一）概念課要具表象性

數學概念是事物本質屬性的一種反映，它是一種客觀事物的特征概括，所以有時需要明確的含義。如果學生對一些概念含義不明白，那么在他們解決問題時一定會遇到困難。因此讓概念表象可以讓學生直接作用于感覺器官，更加有利于對概念的理解。如1990年版的“圓”就有半徑與直徑關系的圖式表象：d=2r或r=1/2d，2006年版與2011年版也是用字母d、r來表示。這樣的字母、式子可以讓學生對半徑與直徑的關系與公式的結構關系形成相一致的模式映象。

（二）概念課要具概括性

數學中很多概念是比較抽象的，如“同一圓內，所有的半徑都相等，所有的直徑都相等”這一結論概括，對于學生來說是將活動中直徑與半徑之間的聯系推廣到所有圓中去，這種思維概括與抽象互為表里的描述更需準確性，因此，我們要得出明確的概括性語言。1990年版的教材是以提問的形式：“在一個圓里，直徑的長度與半徑有什么關系？”而2006年版和2011年版的教材就明確用文字概括出：“同一圓內，所有的半徑都相等，所有的直徑都相等”，再讓學生進一步想象、推理、感悟這一結論。

（三）概念課要具問題性

解決問題是數學思維活動的中心，美國數學家哈默爾莫斯指出：定理、證明、概念、定義、理論、公式、方法中任何一個都不是數學的心臟，只有問題是數學的心臟。概念的學習也是為了讓學生更好地解決問題，所以概念課更應具有問題性。從2006年版和2011年版的教材來看，它們都有“你能在紙上畫一個圓嗎？”這樣一個圍繞問題展開的思維活動，三個版本也同時都有“設計美麗圖案”的習題，表現為“發現問題—提出問題—分析問題—解決問題”的一般思維過程。

所以，概念課的教學要揭示或展現蘊含在知識里的本質，作為老師，我們要分析教學內容的特定含義，要分析教材編者的數學思維過程，要揭示教材編寫者的具體意圖。我們若能橫向比較教材的安排，縱向比較教材的變化，努力讀懂教材、用好教材，我們在教學上將會游刃有余。

參考文獻：

[1]朱樂平. 圓的認識教學研究[M].北京：教育科學出版社，2013 .

[2]教育部.義務教育數學課程標準（2011版）解讀[M].武漢：湖北教育出版社，2011.

[3]朱學堯.簡單的設計，精彩的演繹——觀潘小明老師的“圓的認識”一課[J].小學教學（數學版），2011，（04）.

（責任編輯 楚云鵬）