雙臂電橋測低值電阻的等/非等精度測量不確定度評定

張莎+張怡+海蓮+張歡

摘 要 以雙臂電橋測低值電阻電阻率的實驗數據處理為例，本文研究等精度測量的不確定度評定方法及非等精度測量的兩種不確定度評定方法，探討不等精度測量中B類不確定度對處理結果的影響。并且給出了針對具有兩個線性變量而其它待測量真值不變的多待測量實驗的不確定度的直線擬合法，且由實驗數據的對比分析表明了其合理性和準確性。

【關鍵詞】雙臂電橋 等精度測量 非等精度測量 不確定度評定

1 引言

直流雙臂電橋測低值電阻電阻率是一個廣泛開展的綜合性大學物理實驗，其不同于中學的測量電阻的方法和對間接測量量的不確定度評定對引導學生理解大學物理和中學物理的異同上發揮著重要作用；對開拓學生的物理思維和啟發學生運用不同方法測量物理量方面具有重要的意義。在雙臂電橋測電阻時可以采用電阻長度不變的等精度測量和電阻長度變化的非等精度測量（廣義的非等精度測量）兩種方案。對不同方案，處理不確定度時應該選擇不同的處理方法。等精度測量數據的不確定度有各類教材和參考書可做參考；部分論文對其它實驗的非等精度的不確定度進行了處理，但不同的不確定度處理方法的結果之間或者非等精度和等精度測量的處理結果間的比較存在較大差異，而本實驗非等精度測量的不確定度評定卻未見提及。但我們在開展該實驗時統計發現，在同學們自由選擇的情況下，有超過2/3的學生會選擇非等精度測量；而即便是在刻意引導下，也有接近1/4的學生采用非等精度測量。在處理不確定度時，絕大多數的學生卻使用了間接測量量的等精度不確定度評定方法，這導致大部分采用非等精度測量方案的同學處理的不確定結果不合理。可見本實驗中，非等精度的不確定度評定是不可避免的內容。為此，本文給出了非等精度測量時電阻率的不確定度評定方法；探討了加權平均法和直線擬合法的A類不確定度和B類不確定的處理。并對等精度和非等精度測量結果的不確定度進行了對比分析。本文對非等精度的不確定度評定方法，可以為多個待測量中存在兩個線性變量而其它待測量真值不變情況下的不確定度處理提供參考。

2 等精度測量及不確定度評定

本實驗的電阻率采用間接測量，選用足夠長的直徑均勻的圓柱形低值電阻，分別測量電阻阻值、電阻直徑D和長度L，通過電阻率公式

計算電阻率。等精度測量時，固定長度L真值不變，在相同條件下重復測量各物理量6次。為了與后面不等精度數據的不確定度對比，我們分別測量了L分別約為419.8mm、399.9mm、380.0mm、360.0mm、340.0mm和320.0mm的數據，每個L等精度測量六組（篇幅所限，測量原始數據未列出）。

等精度測量結果的不確定度，根據誤差傳遞公式：

，先分別計算L、D和Rx的不確定度u（x），（其中，x=L、D、Rx），再由誤差傳遞公式求出電阻率的不確定度u（ρ）。其步驟如下：

（1）計算x（x=L、D、Rx）的A類不確定度。A類不確定度是用統計學方法計算的分量，是隨機誤差性質的不確定度。可視為實驗的標準偏差：

。

（2）計算x（x=L、D、Rx）的B類不確定度。B類不確定度，不滿足統計規律的分量，是系統誤差性質的不確定度。通常考慮儀器誤差引起的不確定度：

，其中△mL=0.1mm，

△mD=0.004mm，。

（3）計算x（x=L、D、Rx）的合成不確定度：

。

（4）計算x（x=L、D、Rx）的相對不確定度：

。

（5）計算電阻率ρ的不確定度：

；

為了與后面不等精度數據的不確定度對比，對于每個L處等精度測量的六組數據，我們都計算了其不確定度，結果列于表1。根據我國制定的不確定度實施指南，且為體現其差異性，表示不確定度時取兩位有效數字。由表中可以看出，隨著L的增大，不論是實驗的標準偏差還是相對不確定度都逐漸減小。因此，對于等精度測量，為了減小誤差，應選擇較大的L進行測量。

3 非等精度測量數據的加權平均法處理

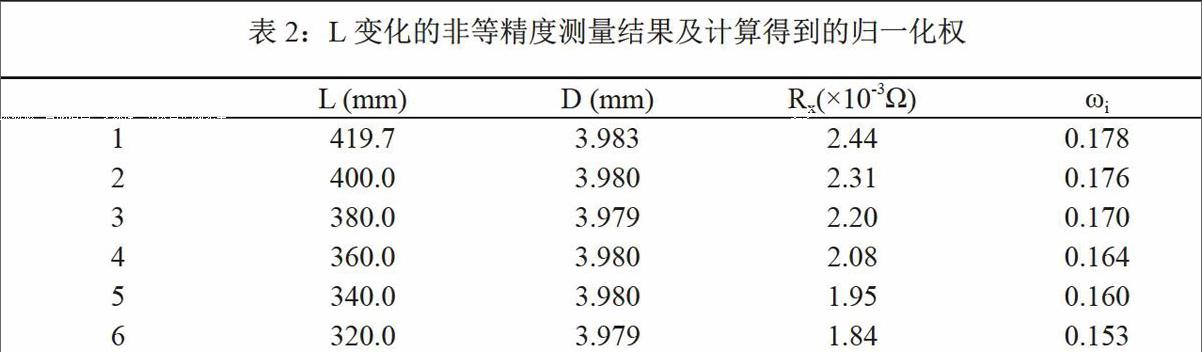
相比于L固定的等精度測量，實驗中還可采用改變L的非等精度測量電阻率的方案，采用這種方案，實驗過程具有變化性，操作不顯枯燥，更容易引起學生的興趣。表2給出了L等間距變化測量的六組數據。對其數據的處理有加權平均法和直線擬合法兩種方式，兩種數據處理不確定度的方法有一定的差異。此部分給出了加權平均處理A類和B類不確定度的方法。

3.1 最佳值ρO

從第二部分等精度測量結果的不確定度變化趨勢可知，L越小，測量結果的誤差越大，因此，ρ的最佳值不能直接平均求得，而應考慮單次測量的可靠程度。即最佳值ρ0表示為加權平均值：ρ0=∑iωiρi，其中ρi為第i次單次測量計算結果，ωi為其對應的歸一化權。ωi與單次測量的不確定度u（ρi）的關系為：

。計算u（ρi）時，因為其為單次測量的不確定度，因此不計入A類評定而只考慮B類評定為：

，其中，△mL=0.1mm，△mD=0.004mm，

。

計算得ρ0=7.19×10-5Ω·mm，略大于其平均值=7.18×10-5Ω·mm。由表2列出的權值ωi的計算結果可見，隨著 L增大，權值逐漸增加，這符合本實驗儀器的誤差變化規律。

3.2 A類不確定度

類似等精度測量的A類不確定度，但需計入加權平均。通常將加權平均的標準偏差記為其A類不確定度：

。計算結果為：uA（ρ）=0.016×10-5Ω·mm。

3.3 B類不確定度

大部分參考書和文獻[1-4]的非等精度測量不確定度評定只考慮了A類不確定度，但本實驗中，上述計算結果顯示，若只考慮A類評定，其結果與等精度測量的處理結果有很大差異。由于B類不確定度是系統誤差性質的不確定度，且考慮其權重，參考李震春等老師在伏安法測表頭內阻實驗中所采用的處理方法，我們將單次測量的不確定度u（ρi）的加權平均作為B類不確定度：uB（ρ）=∑iωiu（ρi）。計算結果為：uB（ρ）=0.610×10-5Ω·mm

3.4 合成不確定度

將A類和B類不確定度按其方和根法計算得：

u（ρ）=

=0.61×10-5Ω·mm；

其最終結果為：ρ=（7.19±0.61）×10-5Ω·mm（P=68.3%），E（ρ）=8.5%。

4 非等精度測量數據的直線擬合法處理

本實驗中，測量電阻阻值Rx、電阻直徑D和長度L三者之間雖然不具備線性關系，但根據電阻率公式以及表2非等精度的測量結果看，電阻阻值Rx與電阻長度L存在線性關系。我們引入一個中間量k，定義為：

，則電阻率表示為。根據k和直徑D的特點，我們提出，ρ的最佳值根據公式

確定，而其不確定度根據誤差傳遞公式來計算。

4.1 直徑D的不確定度評定

直徑D的不確定度評定采用與第二部分中等精度測量的相同處理方法，計算得到：

=3.9802mm；u（D）==0.0024mm；E（D）=0.060%。

4.2 中間量k的最佳值和不確定度評定

根據Rx=kL，（Rxi，Li）的測量值可用過原點的直線來擬合，其斜率k的最佳值可表示為：k=（∑iLiRxi）/∑iL2i。計算結果為：k=5.78×10-3Ω/mm。

k的A類不確定度一般為擬合直線中斜率k的標準偏差：

。計算得到uA（k）=0.011×10-3Ω/mm。顯然，k的A類不確定度較小，若只考慮A類不確定度，其最終結果仍與前面計算結果有很大差異。因此，我們進一步計算了k的B類不確定度。

由于B類不確定度是系統誤差性質的不確定度，考慮本部分為直線Rx=kL擬合結果，我們將直線中處的單次測量不確定度作為k的B類不確定度，其實質為直線上該處的儀器誤差，即：

，

其中。計算得：uB（k）=0.489×10-3Ω/mm。

綜上，可以得到中間量k的最佳值和不確定度分別為：k=5.78×10-3Ω/mm；u（k）==0.49×10-3Ω/mm；E（k）=8.5%

4.3 ρ的直線擬合法數據不確定度處理結果

將D和k的不確定度按誤差傳遞公式計算得：

u（ρ） =

=0.61×10-5Ω·mm；

E（ρ）==8.5%。

5 三種方法不確定度比較分析

根據以上結果可知：

（1）比較等精度測量的不確定度結果發現，L真值較大時，實驗誤差更小。

（2）非等精度測量的不確定度評定時：若不計入B類不確定度，結果與等精度處理結果有很大差異；采用本文的方法計入B類不確定度，其結果與介于L=380cm到L=360cm的等精度處理結果非常接近。由此可見，非等精度不確定度評定時，若不計算B類不確定度是不合理的，在處理非等精度不確定度時，仍應該考慮B類不確定度。

（3）兩種非等精度數據處理方法得到的結果一致。本實驗中所采用的加權平均法與大部分實驗所使用的加權平均法相同，且與等精度測量的不確定度相近，其結果的準確性能夠得到認可。而本實驗中所改進的直線擬合法處理的結果與加權平均法一致，可見我們提出的對具有兩個線性變量而其它待測量真值不變的多待測量實驗的不確定度評定方法是合理可行的。

6 結論

本文討論了直流雙臂電橋測低值電阻電阻率實驗中，等/非等精度測量不確定度評定的方法與步驟，結果的分析對比發現，等精度測量時，為減小誤差，應盡可能的選擇較大的L進行測量；非等精度測量時，B類不確定度對結果具有很大影響不可忽略。本文對非等精度測量中不確定度的直線擬合處理法進行了改進，提出了針對具有兩個線性變量而其它待測量真值不變的多待測量實驗的不確定度的直線擬合法。從數據的處理結果來看，該方法合理可行，對具有類似特征的多待測量實驗具有較大的參考價值。

參考文獻

[1]訾振發，趙敏，章韋芳.不確定度理論在重力加速度測量實驗中的應用[J].合肥師范學院學報，2013，31（06）：63-65.

[2]原媛，沈元華，趙在忠，金浩明，馬秀芳，孫燕青，馬世紅.惠斯通電橋實驗中對互易橋臂測量結果的不確定度評定[J].物理實驗，2014，34（07）：33-36.

[3]徐紅，曹冬梅.非等精度測量電阻的數據處理[J].價值工程，2012，03：0262-0263.

[4]張德根.單擺實驗中不等精度測量的不確定度分析[J].大學物理實驗，2013，26（06）：0092-0094.

[5]李震春，左衛群，曾衛東.非等精度測量方案數據處理方法的探討[J].廣西物理，2007，28（04）：44-47.