Narendra自適應控制器在球桿系統的應用與研究

高 成,郝洋洋

(沈陽工業大學化工過程自動化學院,遼寧 遼陽 111003)

Narendra自適應控制器在球桿系統的應用與研究

高 成,郝洋洋

(沈陽工業大學化工過程自動化學院,遼寧 遼陽 111003)

作為經典的試驗設備之一，球桿系統具有開環不穩定和非線性這兩大特性，是控制理論研究的典型對象，是自動控制試驗室常用裝置，是試驗人員實踐控制理論基礎的平臺，也是驗證設計人員的新想法、新思路的典型設備。建立了球桿系統及其數學模型，對某些環節進行了線性化處理，得到整個球桿系統的簡化模型，作為被控對象的傳遞函數。基于球桿系統傳遞函數的特點，設計了一種Narendra自適應控制器，并在Matlab中的Simulink環境下進行實時控制，以驗證控制器的控制效果。仿真和試驗結果都表明，與PID控制、根軌跡控制相比，自適應控制具有更好的控制效果。自適應控制理論為解決復雜系統控制問題開辟了新的途徑，已成為控制領域的研究和發展熱點。

控制理論； 自適應控制器； 濾波器； 伺服電機； 電機傳動

0 引言

在控制理論的研究中，球桿系統是最為著名的試驗設備之一，許多專家、學者都通過球桿系統對其研究的理論進行驗證。因球桿系統是一個經典的非線性、單輸入單輸出、開環不穩定系統，且小球在導軌上的運動十分復雜，故球桿系統得到了廣泛的應用。

球桿系統的基本控制思路是：通過控制直流伺服電動機的正反轉，帶動傳動機構調節橫桿的傾斜角度，實現對小球運動的控制，進而達到預期位置[1]。本文采用牛頓-歐拉公式建立球桿系統的數學模型,并根據該數學模型選擇合適的控制器。

1 系統建模

球桿系統是典型的非線性系統，其運動機構具有許多非線性特點，包括：飽和、死區特性，直流伺服電動機、帶輪和連動桿傳動的非線性，小球運動軌跡的非線性，小球運動過程中受到空氣及非絕對光滑的導軌產生的非線性阻力。 因此，對小球在導軌表面運動動態過程的完整描述是十分復雜的，建模的目的是對該控制系統給出一個較為簡單的模型[2-3]。球桿系統機械結構如圖1所示。

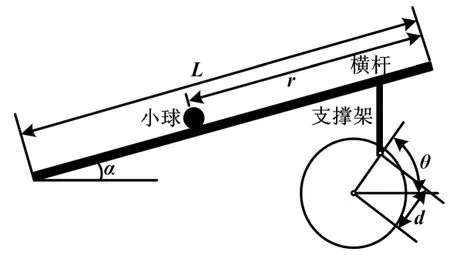
圖1 球桿系統機械結構示意圖

電機帶動帶輪轉動，連接線(皮帶輪中心到支撐架與皮帶輪連接點的連接線)和水平線的夾角角度為θ(θ有相應的限定范圍)；連桿隨之帶動橫桿轉動，角度為α；橫桿轉動過程中，小球因重力作用開始在橫桿內滾動[4]。

皮帶輪中心到支撐架與皮帶輪連接點的距離為d，橫桿的長度值為L，由此可得出傾斜角α與θ之間的近似數學關系式為：

(1)

式中：d為齒輪半徑，d=45 mm；L為支撐桿橫桿連接點的長度,L=400 mm[5]。

電動機傳動軸和θ之間存在一個同步帶(減速比n=4)，控制器的設計目的是通過整定θ，保證小球在特定位置保持平衡。

通過運動學對小球的運動情況進行分析，其慣量、重力、轉角、位移之間的關系為[6-7]：

(2)

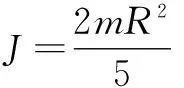
假設小球在橫桿上的運動為滾動，且摩擦力可以忽略不計，α很小，則：

sinα=α

(3)

(4)

將式(2)～式(4)化簡,得：

(5)

將式(1)代入式(5)，可得：

式中：r為系統輸出量，是小球在平衡桿上的位置；θ為輸入量，是轉盤的轉角。

當以θ為系統輸入量時，r和θ的傳遞函數為：

2 Narendra自適應控制器的設計

被控對象的狀態、輸出方程分別為：

(6)

yp=hTxp

(7)

式中：Ap、bp為未知量；xp為n維狀態向量；yp為輸出量；u為控制量；h為n×1維向量。

因此，被控系統的傳遞函數為：

Gp(s)=hT(sI-Ap)-1bp=kpNp(s)/Dp(s)

(8)

式中：kp為被控對象增益。

選取參考模型為：

xm=Amxm+bmyr

(9)

ym=hTxm

(10)

式中：yr為輸入信號；ym為輸出信號。

參考模型傳遞函數為：

Gm(s)=hT(sI-Am)-1bm=kmNm(s)/Dm(s)

(11)

式中：km為參考模型增益。

設廣義輸出誤差函數為：

e(t)=ym(t)-yp(t)

根據李雅普諾夫穩定性理論[8]設計自適應控制律(不含誤差倒數)，使廣義輸出誤差函數滿足以下條件：

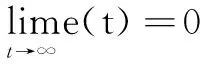
(12)

當式(12)成立時，控制系統具備良好的跟蹤性能，達到了設計要求。

當自適應控制器中的可調參數足夠多時，可以實現參考模型與可調系統的完全匹配。當控制對象傳遞函數中的分子為m階、分母為n階、被控對象增益為kp時，可調參數數量可多達(n+m+1)個，因此與之對應的自適應機構也應為(n+m+1)個。

因此，自適應控制器可設計如下。

①選擇L(s)=s+a(a>0)，使得L(s)G(s)為嚴格正實函數。

②選擇Df(s)=L(s)Nm(s)，并構造輔助信號狀態方程:

③可調參數自適應律為：

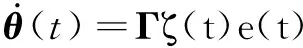
(13)

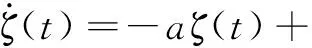
(14)

式中：θT=[k0c d0d]；φT=[yrv1ypv2]；e(t)=ym(t)-yp(t)；Γ為正定對稱矩陣。

④設計非線性自適應控制律為：

u(t)=θT(t)φ(t)+e(t)ζT(t)Γζ(t)

3 Narendra自適應控制器的實現

通過分析Narendra模型參考自適應控制理論，依據參考模型傳遞函數，并選用穩定多項式L(s)=s+a，可證明函數L(s)Gm(s)為嚴格正實函數。

定義增廣狀態向量為:

(15)

由式(15)可知：ζ1=yr/(s+a)；ζ2=v1/(s+a)；ζ3=yp/(s+a)；ζ4=v2/(s+a)。

為使得被控系統的輸出信號與參考模型一致，設計可調參數向量θ為：

θT=[k0cd0d]

選擇信號濾波器：

Df(s)=L(s)Nm(s)=(s+a)×(s+1)

(16)

由式(16)獲得濾波信號：

v1=u/(s+a)

v2=yp/(s+a)

選擇自適應控制律：

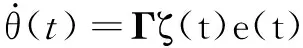
(17)

由式(17)可得：

根據式(17)和式(15)，得到控制律為[9]：

4 仿真設計

被控對象的數學模型為：

Gp(s)=1.853/s2

(18)

根據被控對象選擇的參考模型為：

(19)

構建的Narendra模型參考自適應控制系統模型如圖2所示。在圖2中，輸入系統的數學模型、參考模型，并進行仿真操作。

圖2 Narendra自適應控制系統模型示意圖

①在階躍信號的作用下，PID控制的動態響應曲線如圖3所示。根據圖3分析可知，PID存在較大的超調量，調節時間較長，并且在一段時間之后出現震動，系統趨于穩定，控制性能良好。

②在階躍信號作用下，根軌跡控制的動態響應曲線如圖4所示。根據圖4分析可知，根軌跡控制存在較大的超調量，調節時間較長，穩定后存在穩態誤差，控制性能一般。

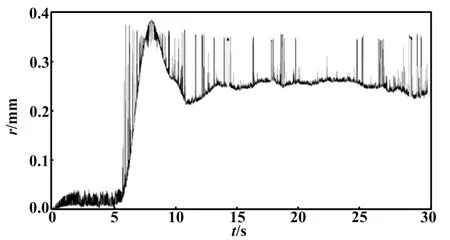
圖4 根軌跡控制的動態響應曲線

③在階躍信號作用下，自適應控制的動態響應曲線如圖5所示。根據圖5分析可知，自適應控制具有非常好的控制性能。根據參考模型的變化，控制器可以較快地跟隨參考模型進行變化。其超調量較小，調節時間較短，控制效果優于PID控制和根軌跡控制。

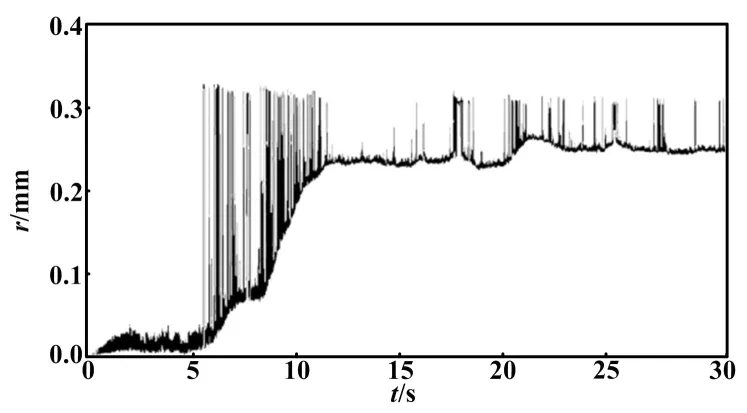
圖5 自適應控制的動態響應曲線

5 結束語

對自適應控制方法在球桿系統上的應用進行研究，建立球桿系統的數學模型，選擇Narendra控制器。在Simulink中，選擇多種控制算法,包括PID控制[10-11]、根軌跡控制和自適應控制[12-13]，對球桿系統進行實時控制。由實時控制的結果分析可知，在采用了Narendra自適應控制器后，球桿系統達到了較好的控制效果。在輸入信號變化的過程中，控制系統都可以保持良好的跟蹤性能。

[1] 彭秀艷,宮彬.球桿系統的控制方法研究[J].應用科技,2009,32(12):37-40.

[2] 劉陽,萬隆君,徐軼群.淺談球桿系統的建模與仿真[J].中國科技信息,2014 (6);159-161.

[3] 吳偏偏,王富東,王敬馳.球桿控制系統的設計[J].行業應用與交流,2015,34(9):114-116.

[4] 宋志偉,翟文鵬,信建峰,等.基于PID算法的球桿教學系統設計[J].硅谷,2015 (3):5-6.

[5] 李志民,柳強,張新權,等.基于最小二乘法的球桿系統輸入輸出建模研究[J].研究與開發,2016,35(1):65-69.

[6] 鄭艷偉,張井崗.球桿系統的滑模變結構控制[J].太原科技大學學報,2014,35(2):97-101.

[7] 樓旭陽.基于球桿系統的現代控制理論課堂教學實例設計[J].高教學刊,2016 (8):78-80.

[8] 白珍龍,劉川來.應用Lyapunov理論設計分數階模型參考自適應控制律[J].石油化工自動化,2015,51(5):44-47.

[9] 龐中華,崔紅.系統辨識與自適應控制MATLAB仿真[M].北京:北京航空航天大學出版社,2009:82-83,87.

[10]俞同云.基于閉環特征參數的球桿系統自適應PID控制策略[D].長沙:中南大學,2013.

[11]KRISHNA B,GANGOPADHYAY S,GEORGE J.Design and simulation of gain scheduling PID controller for ball and beam system[D].Signal Processing and Electronics Engineering,2012:199-203.

[12]李寧,袁惠群,孫海義,等.Adaptive control of bifurcation and chaos in a time-delayed system[J].Chinese Physics B,2013,22(3)：030508.

[13]劉幸,劉瀟.自適應控制系統的發展與應用[J].學術研究,2011:61-63.

Research on the Application of Narendra Adaptive Controller in Ball-Beam System

GAO Cheng,HAO Yangyang

(College of Chemical Process Automation，Shenyang University of Technology,Liaoyang 111003,China)

As one of the classic experimental equipment,the ball-beam system features open loop instability and nonlinearity,and it is a typical object in research of control theory.It is the commonly used device in automatic control laboratory,and the platform for testers practicing theoretical basis,also it is the typical device for designers verifying their new concept and new ideas.The ball-beam system and its mathematic model are established,and some of the sections are processed for linearity,thus the simplified model of the whole ball-beam system is obtained,and used as the transform function of the controlled object.In accordance with the features of the transfer function of ball-beam system,the Narendra adaptive controller is designed,and the control effects of the controller are verified by conducting real time control in Matlab/Simulink environment.The results of simulation and tests all indicate that,comparing with PID control and root locus control,the adaptive control has excellent control effects.The generation of the adaptive control theory has opened up a new way for solving the problem of complex system control,and become the hotspot in the fields of research and development.

Control theory; Adaptive controller; Filter; Servo motor; Motor drive

遼寧省自然科學基金資助項目(2015020103)

高成(1970—)，男，博士，副教授,主要從事智能控制、機器人方向的研究。E-mail:gc_7011@163.com。

TH7;TP273+.2

A

10.16086/j.cnki.issn1000-0380.201704005

修改稿收到日期：2017-01-17