恒流源負載V2控制Buck變換器的穩定性分析

吳志敏,楊 艷,史國棟,包伯成,姚凱文

(常州大學信息科學與工程學院,江蘇 常州 213164)

恒流源負載V2控制Buck變換器的穩定性分析

吳志敏,楊 艷,史國棟,包伯成,姚凱文

(常州大學信息科學與工程學院,江蘇 常州 213164)

恒流源負載開關變換器在發光二極管照明領域具有廣闊的應用前景，其研究具有理論意義和應用價值。為了研究電路參數對恒流源負載V2控制Buck變換器穩定性的影響，建立了該變換器的二階離散迭代映射模型，得到了輸出電容等效串聯電阻、恒流源負載變化時的分岔圖。分析結果表明，當輸出電容等效串聯電阻、恒流源負載變化時，恒流源負載V2控制Buck變換器具有復雜的動力學行為。利用特征值和最大李雅普諾夫指數對系統進行穩定性分析，驗證了分岔分析的正確性。通過數值仿真得到了輸出電容及其等效串聯電阻之間的工作狀態邊界，揭示了輸出電容時間常數穩定臨界值與開關周期間的非線性關系。最后，基于PSIM電路仿真和電路試驗，得到了輸出電容等效串聯電阻時的時域波形，驗證了二階離散迭代映射模型的有效性和理論分析的正確性。

電力電子； 二極管；恒流源負載; Buck變換器; 輸出電容;穩定性分析

0 引言

發光二極管(light emitting diode,LED)照明是通過控制LED負載實現恒流照明[1]，在實際開關變換器中，LED負載可等效為恒流源負載，故恒流源負載開關變換器是今后電力電子的重要研究和應用方向。V2控制因其快速的動態響應而得到廣泛關注[2]，因此，對恒流源負載V2控制Buck變換器進行深入研究具有重大的理論意義和應用價值。

開關變換器存在低頻波動、次諧波振蕩、倍周期分岔、邊界碰撞分岔和不穩定混沌振蕩等非線性動力學現象[3-6]。不穩定混沌振蕩的出現會極大地影響開關變換器的控制性能，甚至導致開關變換器無法正常工作。因此，有必要運用動力學方法對開關變換器中存在的一系列非線性動力學現象進行研究，同時深入分析電路參數的變化對變換器穩定性的影響，以指導開關變換器的參數設計。

本文根據恒流源負載V2控制Buck變換器的狀態方程，建立其二階離散迭代映射模型。根據此模型研究了輸出電容等效串聯電阻(equivalent series resistance,ESR)R0和恒流源負載Io的變化對開關變換器的穩定性影響，分析了開關變換器存在的周期振蕩、倍周期分岔、次諧波振蕩、不穩定的混沌振蕩等復雜物理現象[3-6]。電路參數范圍和穩定性邊界[7-9]對于變換器的電路設計和參數選擇具有重要的指導意義。本文通過對輸出電容ESR R0和輸出電容C的仿真研究，得到了在R0-C平面上的工作狀態區域分布圖，并采用電力電子仿真軟件(power simulation,PSIM)進行電路仿真和電路試驗，以驗證理論分析結果。

1 恒流源負載V2控制Buck變換器

1.1 工作原理

恒流源負載V2控制Buck變換器的電路原理圖如圖1所示。

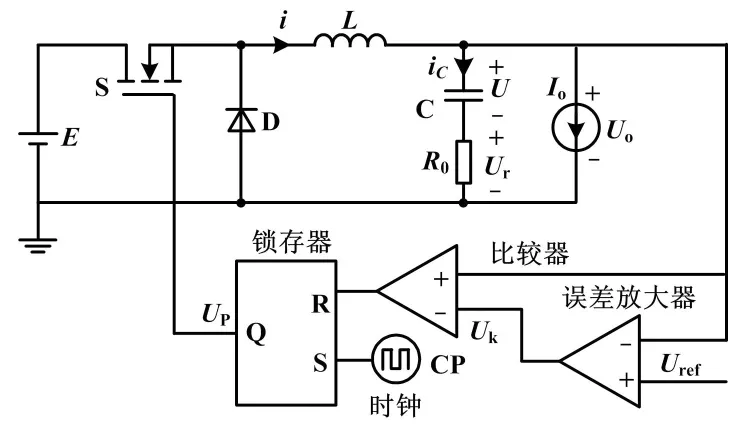
圖1 恒流源負載V2控制Buck變換器原理圖

恒流源負載V2控制Buck變換器的功率級主電路由輸入電壓E、輸出電容C及其ESR R0、開關管S、二極管D、恒流源負載Io和儲能電感L組成[2]；恒控制電路由誤差放大器、比較器、RS鎖存器、時鐘脈沖CP等組成。開關周期開始時，RS輸出高電平，S導通，D關斷，Uo增大。當Uo增大到Uk時，S關斷至下一個開關周期開始[2,6]。由圖1可知，當開關狀態發生切換時，輸出電壓Uo滿足：

Uo=Uk=K(Uref-Uo)

(1)

式中：Uref為參考電壓；K為誤差放大器的比例系數。

由式(1)可得，開關狀態發生切換時的Uo為：

(2)

1.2 狀態方程

根據開關管S和二極管D的開關狀態，Buck變換器有3種工作模式：①S導通、D截止；②S關斷、D導通；③S關斷、D截止。在斷續導電模式(discontinuous conduction mode,DCM)下，3種工作模式均存在；而在連續導電模式(continuous conduction mode,CCM)下，僅存在工作模式①和②。

設t=t0=nT為變換器在DCM模式下第n個開關周期內的初始時刻；t=t1為S從導通至關斷、D從關斷至導通的切換時刻；t=t2為D從導通至關斷的切換時刻；t=t3=(n+1)T為該開關周期的終止時刻。τ1=t1-t0、τ2=t2-t1和τ3=t3-t2分別為3種不同開關狀態內的持續時間。

則恒流源負載V2控制Buck變換器在第n個開關周期內的狀態方程為：

(3)

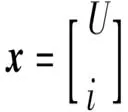
1.3 二階離散映射模型

狀態變量在t=t0=nT時刻的采樣值為該開關周期的初值，可表示為xn=[Un,in]T；在t=(n+1)T時刻的采樣值為該開關周期的終值，即下個開關周期的初值，可表示為xn+1=[Un+1,in+1]T。

首先，變換器進入工作模式①。根據式(3)的第一個方程，可得變換器經過時間間隔τ1后，在t=t1時刻的電容電壓和電感電流分別為：U1(t1)=e-ατ1[(Un-E)cos(ωτ1)+k1sin(ωτ1)]+E

(4)

i1(t1)=e-ατ1[(in-Io)cos(ωτ1)+k2sin(ωτ1)]+Io

(5)

隨后，變換器進入工作模式②。根據式(3)的第二個方程，以式(4)、式(5)的結果為初值，可得變換器經過時間間隔τ2后,在t=t2時刻的電容電壓和電感電流分別為：

U2(t2)=e-αt2[U1(t1)cos(ωτ2)+k3sin(ωτ2)]

(6)

i2(t2)=e-αt2{[i1(t1)-Io]cos(ωτ2)+k4sin(ωτ2)}+Io

(7)

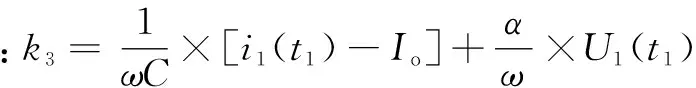
最后，變換器進入工作模式③。根據式(3)的第3個方程，以式(6)、式(7)的結果為初值，可得變換器經過時間間隔τ3后，在t=t3時刻的電容電壓和電感電流分別為：

(8)

i3(t3)=0

(9)

由V2控制Buck變換器的原理可知，當Uo(t1)=Uk時，開關管由導通切換為關斷，故工作模式①至

工作模式②的切換條件為：

U1(t1)+R0i1(t1)-R0I0=Uk

(10)

由式(10)可借助數值計算方法求出τ1。當變換器工作于CCM時，τ2=T-τ1、τ3=0；而當變換器工作于DCM時，令式(7)中的i2(t2)=0，可求出τ2，則τ3=T-τ2-τ1。得到τ1和τ2后，根據式(4)～式(9),可分別得到τ1≥T、τ1+τ2>T、τ1+τ2≤T這3種情況下的二階離散迭代映射模型。

當τ1≥T時，在第n個開關周期內，變換器始終運行在工作模式①，則此時二階離散迭代映射模型為：

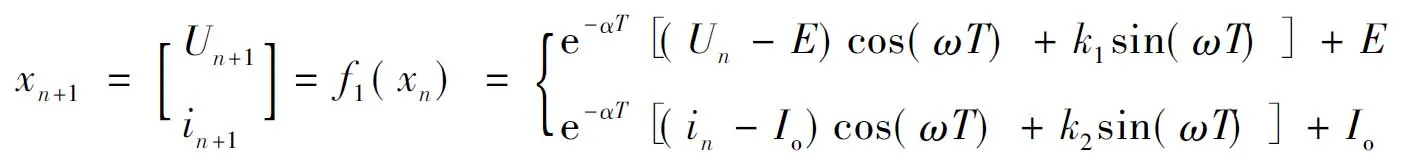
(11)

當τ1+τ2>T時，變換器于CCM工作，此時二階離散迭代映射模型為：

(12)

當τ2+τ2≤T時，變換器于DCM工作，此時二階離散迭代映射模型為：

(13)

式(11)～式(13)構成了V2控制Buck變換器的二階離散迭代映射模型。

定義變換器的輸出電壓邊界Ub為在時鐘周期開始時的輸出電壓值，在時鐘周期結束時輸出電壓剛好到達控制電壓Uk。結合式(4)和式(5)，可得邊界值Ub為：

(14)

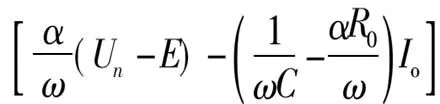
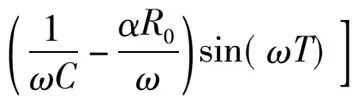
2 動力學行為分析

2.1 分岔分析

根據式(11)～式(13)的二階離散迭代映射模型，選擇表1所示電路參數，以輸出電容ESR和恒流源負載為分岔參數，得到的數值仿真分岔圖如圖2所示。

表1 電路參數

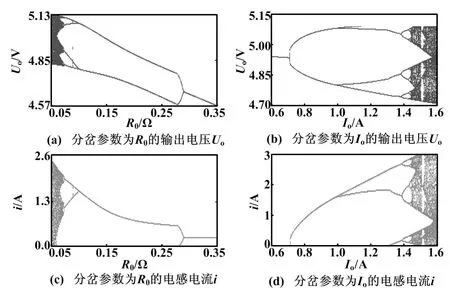
圖2 數值仿真分岔圖

圖2(a)和圖2(c)中，Io=1 A，R0=0.05～0.35 Ω。

當R0>0.284 Ω時，變換器工作在穩定的CCM周期振蕩狀態；隨著R0的減小，在R0= 0.284 Ω處，變換器經倍周期分岔[10]進入到CCM次諧波振蕩狀態；在R0=0.27 Ω處，變換器發生工作模式轉移，從CCM次諧波振蕩狀態進入DCM次諧波振蕩狀態；隨著R0的繼續減小，在R0=0.103 Ω和R0=0.085 Ω處，變換器的運行軌道與邊界發生碰撞而引發邊界碰撞分岔；在R0=0.072 Ω處運行軌道經邊界碰撞分岔進入DCM混沌振蕩狀態。由分岔分析可知，通過增大R0，可使恒流源負載V2控制Buck變換器工作在穩定的CCM周期振蕩狀態。

圖2(b)和圖2(d)中:R0=0.1 Ω，Io=0.6～1.6 A。當Io<0.72 A時，變換器工作在穩定的DCM周期振蕩狀態；隨著Io的增大，在Io=0.72 A處，變換器經倍周期分岔進入到DCM次諧波振蕩狀態；隨著Io的繼續增大，在Io=1.094 A和Io=1.388 A處，變換器分別發生了邊界碰撞分岔和第二次倍周期分岔；在Io=1.43 A處，運行軌道經邊界碰撞分岔進入DCM混沌振蕩狀態[10-12]。由分岔分析可知，通過減小恒流源負載Io，可使恒流源負載V2控制Buck變換器工作在穩定的DCM周期振蕩狀態。

2.2 穩定性分析

對離散迭代映射模型不動點處的雅克比矩陣及其特征根進行分析，可確定開關變換器穩態工作時的穩定性[2]。令xn+1=xn=XQ，恒流源負載V2控制Buck變換器的離散迭代模型在不動點XQ處的雅克比矩陣為：

(15)

式中：J11=?Un+1/?Un;J12=?Un+1/?in;J21=?in+1/?Un;J22=?in+1/?in。

以τ1≥T時為例，在第n個開關周期內，變換器始終運行在工作模式①，則矩陣系數Jij(i，j=1,2)分別為:

J11=e-αT[cos(ωT)+αsin(ωT)/ω]

(16)

J12=e-αTsin(ωT)/ωC

(17)

J21=-e-αTsin(ωT)/ωL

(18)

J22=e-αT[cos(ωT)-αsin(ωT)/ω]

(19)

根據所得雅克比矩陣，可得相應的特征方程為：

det [λI-Jn(XQ)]=0

(20)

由式(16)得到的2個特征值λ1和λ2的變化，可判定恒流源負載V2控制Buck變換器的穩定運行參數區間。

表2給出了Io=1 A，R0=0.28～0.29 Ω時的特征值。從表2可以看出，隨著R0逐漸增大，離散迭代映射模型的一個實數特征值從-1進入單位圓，存在倍周期分岔現象。特征值走向分析結果與分岔分析一致，驗證了分岔圖的正確性。

表2 隨R0變化的特征值

2.3 最大Lyapunov指數

Lyapunov指數是判斷非線性系統存在混沌行為與否的重要手段[2,10-12]。恒流源負載V2控制Buck變換器的最大Lyapunov指數可表示為：

(21)

根據式(17)可知，與圖2對應的最大Lyapunov指數譜如圖3所示。

圖3 最大Lyapunov指數譜

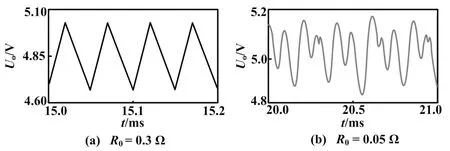
由圖3(a)可以看出，當R0>0.072 Ω時，λm>0，變換器處于混沌振蕩狀態；當R0=0.085 Ω時，λm從負數上升到零，對應圖2(a)中的第一次邊界碰撞分岔點；當R0=0.103 Ω時，λm從負數上升到零，對應圖2(a)中的第二次邊界碰撞分岔點；當0.103 Ω

由圖3(b)可看出，當Io<0.72 A時，變換器處于周期振蕩狀態；當Io= 0.72 A時，λm上升到零，對應圖2(b)中的倍周期分岔點；當0.72 A1.43 A時，變換器處于混沌振蕩狀態，且在Io>1.43 A區間有小部分范圍內λm<0，說明變換器存在周期窗。對比圖2與圖3，可以看出分岔分析結果與最大Lyapunov指數分析結果一致。

3 工作狀態分析

由分岔分析可知，在R0減小的過程中，存在工作模式轉移。通過Matlab與PSIM仿真，得到CCM下R0-C平面上的穩定與不穩定區域分布圖如圖4所示。

圖4 穩定與不穩定區域分布圖

R0-C平面上的工作狀態邊界值如表3所示。

表3 R0-C平面上工作狀態邊界值

由表3可知，恒流源負載V2控制Buck變換器中，R0的穩定CCM邊界值隨著輸出電容C的變化而不斷變化；R0×C的穩定邊界值與開關周期T呈現非線性關系，與電阻負載V2控制Buck變換器有著顯著區別。

4 電路仿真與試驗驗證

4.1 電路仿真

利用PSIM軟件，搭建恒流源負載V2控制Buck變換器的仿真電路，并對其進行PSIM仿真。采用表1參數，其他電路參數保持不變，以R0為例，得到不同參數下的輸出電壓Uo的時域波形圖如圖5所示。

圖5 PSIM仿真波形圖

由圖5(a)可知，當R0=0.3 Ω時，變換器工作在CCM周期振蕩狀態；由圖5(b)可看出，當R0=0.05 Ω時，變換器工作在DCM混沌振蕩狀態。PSIM仿真結果與分岔分析結果一致。

4.2 試驗驗證

為進一步驗證理論分析結果，以R0為例，選擇與PSIM仿真相同的參數，建立相應的試驗平臺進行驗證。誤差放大器選用LM358N，比較器采用LM319，RS觸發器采用芯片74ALS02，MOSFET開關管采用IRF3205N，選用IR2125芯片作為MOS管的驅動。為保證試驗的準確性，試驗操作時使用電子負載來替代恒流源負載和輸出電容ESR。此外，時鐘脈沖CP由雙蹤信號發生器提供。

保持其他電路參數不變，不同R0下輸出電壓紋波ΔUo時域波形圖如圖6所示。

從圖6可看出，當R0=0.3 Ω時，變換器工作于CCM周期振蕩狀態；當R0=0.05 Ω時，變換器工作于DCM混沌振蕩狀態。隨著R0的減小，變換器由CCM周期振蕩狀態轉變為DCM混沌振蕩狀態。試驗結果與PSIM仿真結果、分岔分析結果一致。

5 結束語

本文通過恒流源負載V2控制Buck變換器在3種工作模式下的狀態方程，導出了它的二階離散迭代映射模型，并基于該模型研究了輸出電容ESR和恒流源負載對變換器的動力學特性影響。分岔分析結果表明：隨著輸出電容ESR的逐漸減小或恒流源負載的增大，變換器將逐漸從穩定的CCM周期振蕩狀態經倍周期、邊界碰撞等分岔行為進入次諧波振蕩狀態，最終進入不穩定的混沌振蕩狀態。

通過特征值變化和最大李雅普諾夫指數研究了系統的穩定性。研究結果表明，輸出電容ESR越大，變換器的工作狀態越趨于穩定；輸出電容ESR越小，變換器越容易進入到DCM混沌振蕩狀態，結論與分岔分析一致。此外，本文研究了在R0-C平面上的工作狀態區域分布。PSIM仿真和電路試驗很好地驗證了理論分析的正確性。

[1] 周國華,許建平,包伯成,等.電流源負載電流控制Buck變換器的復雜次諧波振蕩現象[J].物理學報,2011,60 (1):51-58.

[2] 何圣仲,周國華,許建平,等.輸出電容時間常數對V2控制Buck變換器的動力學特性的影響[J].物理學報,2014,63 (13):25-36.

[3] 張希,許建平,包伯成，等.固定關斷時間控制Buck變換器斜坡補償技術及其機理研究[J].中國電機工程學報,2014,

34(36):6426-6434.

[4] 馬正華,王國云,包伯成,等.脈沖序列控制反激式變換器邊界碰撞分岔與電路參數估計[J].電工技術學報,2013,28(12):262-268.

[5] 包伯成,楊平,馬正華,等.電路參數寬范圍變化時電流控制開關變換器的動力學研究[J].物理學報,2012,61(22):220502.

[6] 史國棟,楊艷,張希,等.電感與負載對V2控制Buck 變換器的動力學影響[J].自動化儀表,2016,37(4):12-15.

[7] ZHOU G H,HE S Z,ZHANG X,et al.Critical output-capacitor ESR for the stability of V2 controlled buck converter in CCM and DCM [J].Electronics Letters,2014,50(12):884-886.

[8] BAO B C,ZHANG X,XU J P,et al.Critical Esr of output capacitor for stability of fixed off-time controlled buck converter[J].Electronics Letters,2013,49(4):287-288.

[9] BAO B C,YANG J,XU J P,et al.Effect of output capacitor ESR on dynamic performance of voltage-mode hysteretic controlled buck converter[J].Electronics Letters,2013,49(20):1293-1294.

[10]XIE F,YANG R,ZHANG B.Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns[J].IEEE Transactions Circuits and Systems I:Regular Papers,2011,58(9):2269-2280.

[11]BAO B C,ZHOU G H,XU J P,et al.Unified classification of operation-state regions for switching converters with ramp compensation[J].IEEE Transactions Power Electronics,2011,26(7):1968-1975.

[12]ZHANG X,XU J P,BAO B C,et al.Asynchronous-switching map-based stability effects of circuit parameters in fixed off-time controlled buck converter[J].IEEE Transactions Power Electronics,2016,31(9):6686-6697.

Stability Analysis of V2Controlled Buck Converter with Constant Current Source Load

WU Zhimin,YANG Yan,SHI Guodong,BAO Bocheng,YAO Kaiwen

(School of Information Science and Engineering,Changzhou University,Changzhou 213164,China)

Switching converter with constant current source load has a wide application prospect in the lighting field of emitting diode,and therefore the study of V2controlled buck converter with constant current source load has theoretical significance and application value.In order to investigate the influence of circuit parameters on stability of V2controlled buck converter with constant current source load,a second order discrete iterative mapping model is established，based on which the bifurcation diagrams with the variations of the equivalent series resistance of output capacitor and constant current source load are obtained.The results show that the converter has complex dynamic behavior when the equivalent series resistance of output capacitor and constant current source load change.Stability of the system is analyzed by using the eigenvalues and maximum Lyapunov exponent,which validates the correctness of bifurcation analysis.The operation state boundaries between the output capacitor and its equivalent series resistance are obtained by numerical simulations,and the nonlinear relationship between the stable critical value of output capacitor time constant and the switching cycle is revealed.Based on PSIM circuit simulations and circuit experiments,the time domain waveforms under different equivalent series resistance of output capacitor are received.Thus,the effectiveness of the second order discrete iterative mapping model and the correctness of theoretical analysis are verified.

Power electronics; Diode; Constant current source load; Buck converter; Output capacitor; Stability analysis

常州市自然科學基金資助項目(CJ20159026)

吳志敏(1977—)，女，碩士，講師，主要從事電能變換與控制技術的研究。E-mail:wuzhimin@cczu.edu.cn。 楊艷(通信作者)，女，在讀碩士研究生，主要從事電能變換與控制技術的研究。E-mail:yangyan_Tiffany@163.com。

TH82;TP391

A

10.16086/j.cnki.issn1000-0380.201704017

修改稿收到日期：2017-01-16