大視場星敏感器光學系統畸變校正方法

李建華，李志峰，牛振紅，趙 茜，劉佳琪,2

（1. 試驗物理與計算數學國家重點實驗室，北京，100076；2. 北京航天長征飛行器研究所，北京，100076）

大視場星敏感器光學系統畸變校正方法

李建華1，李志峰1，牛振紅1，趙 茜1，劉佳琪1,2

（1. 試驗物理與計算數學國家重點實驗室，北京，100076；2. 北京航天長征飛行器研究所，北京，100076）

針對大視場星敏感器光學系統畸變較大，嚴重影響角距測量精度的問題，采用多項式擬合算法，對研制的星敏感器進行了畸變校正，校正后的平均角度測量誤差小于1″。

星敏感器；畸變校正；多項式擬合

0 引 言

利用星敏感器修正慣性導航系統的漂移累積誤差是實現航天器自主姿態測量的首選途徑。星敏感器以太空中的恒星作為姿態測量的參考源，通過星圖識別，輸出其在慣性參考系中的指向，是目前航天器測量精度最高的一種定姿設備[1]，在民用和軍用領域得到了廣泛的應用[2]。

大視場星敏感器是指視場在20°左右的星敏感器[3,4]，由于視場較大，單幅星圖的星點數較多，星圖匹配正確率高，因此得到廣泛使用。但同時由于視場較大，光學系統畸變引起的測量誤差也很大，難以滿足高精度姿態測量的需求，必須進行畸變校正[5～8]，才能提高角度測量精度。向矢量。根據星點在上述兩個坐標系中方向矢量的對應關系，可以得到載體坐標系在慣性坐標系中的轉移矩陣，實現姿態確定。

畸變主要影響星點在載體坐標系下的方向矢量確定精度。理想的星敏感器成像模型為針孔模型，如圖1所示。

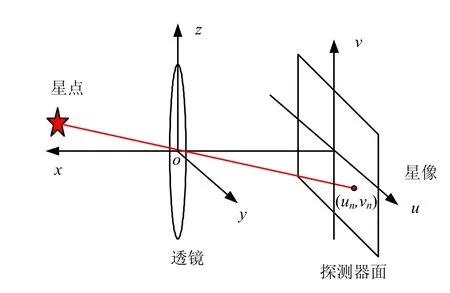
圖1 星敏感器理想成像模型

1 基于多項式擬合的畸變校正原理

1.1 星敏感器理想成像模型

星敏感器定姿的基本步驟為：a）從拍攝獲取的星圖中提取星點的坐標，根據星點坐標確定星點在星敏感器載體坐標系下的方向矢量；b）利用星圖匹配方法識別探測得到的星點，確定星點在慣性坐標系下的方

設星敏感器的載體坐標系為（x, y, z），星光經過光學系統在探測器面上形成彌散斑，通過星點提取算法計算其中心坐標為（un，vn），則恒星單位方位矢量在星敏感器載體坐標系下為

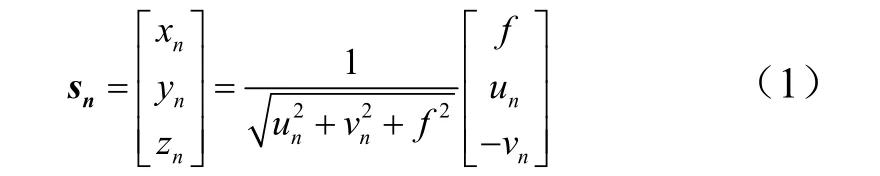
上述模型沒有考慮畸變的影響。在工程上，一方面焦距f難以精確測量，往往是經過試驗標定獲得。另一方面，由于畸變的存在，中心坐標與方向矢量的關系不滿足式（1），也需要標定。實際上往往采用兩者結合的綜合實驗法，重建方向矢量與星點坐標的關系。

1.2 多項式擬合的校正原理

從成像面的星像坐標點計算相應星光在星敏感器載體坐標系下的矢量，需要借助一種光學系統映射模型公式，該公式的系數通過標定試驗獲得。標定試驗通過1臺高精度二軸轉臺和1臺高精度平行光管來進行參數標定。

二軸轉臺按照既定規劃轉動N次，獲得N個相對于星敏感器載體坐標系的星光矢量[xn, yn, zn]，（n = 1, 2, …, N），同時記錄各次轉動的成像點亞像素坐標[un, vn]，（n = 1, 2, …, N），基于這2組數據進行如式（2）和式（3）所示的 5次多項式的最小二乘擬合，獲得 42個標定系數k0～k41。

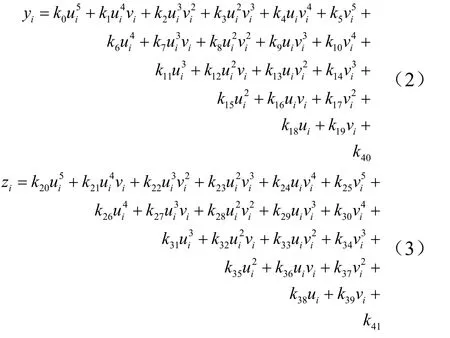
上述公式可以寫成矩陣形式，令：

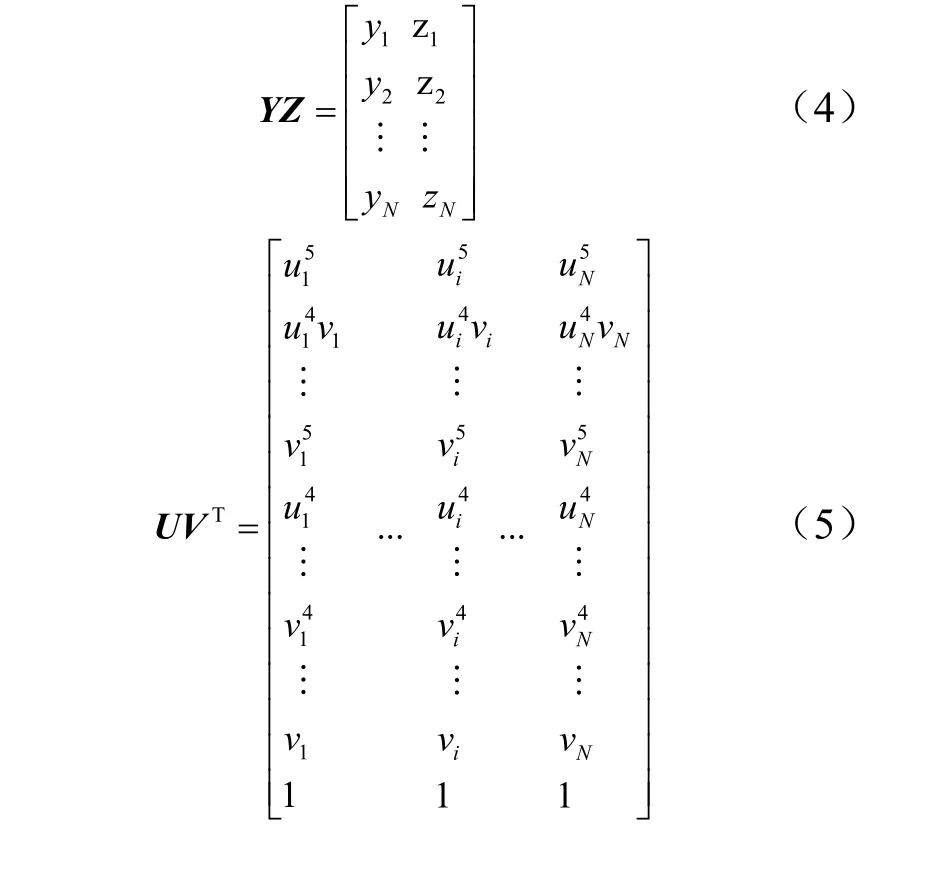
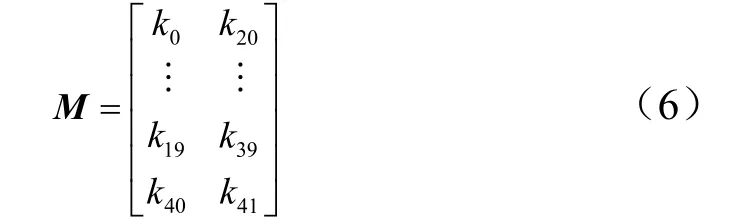
則式（2）、式（3）可以寫成矩陣形式：

利用最小二乘原理，已知矩陣YZ和UV，可以計算得到標定系數矩陣M。

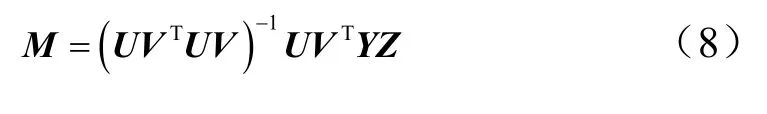
2 畸變測試及校正

2.1 畸變測試原理及過程

測試原理如圖2所示。測試設備主要由平行光管、目標分劃板、高精度二維電控轉臺（含控制系統）、星敏感器圖像處理系統和畸變計算軟件組成。

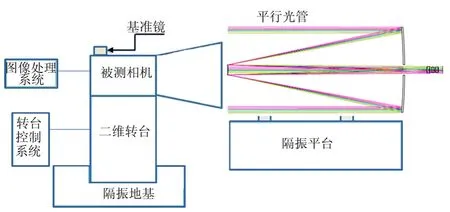
圖2 相機系統畸變測試示意

將星敏感器（圖 2中的被測相機）安裝在轉臺臺面，調整待測產品，使待測產品和平行光管中心基本在同一高度。測試時，在平行光管焦面放置星點板，控制轉臺水平運動，使星點在CCD靶面成像，記錄轉臺水平轉動的一系列標準角度ωi（i=1,2,3,…），同時相對應的待測產品采集圖像Pi（i=1,2,3,…），采集過程從相機的左片出現圖像開始，到右片圖像消失結束。控制轉臺俯仰在不同角度重復以上水平方向的掃描，最終在待測產品像面進行網格狀的全覆蓋測試。

對于本次畸變校正試驗，使用的二維電控轉臺方位角定位精度±0.8 ″，方位角重復精度0.2 ″；俯仰角定位精度±1.5 ″，俯仰角重復精度 0.3 ″。平行光管焦距950 mm，遠大于被測系統的焦距18 mm，光束的平行性小于3 ″，波像差優于 /15λ （λ=632.8 nm）。轉臺移動的角度間隔設為0.7°，每行移動21次，單行覆蓋14°，全幅面一共掃描 21×21=441各點，覆蓋14°×14°視場范圍。畸變測試現場如圖3所示。

圖3 畸變測試現場

部分測試數據結果如表 1所示。方向矢量與方位角α、俯仰角β關系如下：

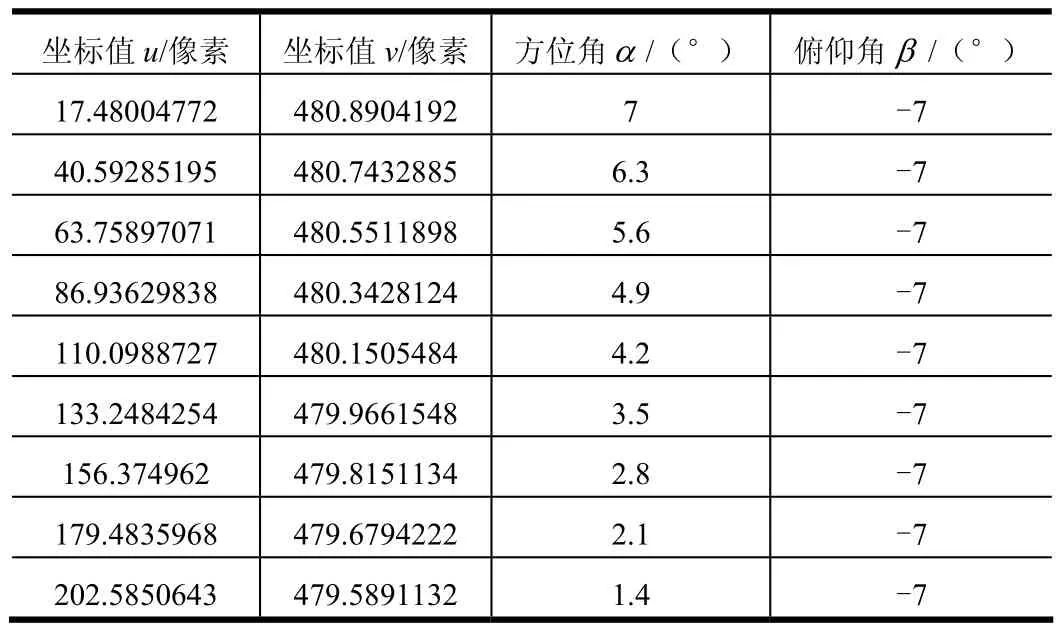
表1 畸變標定測試數據記錄（部分）

2.2 畸變校正結果

根據試驗得到的坐標數據與方位數據，可以計算得到校正系數，對畸變進行校正。校正后的畸變量計算有2種方式：a）采用焦距f；b）采用主距 f'。主距采用各個視場角ωi下測得的畸變量 yδ′平方和為最小值的方法計算得到：

式中 yi′為實測像高。視場角ωi與測量的方位角αi、俯仰角βi的關系為

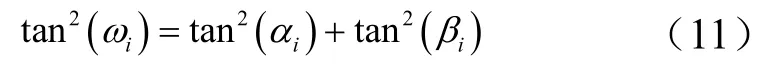
像高yi′的計算公式為

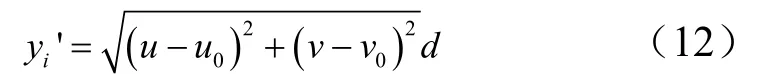
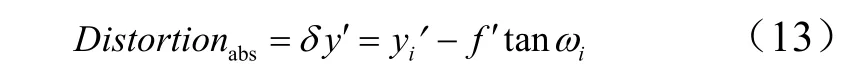
相對畸變定義為

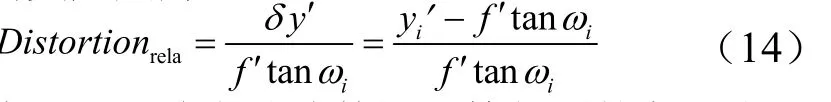
根據式（10）結合試驗數據計算得到的主距為 'f為18.902 mm，校正后的441個測試點的絕對畸變最大值為0.0 142 mm，對應的角度測量誤差為2.6 ′，相對畸變最大值為0.43%，平均值為0.16%。

本質上采用主距替代焦距利用式（1）進行方向矢量的計算也是一種畸變校正方法。采用主距校正畸變后的理論像點與實際像點位置如圖4所示。其中理論像點為利用主距以及轉臺的角度計算得到的值。

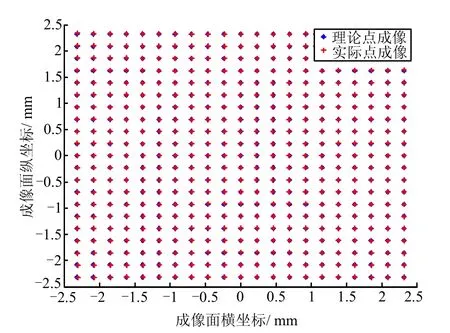
圖4 理論像點與實際像點偏差

采用多項式擬合法校正后的最大角度誤差為10 ″，平均角度誤差為 0.79 ″。可以看到，采用畸變校正系數法校正后的精度相對主點法大大提高。實際角度與多項式擬合校正后的測試角度對比如圖5所示。

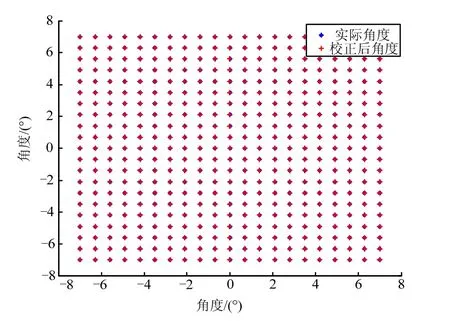
圖5 實際角度與多項式擬合校正后的測試角度對比

4 結 論

本文建立了基于多項式擬合的畸變校正模型，對

式中 d為像素的尺寸，取10 μm；u0，v0為光軸與探測面的交點坐標。利用校正公式，令y和z均為零，計算得到u0和v0的值。

對于星敏感器，系統的絕對畸變影響角距的測量誤差，絕對畸變定義為實測像高與理論像高之差：研制的星敏感器進行了標定試驗，利用測試數據得到了最終的校正系數，利用該校正系數可以完成畸變的校正，提高星敏感器的測量精度。需要說明的是，根據校正公式，可以依據星圖的質心坐標，直接解算星點在星敏感器坐標系下的方向矢量，而不需要焦距、像素尺寸信息，因為該校正公式已經把這兩個信息融合進去了。該方法與主點校正法相比精度大大提高，付出的代價只是增加了計算量，而且主要是乘法運算，對運算時間影響不大。

[1]梁斌, 朱海龍, 張濤, 等. 星敏感器技術研究現狀及發展趨勢[J]. 中國光學, 2016, 1(9): 16-29.

[2]劉壘, 張路, 鄭辛, 等. 星敏感器技術研究現狀及發展趨勢[J]. 紅外與激光工程, 2007, 36(S): 529-533.

[3]賀鵬舉, 梁斌, 張濤, 等. 大視場星敏感器標定技術研究[J]. 光學學報, 2011, 31(10): 1023001-1-1023001-7

[4]丁國鵬, 張濤, 鄭偉波, 等. 大視場星敏感器畸變校正技術[J]. 光學技術, 2015, 41(2): 97-100.

[5]佟帥, 李輝, 王安國. 多通道艦載星敏感器標定方法[J]. 光電工程, 2015, 42(2): 21-27

[6]李勉洪, 丁國鵬, 鄭偉波.大視場星敏感器標定技術[J]. 傳感器與微系統, 2015, 34(7): 40-44.

[7]鐘紅軍, 楊孟飛, 盧欣. 星敏感器標定方法研究[J]. 光學學報, 2010, 30(5): 1343-1348

[8]孫高飛, 張國玉, 鄭茹, 等. 星敏感器標定方法的研究現狀與發展趨勢[J]. 長春理工大學學報（自然科學版）, 2010, 33(4): 8-14.

A Distortion Correction Method for Large Field-of-view Star Sensor

Li Jian-hua1, Li Zhi-feng1, Niu Zhen-hong1, Zhao Qian1, Liu Jia-qi1,2
(1. National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing 100076；2. Beijing Institute of Space Long March Vehicle, Beijing,100076)

For wide field of view star sensor，the lens distortion will lead the deterioration in attitude measurement accuracy. A polynomial fitting distortion correction method is proposed to correct this distortion. By using this method, the average angle measure error is less than 1″.

Star sensor; Distortion Correction; Polynomial fitting

TP333

A

1004-7182(2017)01-0103-04

10.7654/j.issn.1004-7182.20170124

2016-04-01；

2016-07-01

李建華（1985-），男，工程師，主要研究方向為光學探測及光電對抗等技術