應用EMD和雙譜分析的故障特征提取方法*

蔣永華， 李榮強， 焦衛東， 唐 超， 蔡建程， 施繼忠

(浙江師范大學精密機械研究所 金華，321004)

?

應用EMD和雙譜分析的故障特征提取方法*

蔣永華， 李榮強， 焦衛東， 唐 超， 蔡建程， 施繼忠

(浙江師范大學精密機械研究所 金華，321004)

針對傳統雙譜分析從理論上僅能抑制高斯噪聲，但對非高斯噪聲無能為力的不足，提出了一種利用經驗模式分解(empirical mode decomposition, 簡稱EMD)和雙譜分析的故障特征提取方法，并應用于滾動軸承故障診斷中。首先，對信號進行EMD分解；其次，利用能量相關法去除EMD分解過程中出現的偽本征模態分量(intrinsic mode function, 簡稱IMF)；最后，對得到的真實IMF進行雙譜分析提取故障特征。仿真和實驗結果表明，所提出的方法優于功率譜分析和傳統雙譜分析，能夠更有效地提取強噪聲背景下的機械故障特征信息，為滾動軸承的故障特征提取提供了一種新的方法。

經驗模式分解; 雙譜分析; 能量相關; 特征提取; 本征模態分量

引 言

滾動軸承是旋轉機械中應用最為廣泛的機械零件，也是最容易損壞的元件之一[1]。在旋轉機械振動信號中，大量的信號是非平穩和非高斯分布的信號，尤其是在發生故障時更是如此[2]。然而，傳統的功率譜分析以及時頻分析不能反應頻率成分間的相位信息，通常也就無法處理非最小相位系統和非高斯分布信號，而高階譜尤其是雙譜分析是分析非平穩和非高斯信號的有力工具[3]。它從更高階概率結構表征隨機信號，彌補了二階統計量不包含相位信息的缺陷[4]，因此用雙譜分析振動信號更容易獲得有用的故障特征信息。但是，高階譜理論上能完全抑制高斯噪聲，對非高斯類噪聲卻無能為力[5]，而這些非高斯類噪聲的存在對信號的高階譜造成干擾，從而對故障特征的提取和分析造成不利影響。而機械故障信號中往往含有各種噪聲，信號的信噪比一般較低[6-7]，尤其是機器發生早期故障時，其故障信號非常微弱，如何從強噪背景中有效地提取出故障特征信息，直接影響著故障診斷的準確性以及故障早期預報的可靠性[8]。

為了解決上述問題，將EMD和雙譜分析相結合，提出了一種基于EMD和雙譜分析的故障特征提取方法。這一研究思路來源于兩種信號分析方法的各自特點，EMD可以有效處理信號中存在的非高斯噪聲，而雙譜分析理論上能完全抑制高斯噪聲。此外，由于在復雜的機械故障信號中，其故障信號往往處于低頻階段，而背景噪聲卻處于高頻階段，因此，先對信號進行分頻，再做雙譜分析，能更有效地提取出故障特征信息。而EMD恰好是一個從高頻到低頻逐次分解的基于信號本身的自適應時變濾波過程，其本質上是類似小波分解的、恒品質因數的二進帶通濾波器[9]。因此，先對信號進行EMD分解，將信號有效地從高頻到低頻進行分解[10-11]，但EMD分解過程中會產生偽IMF，直接影響后續雙譜分析。因此，采用能量相關法對IMF進行篩選去除偽分量，最后對得到的真實IMF進行雙譜分析提取出故障特征信息，仿真分析和實驗結果對其進行了驗證。

1 雙譜分析

(1)

(2)

由于零均值的高斯過程或非歪斜的非高斯過程的雙譜恒為零，故雙譜對高斯噪聲有很強的抑制能力，描述了過程或信號的高斯性和對稱性。

雙譜的估計方法有兩類，一類是間接由參數模型估計雙譜，另一類是直接由定義計算雙譜即快速傅里葉變換(fast Fourier transformation, 簡稱FFT)的三階周期圖法，這種直接法計算簡便、快速，因此采用直接法計算雙譜，具體過程如下。

2) 計算離散傅里葉變換系數

(3)

其中：λ=0,1,…,M/2;k=1,…,K。

3) 計算離散傅里葉變換系數的三重相關

(4)

其中：Δ0=fs/N0，而N0和L1應選擇為滿足M=(2L1+1)N0的值。

4) 所給數據x(0),x(1),…,x(N-1)的雙譜估計由K段雙譜估計的平均值給出，即

(5)

2 能量相關法去除偽IMF

EMD從本質上講就是通過對非平穩信號的分解，來獲得一系列表征信號特征時間尺度本征模態函數的一種方法。其中IMF必須滿足兩個條件：a.信號的極大值點與極小值點之和與過零點數目相等或最多相差一個；b.由局部極大值構成的上包絡線和由局部極小值構成的下包絡線的平均值為零。分解過程為：先找出信號x(t)的所有局部極值點，根據極值點插值得到信號的上、下包絡線，記上、下包絡線的平均值為m，則有

(6)

若差值函數h不是一個IMF，則將h作為x(t)代入式(6)重復上述過程，直到h是一個本征模態函數，此時提取出第一個IMF分量c1，則式(6)可寫為

(7)

把r1當作新數據重復以上步驟，得到各個IMF分量ci，i=1,2,…,n，以及余量rn，當rn為單調函數或者其幅度小于預先給定的閥值時，則停止分解。此時，余量rn就是趨勢項r，這樣，就把信號x(t)分解成n個本征模態函數和一趨勢項。即

(8)

在EMD過程中，由于存在端點效應的影響，會產生偽本征模態函數，不利于對故障特征信息的提取，嚴重影響到后期故障診斷的準確性。為去除無用的偽本征模態函數，采用能量相關方法來鑒別真偽。

EMD分解出的IMF，其本質上是原信號的組成成分，理論上所有IMF的能量之和應等于原始信號的能量，即每一個IMF的能量應和原始信號的能量極大相關，而分解產生的偽分量能量與原始信號能量應極小相關，這樣根據能量相關性的大小篩選真實的IMF。具體過程為，首先計算信號x(t)能量

(9)

分別計算每個IMF的能量

(10)

根據互協方差函數可得

(11)

相應的相關程度系數為

(12)

由于偽本征模態函數能量與原始信號能量極小相關，所以式(12)值應較小，甚至接近于零，至此，則可以根據能量相關系數ρE篩選出真偽IMF分量。

下面以一個仿真信號為例來驗證能量相關法去除偽IMF分量的有效性。仿真信號x(t)如下

(13)

仿真信號x(t)由兩個正弦信號的疊加，頻率分別為10和30Hz，幅值均為1.5。

圖1為仿真信號x(t)進行EMD分解所得結果，其中第1，2個IMF分別對應原始信號10和30Hz的頻率成分，而第3，4個IMF則為偽分量，第5個信號r為趨勢項。由此可見，EMD分解由于受端點效應的影響會產生偽分量，使分解出的模式分量存在失真。

圖1 仿真信號的EMD分解結果Fig.1 EMD decomposition result of the simulated signal.

對每個IMF與原始信號做能量相關計算得到的結果如表1所示。從表1中可以看出，第1,2個IMF與原始信號的能量相關系數較大，是原始信號的真實成分，并且反應了原始信號的特征；而第3,4個分量是由于EMD本身存在的端點效應而產生的偽分量，故其與原始信號的能量相關度很小。可以看出，本研究所提出的能量相關法能有效地篩選出真實的IMF，從而去除偽IMF分量。

表1 仿真信號各個IMF分量的能量相關系數

Tab.1 Energy-related coefficients of IMFs of the simulated signal

IMFsc1c2c3c4rρE/%72．870．8415．3610．48．06

3 基于EMD和雙譜分析的故障特征提取

對信號進行EMD分解，EMD能根據信號中不同時間尺度的波動自適應的逐級分解，將信號從高頻到低頻進行分頻，高頻噪聲最先分解出，而機械振動故障信號往往出現在低頻，再根據能量相關篩選出真實有用的IMF分量，最后對其進行雙譜分析，提取故障特征信息。基于EMD和雙譜分析的故障特征提取方法的基本流程如圖2所示。

圖2 基于EMD和雙譜分析的故障特征提取流程簡圖Fig.2 Flowchart of method based on EMD and bispectrum

對于工程實際中的旋轉機械振動信號，如滾動軸承故障信號，當出現故障時，軸承的其他零件會周期性地撞擊故障處，形成一系列由沖擊激勵產生的減幅振蕩。根據故障特征頻率可以診斷出故障位置，但由于沖擊振動的能量散布在一個比較寬的頻帶上，其頻譜包含故障特征頻率的各次諧波，非常容易被噪聲淹沒，難以直接觀察。因此，先用EMD對其進行分頻，再對篩選出的IMF作雙譜分析。

對一滾動軸承外圈故障信號進行分析，實驗對象為NU205型滾動軸承，節徑為38.5 mm，滾動體直徑7.5 mm，滾動體數目12個，接觸角0°，采樣頻率4 000 Hz，采樣長度1 024點。軸承實驗臺由電機帶動輸入軸，轉速控制在800 r/min，輸出軸帶動負載。在軸承外圈加工寬0.18 mm、深0.28 mm的小槽模擬軸承外圈裂紋和斷裂故障。經計算可知，外圈故障頻率為64.4 Hz。

采用本方法對其進行分析，先對信號進行EMD分解，得到的結果如圖3所示。其中c1,c2分量為滾動軸承故障振動信號的高頻成分，不包含軸承的故障特征頻率，可以直接剔除[12]。再對c3～c8IMF分量進行能量相關計算，得到的結果如表2所示。

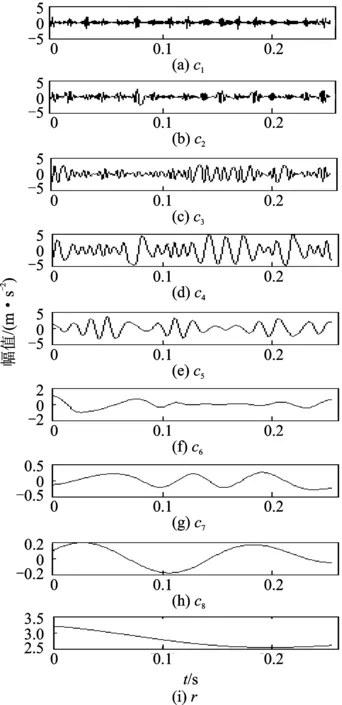
圖3 滾動軸承故障信號EMD分解結果Fig.3 EMD decomposition result of rolling bearing signal

表2 軸承信號各IMF分量的能量相關度系數

從表2中看出，后3個分量(即c6～c8)為偽分量，因此將其剔除。最后，對真實有用的IMF分量(即c3～c5)進行雙譜分析，得到的譜圖如圖4所示。

從圖4(a,b)中可以看出，其頻率主要出現在(128，128Hz)，(-128，128Hz)(-128，-128Hz)以及(128，-128Hz)，(64，64Hz)，(-64，64Hz)，(-64，-64Hz)和(64，-64Hz)處，而圖4(c)中則主要出現在相應4個象限的52Hz處。由于譜圖的聚集性等原因，頻率沒有精確到0.1Hz，因此說頻率主要出現在64, 128Hz處，嚴格來說頻率主要出現在64, 128Hz附近，包括64.4, 128.8Hz。所以，不但反應出了滾動軸承主要故障特征頻率以及相應的倍頻成分，而且也反應出了信號的相位特征。因此，本方法可以有效提取出強噪背景下的故障特征信息。

4 本方法與傳統方法比較

對其進行功率譜分析和傳統的雙譜分析，結果分別如圖5和圖6所示。

圖5 滾動軸承故障信號的功率譜分析 Fig.5 The power spectral of rolling bearing fault signal

圖6 滾動軸承故障信號的傳統雙譜分析Fig.6 The power spectral of rolling bearing fault signal

由圖5和圖6可知，由于受到噪聲干擾的影響，無法從其功率譜分析和傳統雙譜分析中識別出滾動軸承的故障特征頻率，其故障特征頻率被完全淹沒于強噪聲背景中，故傳統的功率譜分析方法和常規雙譜分析方法在提取滾動軸承故障特征時存在著明顯的不足。相比圖4可知，采用本方法分析不但正確反應出了滾動軸承主要故障特征頻率64Hz以及相應的倍頻成分128Hz，而且也反應出了信號的相位特征。因此，相比傳統的功率譜分析和傳統雙譜分析，本方法可以更有效地提取出強噪背景下的故障特征信息，這為滾動軸承的故障診斷提供了一種新的途徑。

5 結束語

利用EMD對信號進行分頻去除高頻噪聲，再采用能量相關法篩選出真實的IMF，最后對真實IMF進行雙譜分析，能夠有效地反映出故障特征頻率，提取故障特征信息。仿真試驗和實際軸承數據的分析結果表明了本方法的正確性與可行性，筆者還將本方法與功率譜分析和常規雙譜分析方法進行了對比，表明本方法能更有效地提取強噪聲背景下的機械故障特征信息。

[1] 李軍偉, 韓捷, 李志農, 等. 小波變換域雙譜分析及其在滾動軸承故障診斷中的應用[J]. 振動與沖擊, 2006, 25(5): 92-95.

Li Junwei, Han Jie, Li Zhinong, et al. Bispectrum analysis in the wavelet transform domain and its application to the fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2006, 25(5): 92-95.(in Chinese)

[2] 李凌均, 韓捷, 李朋勇, 等. 矢雙譜分析及其在機械故障診斷中的應用[J]. 機械工程學報, 2011, 47(17): 50-54.

Li Lingjun, Han Jie, Li Pengyong, et al. Vector-bispectrum analysis and its application in machinery fault diagnosis [J]. Journal of Mechanical Engineering, 2011, 47(17): 50-54.(in Chinese)

[3] 趙子煒, 艾紅. 高階譜在滾動軸承故障診斷中的應用[J]. 煤礦機械, 2015, 36(7): 303-305.

Zhao Ziwei, Ai Hong. Fault diagnosis of rolling bearing using higher-order spectrum [J]. Coal Mine Machinery, 2015, 36(7): 303-305.(in Chinese)

[4] 陳峙, 王鐵, 谷豐收, 等. 基于電動機電流信號的雙譜分析的齒輪傳動故障診斷[J]. 機械工程學報, 2012, 48(21):84-90.

Chen Zhi, Wang Tie, Gu Fengshou, et al. Gear transmission fault diagnosis based on the bispectrum analysis ofinduction motor current signatures[J]. Journal of Mechanical Engineering, 2012,48(21):84-90.(in Chinese)

[5] 嚴可國, 柳亦兵, 徐鴻, 等. 基于雙譜分析的大型汽輪機振動故障特性提取[J]. 中國電機工程學報, 2010, 30(2): 98-103.

Yan Keguo, Liu Yibing, Xu Hong, et al. Fault feature extraction of large steam turbine based on bispectra analysis of vibration signal[J]. Proceedings of the CSEE, 2010, 30(2): 98-103.(in Chinese)

[6] Jiang Yonghua, Tang Baoping, Qin Yi, et al. Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD[J].Renewable Energy, 2011, 36(8):2146-2153.

[7] 湯寶平, 蔣永華, 姚金寶. 基于重分配魏格納時頻譜和SVD的故障診斷[J]. 振動、測試與診斷, 2012,32(2):301-305.

Tang Baoping, Jiang Yonghua, Yao Jinbao. Fault diagnosis based on reassigned Wigner-Ville distribution spectrogram and SVD [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(2):301-305.(in Chinese)

[8] Liu B, Riemenschneider S, Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum [J].Mechanical Systems and Signal Processing, 2006, 20: 718-734.

[9] Cheng Junsheng, Yu Dejie, Yang Yu. A method for gear fault diagnosis based on the empirical mode decomposition [J]. Internationl Journal of Plant Engineering and Management, 2004, 4(9): 230-235.

[10]張志剛,石曉輝,施全, 等. 基于改進EMD和譜峭度法滾動軸承故障特征提取[J]. 振動、測試與診斷, 2013, 33(3): 478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 478-482.(in Chinese)

[11]焦衛東,蔣永華,林樹森. 基于經驗模態分解的改進乘性噪聲去除方法[J]. 機械工程學報, 2015, 51(24): 1-8.

Jiao Weidong, Jiang Yonghua, Lin Shusen. Modified signal de-noising approach for multiplication noise based on empirical mode decomposition [J]. Journal of Mechanical Engineering, 2015, 51(24): 1-8.(in Chinese)

[12]湯寶平,蔣永華,張詳春. 基于形態奇異值分解和經驗模態分解的滾動軸承故障特征提取方法[J]. 機械工程學報, 2010, 46(5): 37-42.

Tang Baoping, Jiang Yonghua, Zhang Xiangchun. Feature extraction method of rolling bearing fault based on singular value decomposition-morphology filter and empirical mode decomposition [J]. Journal of Mechanical Engineering, 2010, 46(5): 37-42.(in Chinese)

*國家自然科學基金資助項目(51405449，51575497)；浙江省公益技術應用研究計劃項目資助項目(2016C31067)。

2016-03-10；

2016-08-03

10.16450/j.cnki.issn.1004-6801.2017.02.021

TH165.3；TN911.2

蔣永華，男, 1982年4月生, 博士、副教授。主要研究方向為機械設備狀態監測與故障診斷、測試計量技術及儀器等。曾發表《Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD》(《 Renewable Energy》2011, Vol.36,No.8)等論文。 E-mail:yonghua_j82@126.com