考慮模型形式誤差的轉子動力學修正及確認*

張保強, 郭勤濤， 袁修開

(1.廈門大學航空航天學院 廈門，361005) (2.南京航空航天大學機電學院 南京，210016)

?

考慮模型形式誤差的轉子動力學修正及確認*

張保強1, 郭勤濤2， 袁修開1

(1.廈門大學航空航天學院 廈門，361005) (2.南京航空航天大學機電學院 南京，210016)

研究考慮模型形式誤差的軸承-轉子系統工作轉速下的動力學模型修正和確認方法。首先，介紹了模型形式誤差以及基于復模態特征值靈敏度的模型修正理論；然后，在此基礎上以軸承-柔性轉子系統為仿真算例，考慮模型形式誤差，使用系統在恒定工作轉速下的渦動頻率和阻尼參數，同時對軸承的支承剛度、支承阻尼和轉盤的直徑轉動慣量參數進行修正；最后，通過不平衡響應結果對修正模型進行了確認。仿真結果顯示，考慮模型形式誤差時的修正參數最大誤差仍有-10.1%，而修正后特征值實部最大誤差為0.95%，特征值虛部最大誤差為-1.15%，修正后不平衡響應與目標模型基本重合。研究表明，考慮模型形式誤差時軸承-轉子系統的修正方法是穩健的，也是有效可行的。

模型修正； 模型形式誤差； 轉子動力學； 工作轉速； 確認

引 言

結構動力學模型修正技術已經廣泛應用在航空航天、機械工程和土木工程等各個領域，根據其修正對象一般可以分為矩陣型和設計參數型兩種，而后者物理意義明確，因此更有益于實際工程應用[1]。對于工程中的很多旋轉機械，比如航空發動機中的軸承-轉子系統等，其動力學設計需要提供準確的模型[2]，因此也需要對軸承-轉子系統的動力學模型進行修正。

傳統有限元模型修正一般都是基于實模態參數進行的[3-5]，但對于旋轉機械，考慮到支承阻尼參數和陀螺效應的影響，不得不采用復模態理論求解[6-7]和修正。基于復模態特征參數的模型修正方法，正在逐步開展[8-13]。文獻[8-12]都是針對矩陣型模型修正展開研究的，其中文獻[12]給出了含阻尼有限元模型的修正方法，該方法雖然保證了矩陣的稀疏性，但仍屬于矩陣型模型修正，不易于工程設計中的參數修改和優化。Yuan等[13]采用實驗非完備復特征參數將模型修正轉化為約束最優化問題，同時修正模型的剛度、阻尼和陀螺矩陣，得到了滿足特征方程的最優矩陣，但此修正方法仍然屬于矩陣型模型修正，物理意義不明確，同樣不利于工程應用。

對于軸承-轉子系統的動力學模型修正，趙斌等[14]使用單盤轉子系統的前四階固有頻率為殘差，基于粒子群優化算法對轉子的材料彈性模量和兩個軸承參數進行了修正。Miao等[15]以雙轉子結構的前六階固有頻率為殘差，分別建立了一維和三維轉子有限元模型，對雙轉子四個區域部分材料的彈性模量進行了修正，并對修正后的模型進行了臨界轉速和不平衡響應的確認。張保強等[16]基于實驗復模態參數和靈敏度分析技術，對磁軸承-轉子系統的支承參數進行了識別研究。Xu等[17]使用軸的前四階共振頻率和MAC殘差，對磁懸浮軸承-轉子系統的軸模型進行了修正，并通過頻響函數進行了驗證。Chouksey等[18]考慮到滑動軸承支承參數隨轉速變化而發生變化的事實，改進了一種基于復模態特征靈敏度的方法，對滑動軸承參數進行了識別。Cavalini等[19]以軸承-轉子系統的頻響函數為殘差，提出了自適應差分進化算法。

當同時考慮阻尼和陀螺效應時，會大大增加軸承-轉子系統動力學模型修正的困難。此外，目前軸承-轉子系統動力學模型都是基于轉子本身或者軸承-轉子系統零轉速下的模態參數進行修正的，而實際系統在工作轉速下，系統渦動頻率和阻尼參數會發生改變，軸承支承參數也是動態變化的，因此需要發展一種使用工作轉速下的模態參數對軸承-轉子系統進行修正的方法。另一方面，對于軸承-轉子系統模型修正，一般都是分步、分層展開的[20]，因此需要考慮每一步修正后模型的誤差對下一層修正的影響，也就是在模型修正中需要考慮模型形式誤差的影響。

基于系統工作轉速下的模態參數，研究適合應用于工程實際軸承-轉子系統模型修正方法。通過一軸承-轉子系統的仿真算例，考慮轉子材料彈性模量存在模型形式誤差，使用1 600 r/min時的渦動頻率和阻尼參數，同時修正軸承的支承剛度、支承阻尼和轉盤的直徑轉動慣量等參數，驗證所提出方法的穩健性和有效性，最后通過不平衡響應對修正模型進一步確認。

1 基本理論

1.1 模型形式誤差介紹

模型形式誤差是在構造數學或力學模型過程中引入的，是一類關于模型本身的誤差。這種誤差主要是為了減少構造模型的復雜度而引入的簡化假設引起的，而這些簡化假設的引入不能通過改變參數來減小，因此模型形式誤差屬于認知不確定性[21-22]。

本研究所考慮的模型形式誤差，是指在分層或分步模型修正過程中，子部件結構動力學模型修正后所包含的模型或參數誤差。對于軸承-轉子系統而言，首先需要對軸本身的模型進行修正，即使修正后，軸的結構動力學模型仍然存在模型形式誤差。筆者主要研究軸本身存在的模型形式誤差在軸承-轉子系統動力學模型修正中的影響。

1.2 復模態有限元模型修正

基于復模態的有限元模型修正通常看作是一個優化問題

(1)

其中：p為設計參數向量；VLB和VUB分別為設計參數的邊界；ε為特征量的殘差。

(2)

為實驗測試和有限元計算特征值之間的殘差向量。而

(3)

(4)

其中：αE，ωE分別為實驗測試得到的特征值的實部和虛部；αA,ωA分別為有限元計算得到的復模態特征值的實部和虛部；εα(p),εω(p)分別為特征值實部和虛部的殘差向量。

基于靈敏度的有限元模型修正中

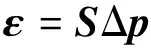
(5)

因此

(6)

其中：Δp為參數的改變量；S為特征量的一階靈敏度矩陣；S+為靈敏度矩陣S的廣義逆。

而基于復模態靈敏度分析的設計參數型模型修正方法的實現是一個迭代的過程，其主要步驟可參考文獻[16]。

1.3 復模態特征值靈敏度

在欠阻尼情況下，復模態特征方程對應的特征值為

(7)

其中：i=1,2,…,N；λi為第i階特征值；αi，ωi分別為特征值λi的實部與虛部。

(8)

復模態特征方程對設計參數求導數，可得特征值的一階偏導數[23]

(9)

其中：M為質量矩陣；K為剛度矩陣；Cd為阻尼矩陣，它們都為對稱矩陣；G為陀螺矩陣，是反對稱的。

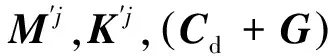
1.4 模態匹配及相關分析

有限元模型修正中，當采用頻率為響應特征時，在迭代過程中常常出現模態階次跳動的情況而使得有限元計算與實驗之間的目標頻率匹配錯亂。所以振型相關系數(modalassurancecriterion，簡稱MAC)，即模態置信度，常常用來解決模態匹配問題，達到模態跟蹤的目的。

振型相關系數是相關分析中的一種，用來表示兩個模型之間的模態振型相似程度，它是一個介于0～1之間的標量。當振型相關系數值為1時，代表兩個振型完全相關；當值為0時，表示兩個振型線性無關。文中的修正方法中引入振型相關系數只是為了得到特征值的正確匹配。

2 軸承-轉子系統模型修正

為了驗證所提出模型修正方法的正確性和有效性，采用一個軸承-柔性轉子系統的仿真修正進行驗證。

2.1 軸承-轉子系統有限元模型

考慮不對稱單盤軸承-轉子系統[24]如圖1所示，l1=2.40 m，為兩個軸承之間距離；l=3.0 m，為轉子的總長度；kxx1，cxx1，kyy1，cyy1；kxx2，cxx2，kyy2，cyy2分別為兩軸承徑向剛度和阻尼參數。

圖1中，轉子直徑d=0.16 m，轉子材料的彈性模量初始值E=210 GPa，密度為7 850 kg/m3，泊松比為0.3。單盤直徑為1.5 m，厚為0.06 m。仿真計算中將兩軸承的阻尼看作相等，即cxx1=cxx2=cxx；

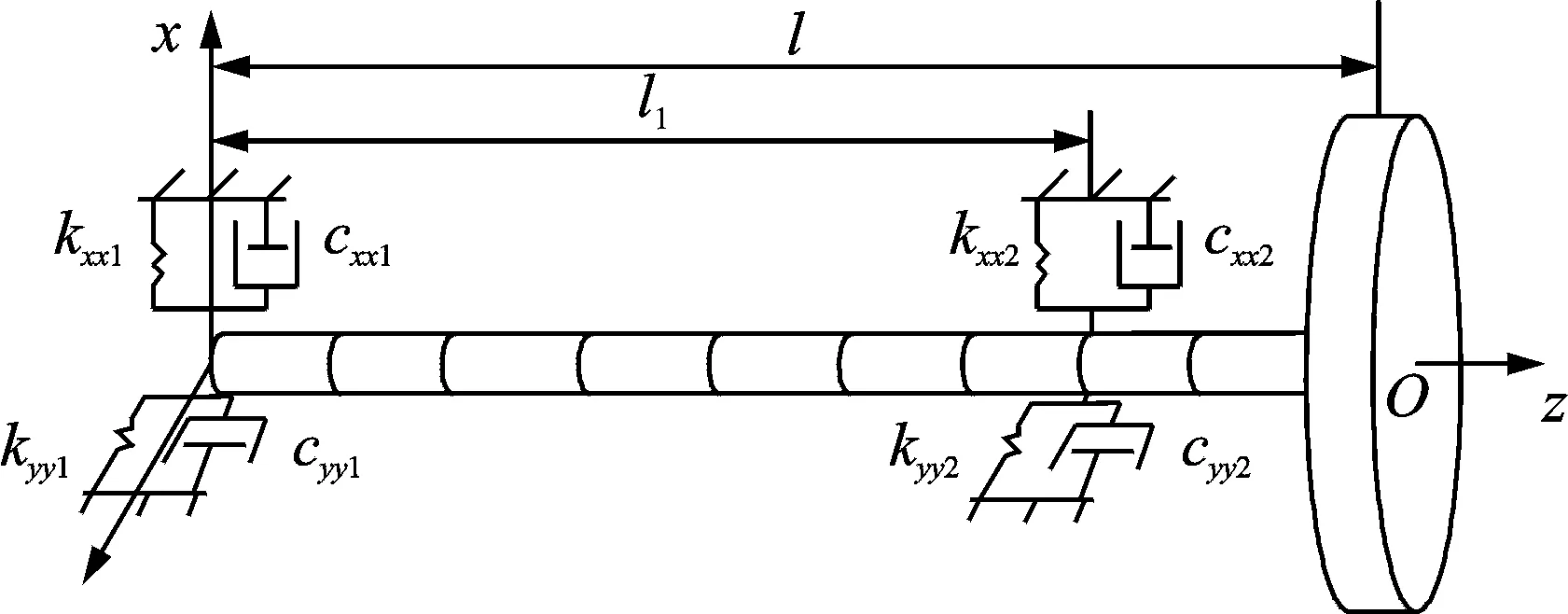
圖1 軸承-轉子系統有限元模型示意圖Fig.1 A finite element Bearing-rotor model

cyy1=cyy2=cyy。兩軸承支承參數的初始和目標值列于表1中。根據單盤的尺寸和材料，可以得到轉盤的質量m=828.9 kg，極轉動慣量Jp=322.22 kg·m2，直徑轉動慣量Jd=117.1 kg·m2。

采用通用有限元軟件Nastran中的一維梁單元建立轉子有限元模型，軸承的剛度和阻尼參數采用Bush單元模擬，盤采用集中質量單元簡化。系統有限元模型共包含21個節點。應用Nastran中的轉子動力學模塊計算得到系統在1 600 r/min時的各階渦動頻率。表1給出了仿真算例參數初值和修正結果。在迭代過程中使用相對值為修正參數，例如kxx1初始值為1．0×5．2×107N/m,目標值為1．2×5．2×107N/m。表2列出了系統前7階復特征值，其中初始值和目標值分別對應表1中參數的相應取值。

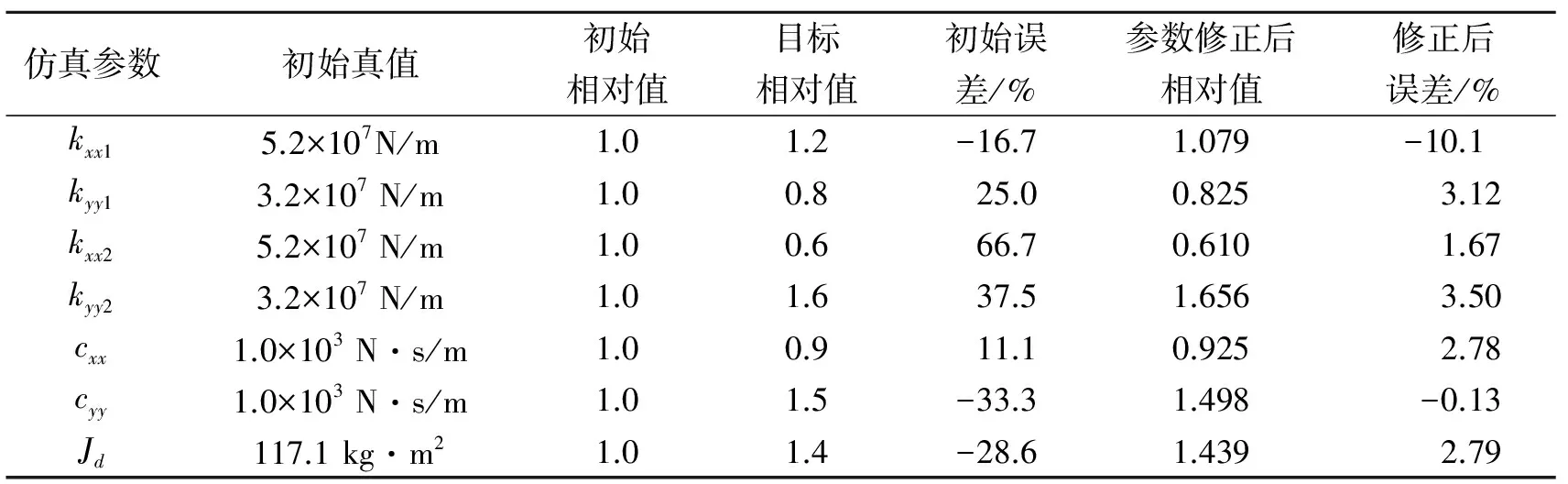
表1 仿真參數初始值、目標值和修正值比較

表2 1 600 r/min時系統各階渦動特征值及修正前后誤差

Tab.2 The wheel eigenvalue and errors for initial and updated model in 1 600 r/min

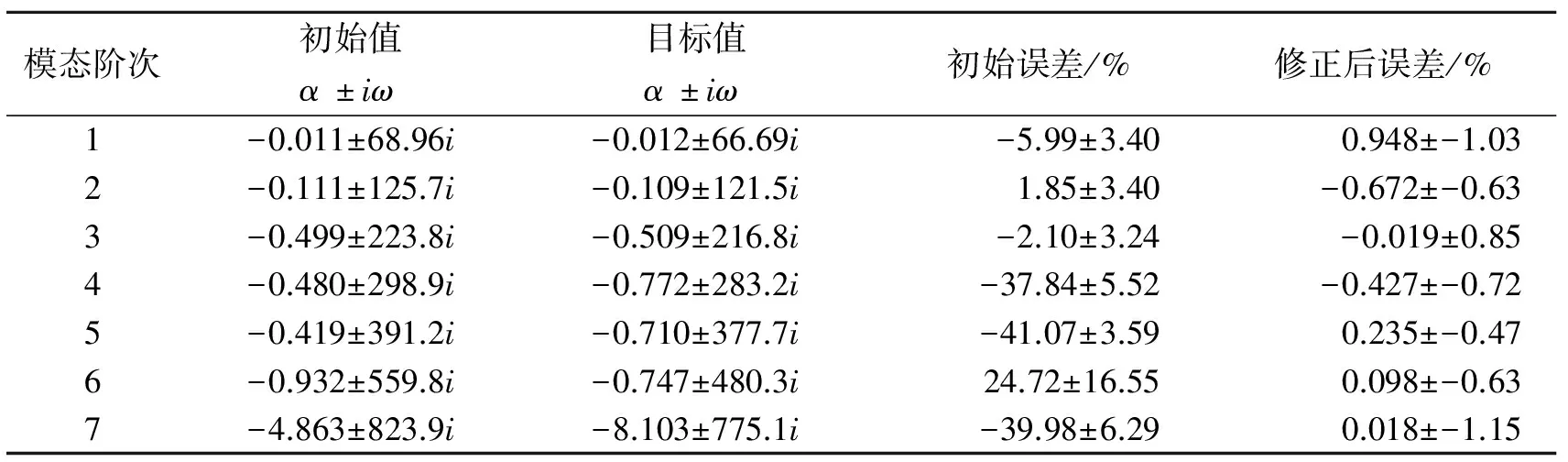
模態階次初始值α±iω目標值α±iω初始誤差/%修正后誤差/%1-0．011±68．96i-0．012±66．69i-5．99±3．400．948±-1．032-0．111±125．7i-0．109±121．5i1．85±3．40-0．672±-0．633-0．499±223．8i-0．509±216．8i-2．10±3．24-0．019±0．854-0．480±298．9i-0．772±283．2i-37．84±5．52-0．427±-0．725-0．419±391．2i-0．710±377．7i-41．07±3．590．235±-0．476-0．932±559．8i-0．747±480．3i24．72±16．550．098±-0．637-4．863±823．9i-8．103±775．1i-39．98±6．290．018±-1．15

2.2 修正中的模型形式誤差

對軸承-轉子系統的模型修正，一般都是采用分層策略執行的，即首先根據轉子結構的自由-自由狀態下的實驗測試數據修正轉子的結構參數，得到精確的轉子結構有限元模型后再根據轉子實際工作狀態修正系統中軸承等其他的不確定性參數。

此算例中假設已經對轉子自由-自由狀態的有限元模型進行了修正，并且假定修正后的轉子材料的彈性模量仍然存在2%的誤差。

對于轉子自由-自由狀態的模型修正而言，轉子材料的彈性模量參數為修正參數，屬于參數不確定性。而該參數在軸承-轉子系統整體動力學模型修正時，并沒有再作為修正參數，因此彈性模量的2%的誤差就成為整體軸承-轉子系統模型修正中的模型形式誤差，并且不能通過修正其他參數減少該模型形式不確定性。

2.3 考慮模型形式誤差的修正

在軸承-轉子系統動力學模型修正中，選擇兩個軸承各自的支承參數，以及盤的直徑轉動慣量等7個參數作為修正參數(見表1)。修正目標選擇前7階特征值的殘差。

模型修正的程序通過Matlab自動調用Nastran來實現，基于二次規劃(quadratic programming，簡稱QP)優化方法迭代計算，迭代過程中使用MAC匹配選擇正確的特征值目標計算殘差。具體流程如圖2所示。

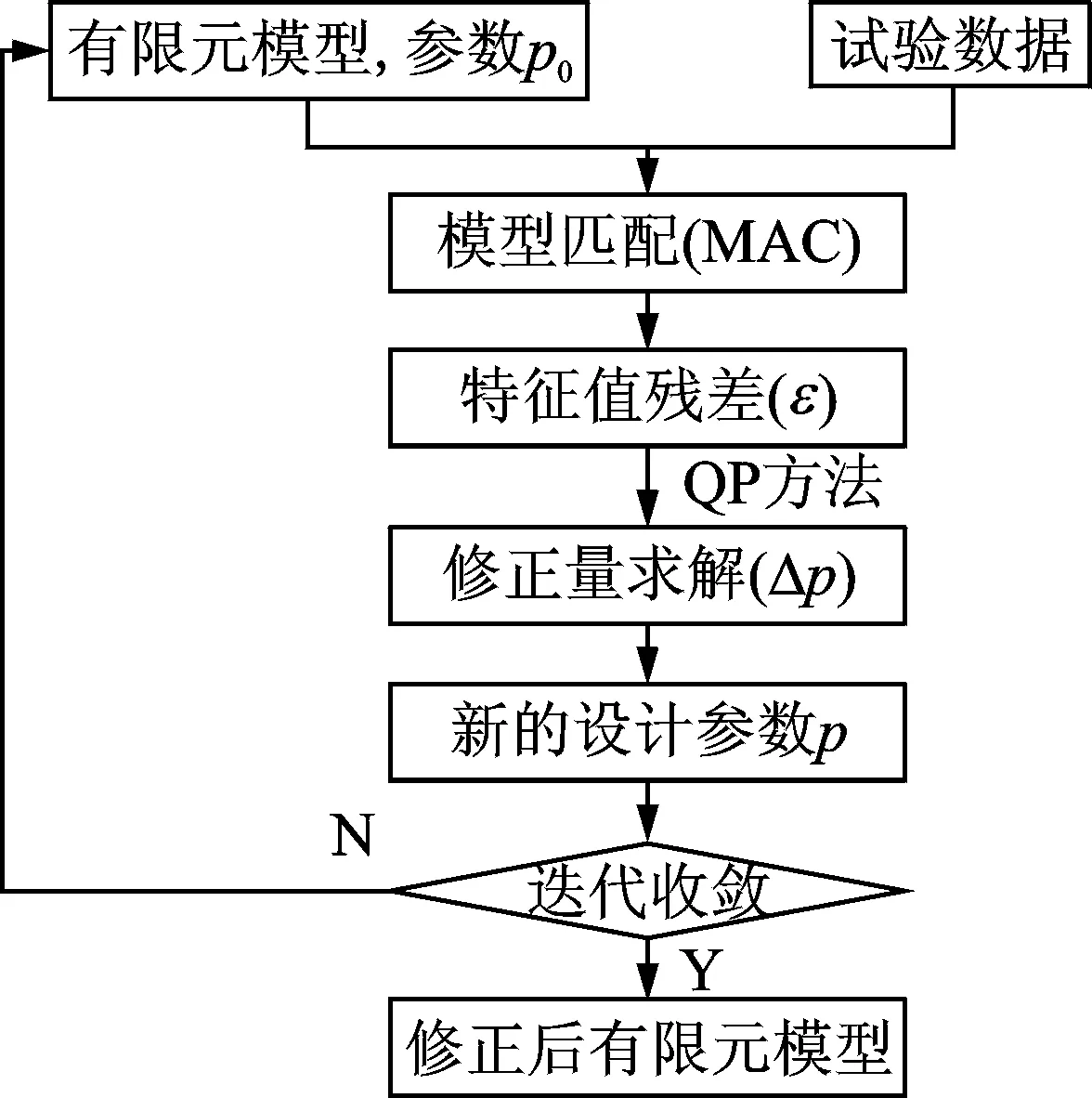
圖2 模型修正實現流程Fig.2 A flow chart of model updating

圖3～圖5分別給出了修正參數、特征值實部相對誤差及特征值虛部相對誤差的收斂情況。修正前后系統各階渦動特征值的比較情況列于表2中。

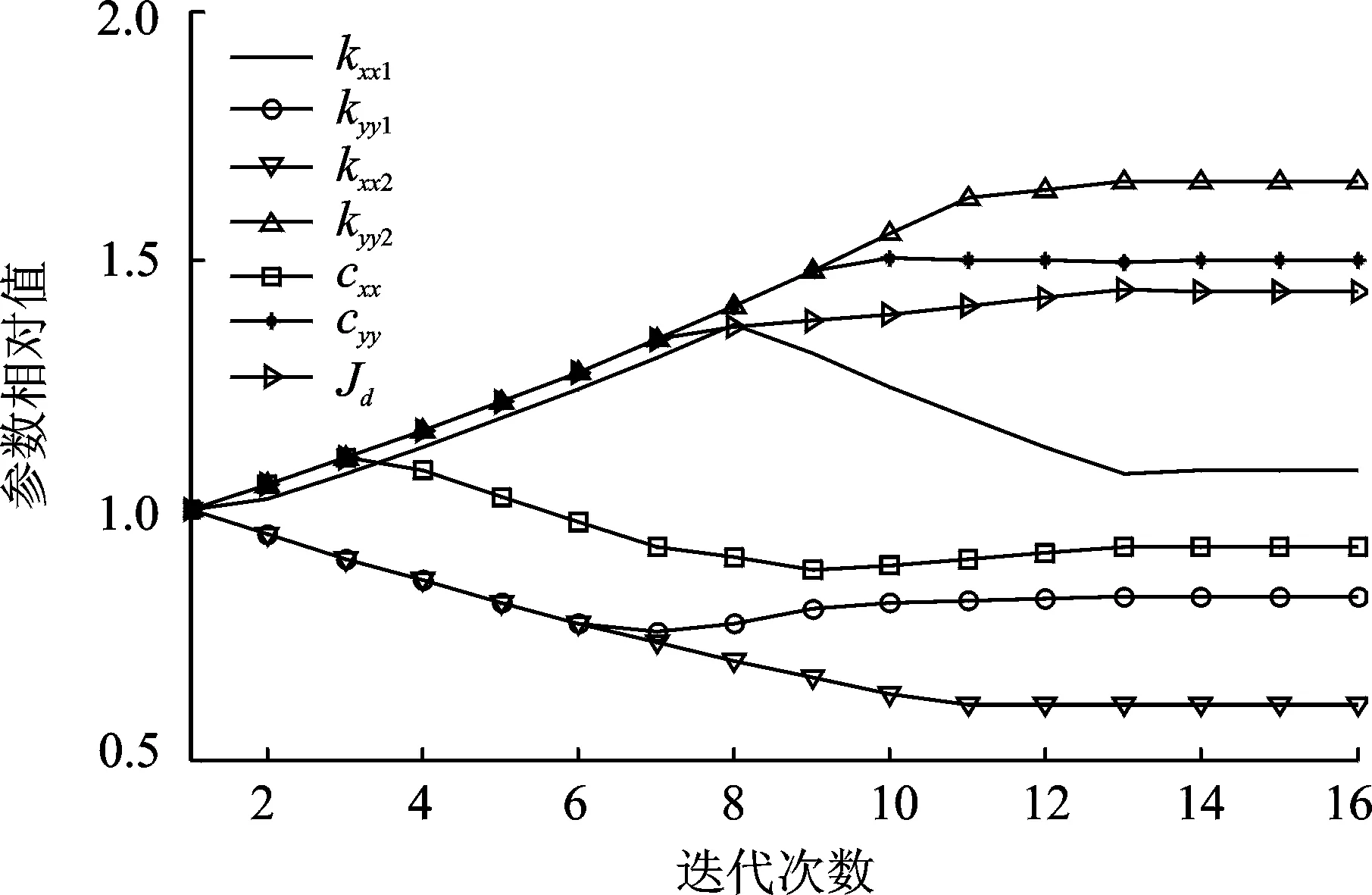
圖3 仿真參數收斂情況Fig.3 The convergence curve of the parameters

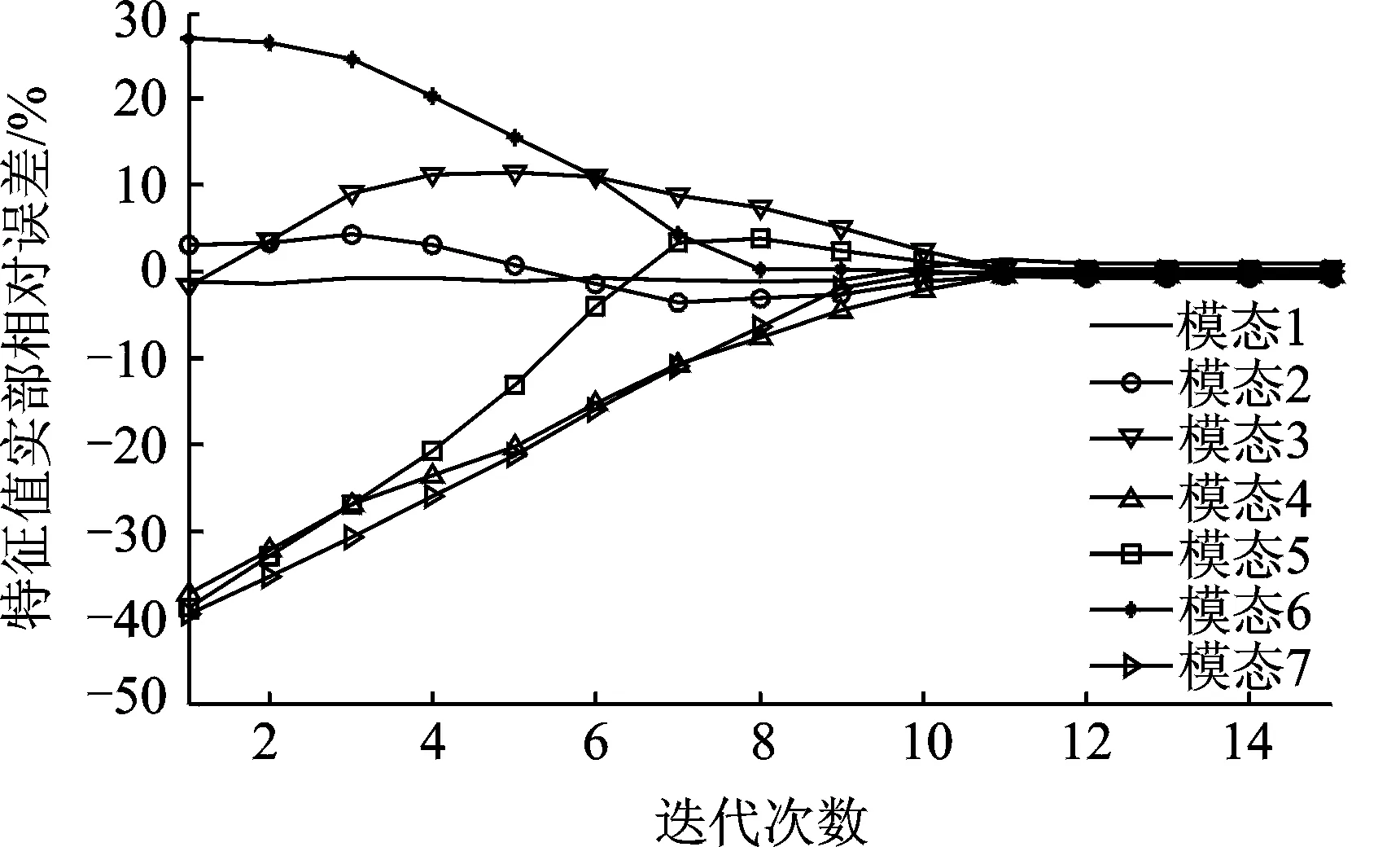
圖4 特征值實部收斂曲線Fig.4 The convergence curve of the real part of the eigenvalue

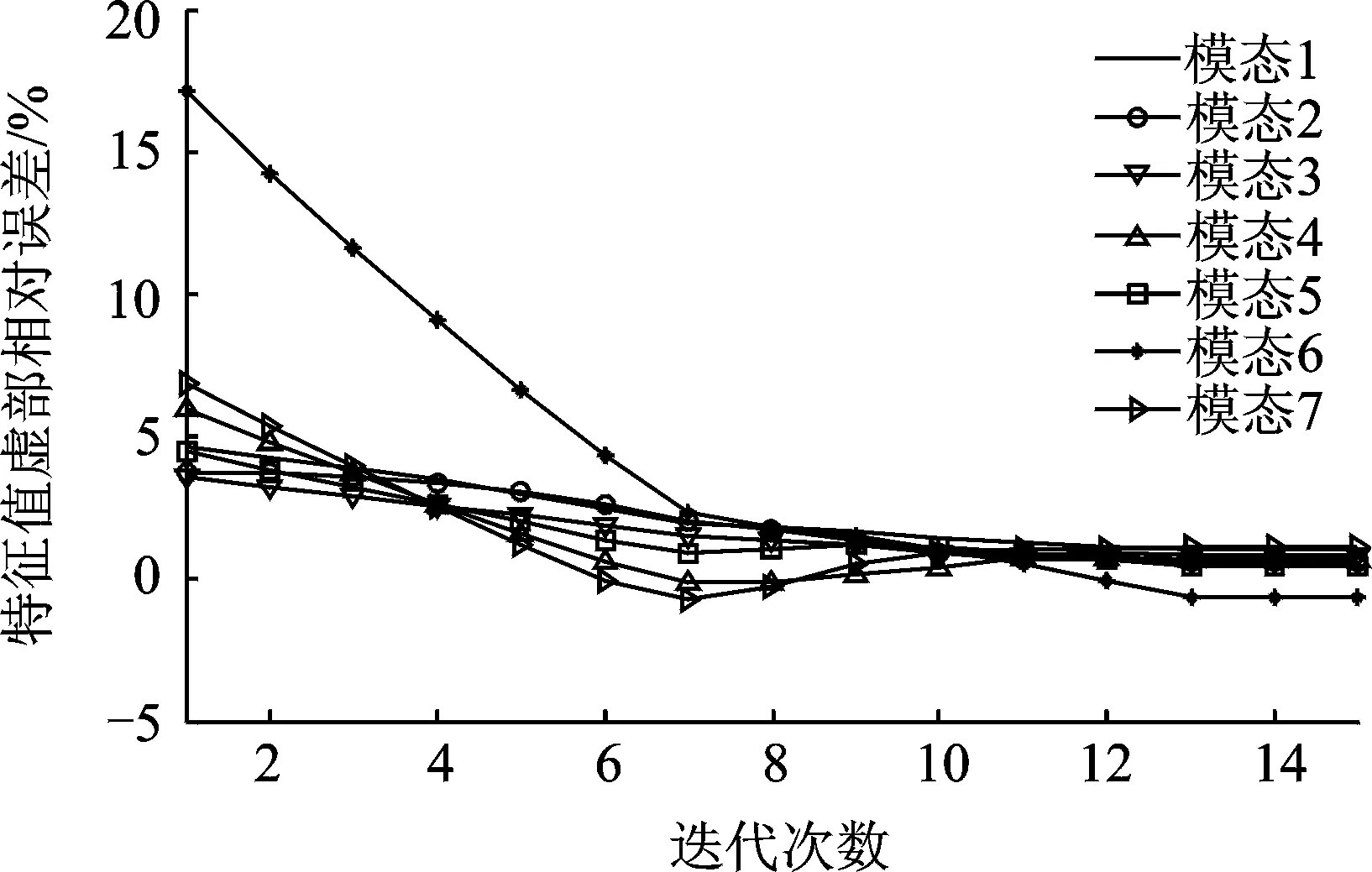
圖5 特征值虛部收斂曲線Fig.5 The convergence curve of the imaginary part of the eigenvalue

從表1中參數的修正結果，表2中特征值的修正誤差以及圖3～圖5的迭代情況可知，在修正迭代10步左右時，修正參數和修正目標基本趨于穩定。修正前，參數最大誤差為66.7%，修正后參數最大誤差仍有-10.1%。但是特征值實部在修正前最大誤差為-41.07%，修正后最大誤差為0.95%；特征值虛部在修正前最大誤差為16.55%，修正后最大誤差為1.15%。從修正結果可以看出，考慮模型形式誤差后，軸承-轉子系統的模型修正參數雖然仍存在比較大的誤差，但是目標特征值誤差已經修正到工程可接受的范圍內。

3 不平衡響應確認

為了對修正結果進一步驗證，采用不平衡響應的預測對修正后模型進行確認。不平衡響應仍然采用有限元軟件Nastran進行計算。考慮輪盤存在4.0×10-4kg·m的不平衡質量，工作轉速從1 Hz變化到150 Hz。圖6分別對初始模型、目標模型和修正后模型的不平衡響應預測結果進行了比較。

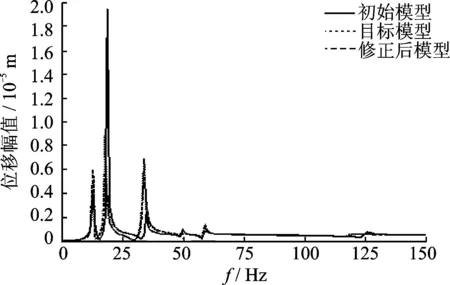
圖6 不平衡響應的比較Fig.6 The comparison of unbalance response

從圖6不平衡響應的比較中可以看出，修正前模型的不平衡響應不管是共振頻率位置還是共振峰值大小，與目標模型都有很大差別；而修正后模型的不平衡響應與目標模型基本重合。由此進一步驗證了考慮模型形式誤差的軸承-轉子系統動力學模型修正方法的穩健性和有效性。

4 結束語

考慮模型形式誤差，將工作轉速下的渦動頻率和阻尼參數作為殘差，可以有效地對軸承-轉子系統動力學模型進行修正，不平衡響應的確認也驗證了修正方法的有效性和穩健性。在系統恒定工作轉速下，該方法可以同時對軸承支承剛度、阻尼以及轉動慣量等非對稱的耦合參數進行修正。考慮模型形式誤差后，所識別得到的軸承支承參數仍有比較大的誤差，這對工程旋轉機械是非常有參考價值的。另外，所提出的方法需要使用實驗數據的修正進一步驗證。

[1] Goge D. Automatic updating of large aircraft models using experimental data from ground vibration testing[J]. Aerospace Science and Technology, 2003, 7(1): 33-45.

[2] 廖明夫, 譚大力, 耿建明, 等. 航空發動機高壓轉子的結構動力學設計方法[J]. 航空動力學報, 2014, 29(7): 1505-1519.

Liao Mingfu, Tan Dali, Geng Jianming, et al. Structure dynamics design method of aero-engine high pressure rotor[J]. Journal of Aerospace Power, 2014, 29 (7)：1505-1519. (in Chinese)

[3] Mottershead J E, Link M, Friswell M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296.

[4] 張保強, 陳國平, 郭勤濤. 使用有效模態質量和遺傳算法的有限元模型修正[J]. 振動、測試與診斷, 2012, 32(4): 577-580.

Zhang Baoqiang, Chen Guoping, Guo Qintao. The finite element model updating using effective modal mass and genetic algorithm[J].Journal of Vibration, Measurement & Diagnosis，2012, 32(4): 577-580. (in Chinese)

[5] 常濤, 郭勤濤, 張保強. 應用模型修正方法的印制電路板參數識別[J]. 振動、測試與診斷, 2013, 33(3): 509-513.

Chang Tao, Guo Qintao, Zhang Baoqiang. Parameter identification of printed circuit board using model correction method[J]. Journal of Vibration, Measurement & Diagnosis,2013, 33(3): 509-513. (in Chinese)

[6] Cortés F, Elejabarrieta M J. Computational methods for complex eigenproblems in finite element analysis of structural systems with viscoelastic damping treatments[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(44): 6448-6462.

[7] Elbeheiry E M. On eigenproblem solution of damped vibrations associated with gyroscopic moments[J]. Journal of Sound and Vibration, 2009, 320(3): 691-704.

[8] Arora V, Singh S P, Kundra T K. Damped model updating using complex updating parameters[J]. Journal of Sound and Vibration, 2009, 320(1): 438-451.

[9] 馮文賢，陳新．基于試驗復模態參數的有限元模型修正[J]．航空學報，1999，20(1)：11-16．

Feng Wenxian, Chen Xin. Updating design parameters of finite element model by using test complex modal data [J] .Acta Aeronautica et Astronautica Sinica, 1999, 20(1) : 11-16. (in Chinese)

[10]Lu Yong, Yu Zhenguo. A two-level neural network approach for dynamic FE model updating including damping[J]. Journal of Sound and Vibration, 2004, 275(3): 931-952.

[11]蔣家尚，袁永新．基于復模態試驗數據的粘性阻尼矩陣的修正[J]．振動與沖擊，2007, 26(5):74-80．

Jiang Jiashang, Yuan Yongxin.Vicious damping matrix updating from complex modal testing[J]. Journal of Vibration and Shock, 2007, 26(5): 74-80. (in Chinese)

[12]Datta B N, Deng S, Sokolov V O, et al. An optimization technique for damped model updating with measured data satisfying quadratic orthogonality constraint[J]. Mechanical Systems and Signal Processing, 2009, 23(6): 1759-1772.

[13]Yuan Yongxin, Guo Yongqiang. A direct updating method for damped gyroscopic systems using measured modal data[J]. Applied Mathematical Modelling, 2010, 34(6): 1450-1457.

[14]趙斌, 陳果. 轉子-支承耦合結構的模型修正研究[J]. 航空計算技術, 2014, 44(5): 86-91.

Zhao Bin, Chen Guo. Study on model updating of a rotor-support coupling structure[J]. Aeronautical Computing Technique, 2014, 44(5): 86-91. (in Chinese)

[15]Miao Hui, Zang Chaoping, Friswell M. Model updating and validation of a dual-rotor system[C]∥Proceedings of the 26th International Conference on Noise and Vibration Engineering (ISMA2014). Leuven, Belgium: Catholic University of Louvain,2014: 2723-2738.

[16]張保強, 郭勤濤, 陳國平, 等. 基于復模態模型修正方法的磁懸浮軸承支承參數識別[J]. 南京航空航天大學學報, 2010, 42(6): 748-752.

Zhang Baoqiang, Guo Qintao, Chen Guoping, et al. Parameter identification of active magnetic bering support based on finite element model updating using complex modal data[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(6): 748-752. (in Chinese)

[17]Xu Yuanping, Zhou Jin, Di Long, et al. Active magnetic bearing rotor model updating using resonance and MAC error[J]. Shock and Vibration, 2015, 2015(2): 1-9.

[18]Chouksey M, Dutt J K, Modak S V. Model updating of rotors supported on journal bearings[J]. Mechanism and Machine Theory, 2014, 71(1): 52-63.

[19]Cavalini Jr A A, Lobato F S, Koroishi E H, et al. Model updating of a rotating machine using the self-adaptive differential evolution algorithm[J]. Inverse Problems in Science and Engineering, 2016, 24(3): 504-523.

[20]丁繼鋒, 馬興瑞, 韓增堯, 等. 結構動力學模型修正的三步策略及其實踐[J]. 航空學報, 2010, 31(3): 546-552.

Ding Jifeng, Ma Xingrui, Han Zengyao, et al. Three step model updating method in structure dynamics and its application[J]. Acta Aeronautica Et Astronautica Sinica, 2010, 31(3): 546-552. (in Chinese)

[21]Oberkampf W L, Helton J C, Joslyn C A, et al. Challenge problems: uncertainty in system response given uncertain parameters[J]. Reliability Engineering and System Safety, 2004, 85(1):11-19.

[22]Oberkampf W L, Roy C J. Verification and validation in scientific computing[M]. New York, USA: Cambridge University Press, 2010: 572-575.

[23]Adhikari S．Rates of change of eigenvalues and eigenvectors in damped dynamic system [J]. American Institute of Aeronautics and Astronautics Journal, 1999, 37 (11): 1452-1458.

[24]Chouchane M, Guedria N, Smaoui H. Eigensensitivity computation of asymmetric damped systems using an algebraic approach[J]. Mechanical Systems and Signal Processing, 2007, 21 (7):2761-2776.

*國家自然科學基金資助項目(51505398，U1530122，51275240)；航空科學基金資助項目(20150968003)

2016-03-17；

2016-06-17

10.16450/j.cnki.issn.1004-6801.2017.02.026

V231； O327； TH113

張保強,男，1981年9月生，博士、助理教授。主要研究方向為復雜結構動力學模型修正和模型確認。曾發表《Static frame model validation with small samples solution using improved kernel density estimation and confidence level method》(《Chinese Journal of Aeronautics》2012,Vol.25,No.6)等論文。 E-mail: bqzhang@xmu.edu.cn