壽命服從兩參數對數Laplace分布的統計分析方法研究

徐曉嶺， 顧蓓青，王蓉華

(1.上海對外經貿大學 統計與信息學院，上海 201620； 2.上海師范大學 數理學院，上海 200234)

?

【基礎理論與應用研究】

壽命服從兩參數對數Laplace分布的統計分析方法研究

徐曉嶺1， 顧蓓青1，王蓉華2

(1.上海對外經貿大學 統計與信息學院，上海 201620； 2.上海師范大學 數理學院，上海 200234)

首先提出了一種新的壽命分布——兩參數對數Laplace分布，研究該分布的密度函數、失效率函數的圖像特征以及數字特征，其次在全樣本、定數截尾樣本以及缺失數據場合下，分別研究了位置參數、刻度參數的點估計與區間估計問題，為滿足實際工作者的需要，列出了與樞軸量對應的分位數表，最后通過一個實例說明方法的應用。

兩參數對數Laplace分布；全樣本；定數截尾樣本；缺失數據；點估計；區間估計

稱某產品的壽命T服從兩參數對數Laplace分布LNL(μ,β)，記為T～LNL(μ,β)，其分布函數FT(t)和密度函數fT(t)分別為

其中，-∞<μ<+∞稱為位置參數， β>0稱為刻度參數。

若令X=lnT，則X服從位置參數μ、刻度參數β的兩參數對稱Laplace分布，記為X～L(μ,β)，其分布函數FX(x)和密度函數fX(x)分別為

特別地，當取μ=0，此時稱X服從單參數Laplace分布，記為X～L(β)；而若取μ=0,β=1，此時X～L(1)，稱X服從標準Laplace分布。

兩參數對稱Laplace分布由于它與正態分布相比具有尖峰厚尾的特性而使得它在工程科學、質量控制、環境科學以金融等領域得到了廣泛的應用。鑒于兩參數對數Laplace分布與兩參數對稱Laplace分布的對數關系，所以關于兩參數對數Laplace分布的統計分析可以通過分析兩參數對稱Laplace分布來實現。關于兩參數對稱Laplace分布的統計分析及應用已有許多文獻作了較為深入的研究。Pedro Puig和Michael A.Stephens在文獻[1]中通過4個實例研究了兩參數對稱Laplace分布的擬合檢驗問題。王振杰等[2]推導了兩參數對稱Laplace分布總體中位數的概率密度函數，證明了位置參數的極大似然估計是無偏的。唐林俊等[3]通過對深滬兩地股票市場的股指收益率數據進行分析，發現兩地股票收益率分布均呈“尖峰厚尾”的特性，為此引入兩參數對稱Laplace分布代替過去人們常用的正態分布去刻畫收益率分布，結果顯示Laplace分布比正態分布擬合效率有了明顯的提高。杜紅軍等[4]采用兩參數對稱Laplace分布來刻畫尖峰厚尾性，給出了金融資產的VaR和CVaR風險的計算和估計。王炳章[5]證明了兩參數對稱Laplace分布(原文獻稱其為對稱指數分布)位置參數的極大似然估計為樣本中位數，并證明了位置參數的極大似然估計具有無偏性與強相合性，同時還證明了刻度參數的估計也具有強相合性。徐美萍等[6]研究單參數Laplace分布的貝葉斯點估計，并用上證指數收益率數據作了實證分析。張永芳等[7]根據金融資產收益率的實際分布具有尖峰厚尾特性，引入兩參數對稱Laplace分布，得到了風險價值VaR和條件風險價值CVaR的計算公式，并采用滬深股市的股票進行了實證研究。趙志文等[8]研究兩個單參數Laplace分布總體在數據有部分缺失的情形下參數的估計及相關假設檢驗問題。就目前關于兩參數對稱Laplace分布的統計分析而言大都涉及參數的點估計(包括極大似然估計與貝葉斯估計等)，而參數的區間估計的研究卻很少涉及。

1 兩參數對數Laplace分布的特征性質

利用高等數學的知識容易得到如下關于兩參數對數Laplace分布密度函數、失效率函數的圖像特征以及數字特征：

定理：設某產品的壽命T服從兩參數對數Laplace分布，T～LNL(μ,β)，則T有如下特征性質：

2) 失效率函數λT(t)的圖像特征為：當β<1時，λT(t)在t∈(0,eμ)上嚴格單調增加，在t∈[eμ,+∞)上嚴格單調下降；當β=1時，λT(t)在t∈(0,eμ)上嚴格單調增加，在t∈[eμ,+∞)上嚴格單調下降；當β>1時，λT(t)在t∈(0,eμ)上嚴格單調下降，后嚴格單調增加，在t∈[eμ,+∞)上嚴格單調下降。

2 兩參數對數Laplace分布全樣本場合下參數的點估計與區間估計

首先，分別給出單參數Laplace分布總體和兩參數對稱Laplace分布總體全樣本場合下參數的極大似然估計。

引理1：設總體X服從單參數Laplace分布，X～L(β)，X1,X2,…,Xn是來自總體X的容量為n的一個簡單隨機樣本，其次序統計量記為X(1),X(2),…,X(n)，則參數β的極大似然估計為

引理2：設X1,X2,…,Xn是來自總體X服從兩參數對稱Laplace分布L(μ,β)的一個容量為n的簡單隨機樣本，其對應的樣本觀察值為x1,x2,…,xn，次序統計量記為X(1),X(2),…,X(n)，對應的次序觀察值為x(1),x(2),…,x(n)，則

2) 刻度參數β的極大似然估計為：

2.1 位置參數μ的區間估計

于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

由此，給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為：

于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

由此，給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為

取樣本容量n=3(1)30，通過10 000次Monte-Carlo模擬得F(μ)的0.99，0.95，0.90，0.85，0.15，0.10，0.05，0.025，0.01的上側分位數，如表1所示。

2.2 刻度參數β的區間估計

又

于是T(β)是僅含有參數β的樞軸量，又T(β)是β的嚴格單調減函數。

給定顯著性水平α，樞軸量T(β)的上側1-α/2,α/2的分位數分別記為T1-α/2和Tα/2，參數β的置信水平1-α的區間估計為

取樣本容量n=3(1)30，通過10 000次Monte-Carlo模擬得T(β)的0.99，0.95，0.90，0.85，0.15，0.10，0.05，0.025，0.01的上側分位數，如表2所示。

2.3 模擬分析

給定置信水平1-α=0.90，取樣本容量n=5(5)30，參數真值取為μ=-5,0,5，β=0.5,1,2通過1 000次Monte-Carlo模擬得參數μ,β的區間估計的平均下限、平均上限和平均長度，同時統計1 000次模擬所得的區間估計包含參數真值的次數，結果如表3所示，其中k1,k2分別表示參數μ,β區間估計包含參數真值的次數。從中可以看到：

1) 固定參數真值，區間估計的長度隨樣本容量的增加而變小，即區間估計愈精確；

2)k1,k2的值大多在900以上，這也說明置信水平達到了0.90。

表1 樞軸量F(μ)的上側分位數

表2 樞軸量T(β)的上側分位數

續表(表2)

表3 兩參數對稱Laplace分布參數μ,β區間估計的1 000次模擬

續表(表3)

μβnμ的區間估計平均下限平均上限平均長度k1β的區間估計平均下限平均上限平均長度k200．51210-0．43030．33550．76599060．26431．16410．899791115-0．30360．27960．58329030．28371．04720．763490520-0．24690．26270．50969020．28980．96960．679990625-0．23970．22470．46459010．29390．91970．625890330-0．21730．21260．43009000．30040．91450．614291510-0．84390．66701．51089000．52992．33371．803789915-0．61150．57261．18419020．56602．08901．522990620-0．51140．51251．02409010．57401．92061．346690325-0．47650．44780．92439070．59261．85441．261789930-0．44130．41890．86029100．59841．82191．223591210-1．65081．33602．98688981．06644．69613．629689915-1．17451．15532．32989001．13274．18033．047689820-1．00701．04492．05199161．14473．83012．685490325-0．92350．91861．84219111．18293．70152．518590830-0．85780．85611．71399261．20723．67542．468291350．512104．58645．33800．75169000．25831．13760．8792909154．69515．28460．58959010．28141．03830．7570901204．74825．26430．51619070．28990．96990．6800907254．76235．22370．46149070．29320．91750．6243910304．77485．20320．42849030．30060．91520．6146908104．14275．65771．51509130．52772．32361．7959917154．39245．58551．19319090．56402．08161．5176902204．50375．52991．02628990．58171．94651．3648899254．53095．45270．92189000．59081．84861．2578904304．57225．43110．85899000．60061．82851．2279911103．34456．38573．04129051．04854．61703．5685907153．79236．16932．37709121．10784．08852．9807903203．99376．01362．01999031．15913．87842．7193905254．06005．90031．84029001．18523．70852．5233900304．12155．83671．71519021．20913．68112．4720905

3 兩參數對數Laplace分布定數截尾場合下參數的點估計與區間估計

設總體T服從兩參數對數Laplace分布LNL(μ,β)，T(1),T(2),…,T(r)是來自總體T的容量為n的前r個次序統計量。

令X=lnT,X(i)=lnT(i),i=1,2,…,r，則X～L(μ,β)，而X(1),X(2),…,X(r)是來自總體X的容量為n的前r個次序統計量。

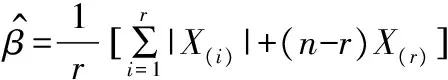
3.1 位置參數μ的點估計與區間估計

1) 當r≥[n/2]+1時，參數μ的點估計可取為

2) 當r<[n/2]+1時

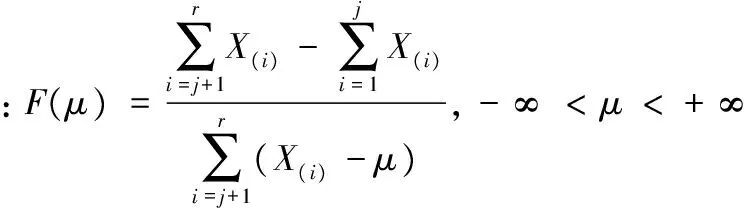
于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

則參數μ的點估計為

給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為：

值得指出的是上述所得到的參數μ的區間估計對r≥[n/2]+1也是成立的。

于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為

值得指出的是上述所得到的參數μ的區間估計對r≥[n/2]+1也是成立的。

3.2 刻度參數β的點估計與區間估計

2) 構造如下僅含有參數β的樞軸量：

又

于是T(β)是僅含有參數β的樞軸量，又T(β)是β的嚴格單調減函數。

則參數β的點估計為

給定顯著性水平α，樞軸量T(β)的上側1-α/2,α/2的分位數分別記為T1-α/2和Tα/2，參數λ的置信水平1-α的區間估計為

4 兩參數對數Laplace分布數據缺失場合下參數的點估計與區間估計

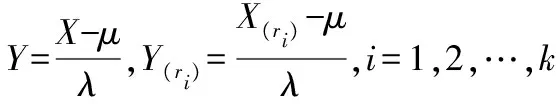
4.1 位置參數μ的點估計與區間估計

于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

則參數μ的點估計為

給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為

于是F(μ)是僅含有參數μ的樞軸量，又F(μ)為μ的嚴格單調增函數，且

則參數μ的點估計為

給定顯著性水平α，樞軸量F(μ)的上側1-α/2,α/2的分位數記為F1-α/2和Fα/2，易見參數μ的置信水平1-α的區間估計為

4.2 刻度參數β的點估計與區間估計

又

于是T(β)是僅含有參數β的樞軸量，又T(β)是β的嚴格單調減函數。

則參數β的點估計為

給定顯著性水平α，樞軸量T(β)的上側1-α/2,α/2的分位數分別記為T1-α/2和Tα/2，參數β的置信水平1-α的區間估計為

5 實例分析

下面通過文獻[1]中所涉及的兩個服從兩參數對稱Laplace分布X～L(μ,β)的實例數據說明本文方法的應用。

文獻[1]提供的100個紗線斷裂強度數據，從小到大排序為：62,66,78,79,80,84,84,85,85,86,86,87,88,88,89,89,91,91,91,91,92,92,92,92,93,94,94,94,95,95,95,96,96,96,96,96,97,97,97,97,97,97,98,98,98,98,98,98,98,99,99,99,99,99,100,100,100,100,100,101,101,101,101,102,102,102,102,102,102,102,103,103,103,103,104,104,104,104,104,104,105,105,106,107,107,109,110,111,111,111,111,114,115,117,122,132,132,137,137,138。

1) 在全樣本場合下，易見參數的極大似然估計為

利用本文方法，通過Monte-Carlo模擬當n=100時樞軸量F(μ)的上側0.975,0.95,0.05,0.025分位數分別為：1.558 69,1.618 75,2.606 81,2.776 97，樞軸量T(β)的上側0.975,0.95,0.05,0.025分位數分別為：272.172,291.44,679.648,758.688。于是可得參數μ的置信水平0.90,0.95的區間估計分別為：(97.460 5,101.357)和(97.064 4,101.748)，而參數β的置信水平0.90,0.95的區間估計分別為：(5.505 79,12.839 7)和(4.932 2,13.748 7)

作為比較，參數μ的點估計也可取為：

作為比較，參數β的點估計也可取為

若給定置信水平0.90，0.95，則可知參數μ的區間估計分別為：(97.036 2,100.316)和(96.692 6,100.622)，而參數β的區間估計分別為：(5.380 38,12.810 3)和(4.900 16,13.601 7)。

若給定置信水平0.90，0.95，則可知參數μ的區間估計分別為：(95.578 5,103.293)和(95.122,104.428)，而參數β的區間估計分別為：(5.001 05,14.804 3)和(4.428 14,16.066 2)。

4) 若這100個數據僅保留15個數據：x(1),x(2),x(3),x(4),x(5),x(12),x(25),x(83),x(86),x(87),x(92),x(93),x(94),x(95),x(100)，此時r1=1,r2=2,r3=3,r4=4,r5=5,r6=12,r7=25,r8=83,r9=86,r10=87,r11=92,r12=93,r13=94,r15=100，而k=15,j=8。

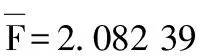
參數μ的點估計為：

參數β的點估計為：

若給定置信水平0.90，0.95，則可知參數μ的區間估計分別為：(95.527 7,103.028)和(94.796 2,103.713)，而參數β的區間估計分別為：(6.173 08,11.654 7)和(5.737 09,12.277 9)。

[1] PEDRO P,MICHAEL A S.Tests of Fit for the Laplace Distribution with Applications[J].Technometrics,2000,42(4):417-424.

[2] 王振杰，歐吉坤，曲國慶.一元Laplace分布的L1-范估計的無偏性[J].武漢大學學報(信息科學版)，2001,26(4):361-363.

[3] 唐林俊，楊虎.深滬股市收益率分布特征的統計分析[J].數理統計與管理，2004,23(5):1-4.

[4] 杜紅軍，劉小茂.拉普拉斯分布下的VaR和CVaR風險計算[J].應用數學，2006(S):225-228.

[5] 王炳章.對稱指數分布的參數估計及其優良性[J].煙臺大學學報，2007,20(4):250-253.

[6] 徐美萍，段景輝.Laplace分布參數估計的損失函數和風險函數的Bayes推斷[J].統計與決策，2010(1)：13-14.

[7] 張永芳，張全元.基于Laplace分布和CVaR的投資組合模型研究[J].重慶工商大學學報，2014,31(4):1-7.

[8] 趙志文，劉洋萍，于薇.具有部分缺失數據的兩個拉普拉斯分布總體參數的估計與檢驗[J].吉林師范大學學報，2015(3):61-64.

[9] BAIN L J,ENGLEHART M.Interval Estimation for the Two Parameter Double Exponential Distribution[J].Technometrics,1973,15:875-887.

(責任編輯 唐定國)

Statistical Analysis Method Study of the Life with Two-Parameter Logarithmic Laplace Distribution

XU Xiao-ling1, GU Bei-qing1, WANG Rong-hua2

(1.School of Statistics and Information, Shanghai University of International Businessand Economics, Shanghai 201620, China; 2.College of Mathematics and Physics,Shanghai Normal University, Shanghai 200234, China)

A new life distribution called two-parameter logarithmic Laplace distribution was proposed. The image characteristics of density function and failure rate function as well as the numerical characteristics were studied for this distribution. Then the point estimates and interval estimates of location parameter and scale parameter were respectively researched under complete sample, type-I censored sample and missing data. To meet the needs of practitioners, we listed parts of quantile tables of pivotal quantity. Finally, one example was illustrated for the application of methods.

two-parameter logarithmic Laplace distribution; complete sample; type-I censored sample; missing data; point estimate; interval estimate

2016-11-23；

2016-12-25

國家自然科學基金資助項目(11671264)

徐曉嶺 (1965—)，男，博士，教授，主要從事可靠性統計研究。

10.11809/scbgxb2017.04.036

徐曉嶺， 顧蓓青，王蓉華.壽命服從兩參數對數Laplace分布的統計分析方法研究[J].兵器裝備工程學報，2017(4):169-178.

format:XU Xiao-ling, GU Bei-qing, WANG Rong-hua.Statistical Analysis Method Study of the Life with Two-Parameter Logarithmic Laplace Distribution[J].Journal of Ordnance Equipment Engineering,2017(4):169-178.

O213

A

2096-2304(2017)04-0169-10