提升學生數學思維能力
——《數表中的數學問題》教學反思

舒愛武

【教學過程】

一、觀察數表 發現規律

師：仔細觀察這個數表，這些數是怎么排列的？你發現了哪些規律？

（板書：發現規律）

生：2、4、6、8、10……都是雙數，其他的都是單數。

生：都是連續的自然數，橫著看，每個數都比前面一個數多1。

師：說明相鄰的數相差幾？

生：1。

生：豎著看，相鄰的上下兩個數相差8，因為有8列。

師：同學們很認真，發現了許多規律，這張數表中肯定會有更多的規律。今天我們就來探討數表中的數學問題。

（板書課題）

二、提出問題 解決問題

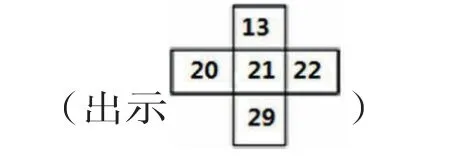
（如圖：在數表中畫上這樣一個十字框）

師：你能提出哪些數學問題？

生：這五個數的和是多少？

生：這個框中，橫著的三個數和是多少？豎著的三個數的和是多少？

生：你發現了什么規律？

生：這5個數的平均數是多少？

師：對啦！還有沒有思維更開闊一些的？

生：這五個數有什么關系？

師：這個問題非常好！數學就是研究數與數之間關系的學科。

師：現在提出了問題，那接下來該干什么？

生：解答問題。

（板書：解決問題）

師：我們先來解決“5個數的和是多少？”把方法用算式寫在作業紙上。

師：老師把你們的方法抄在黑板上，還有不同的方法嗎？

（板書：①2＋9＋10＋11＋18）②（2＋18）＋（9＋11）＋10③20×2+10 ④30×2－10）

師：還有不同的方法嗎？

生：10×5＝50。

（板書⑤10×5＝50）

師：看著這個算式，有沒有疑問？上面只有一個10？

生：把11拿一個給9，就是3個10，然后從18拿8到2這里也就是5個10。

師：這種方法可以取個什么名字？

生：移多補少。

（板書：移多補少）

師：還有方法嗎？

生：我把中間那個數看作a，它左面的數就是a-1，右邊的數是a+1，上面的數是a-8，下面的數是a+8，一共是5a，就是5乘10等于50。

（板書：a+a-1+a+1+a-8+a+8＝5a）

師：這位同學講得非常清楚，剛好解釋了第五種方法，為什么可以用10×5來求五個數的和。

師：我們會求這五個數的和了。你能提出類似的問題嗎？

生：框出的5個數是5、12、13、14、21，這五個數的和是多少？

師：剛才同學的提問，是告訴大家框中的五個數分別是多少，其實，你用不著每個數都告訴，就能求出五數的和。

師：你會選擇告訴大家哪一個數就能求出來？

生：中間數是13，五個數和是多少？

生：13×5=65。

師：5個13哪里來的？

生：14移 1給 12，21移 8個給5，得到5個13。

師：你發現了什么？

生：中間數就是平均數。

師：所有的中間數都是它們的平均數嗎？

生：這個數在這個表中是對的。不同的數表就不一定了。

師：如果框的形狀也不同，就要觀察研究后再確定。

師：中間數是13，這個數在表中看得到。你還能大膽地提出類似問題嗎？

師：如果中間數是a，和是多少？

生：a×5＝5a。

師：中間數是★，和是多少？

生：★×5＝5★。

師：我們怎樣求5個數的和？

生：中間數×5。

（板書：中間數×5＝和）

師：非常好。剛才告訴5個數，求它們的和是多少？是順向的問題。那我們也可以提出逆向的問題嗎？你來試試。

生：如果5個數的和是145，這五個數是多少？

師：誰來分享一下，你是怎么思考的？

生：（黑板上邊板書邊講）先求中間數145÷5＝29，再左邊少1是28，右邊多1是30，上邊減8是21，下邊加8是37。

師：為什么只要求出中間數，就能通過加減來求出周圍的數？

生：左右相差1，上下相差8。

師：想不想再挑戰一下，數字變大了，和是160，這五個數是多少？

生：中間數是160÷5＝32，左邊是 31，右邊 33，上邊24，下邊 40。

師：講得非常完整。你們都是這樣的嗎？（學生齊答“是”）

師：只有一位同學說“不是”，你說說為什么？

生：32 后面沒有 33，33 在下面一行了。這個表格中框不出這樣的五個數。

師：想到什么問題了呢？

生：如果32的右邊是33的話，就要9列。那么它們的上下就不是相差8了，是相差9了。

師：所以呢？

生：這個問題不成立。

師：是的，這張數表中不能框出這5個數。因為32不能作中間數。還有哪些數不能作中間數呢？

生：第一行。

師：還有嗎？

生：還有第一列，第八列。

師：怎樣用數學語言清晰地表達？

生：小于等于8的數和8的倍數都不能作中間數。

（板書：≤8）

師：8的倍數除以8，余數都是幾？

生：0。

（板書：（）÷8 余0）

生：第一列的所有數除以8余數是1。

（板書：（）÷8 余1）

師：這道題目還引發我們思考：在這個數表中，和是160的5個數是框不出來的。哪5個數的和最接近160呢？

生：把框向左平移一格，和是 155，少了 5。

師：為什么是少5？

生：向左平移一格，每個數都少了1，共少了5。

師：還有不同的解釋嗎？

生：原來中間數當作32×5＝160，向左平移一格后，中間數變成 31，31×5＝155。

師：如果把下面這個框平移一格，那么5個數的和會發生什么變化？

（出示一個把5個數都遮住的十字框）

生：可能有四種情況：向右平移一格，每個數增加1，和增加5；向左平移一格，每個數少1，和減少5；向下平移一格，每個數增加8，和增加8×5=40；向上平移一格，每個數減少8，和減少8×5＝40。

師：你會提出相關的數學問題，讓同學解答嗎？

生：把這個框向下平移1格，中間數是幾？

師：能不能再大膽一點，提出表格中沒寫出的數呢？

生：把這個框向下平移10格，中間數是幾？

生：21+8×10＝101。

師：這是一個方向平移的問題，能提出兩個方向都平移的問題嗎？

生：這個框，先向右平移2格，再向下平移5格，五個數分別是多少？

師：要知道5個數分別是多少，只要知道中間數就能推出，那我們就看誰先求出中間數。

生：向右平移2格要加上1×2，再加上向下平移5格，增加的是 5×8＝40，結果是21+2+40＝63。

（板書：21+1×2+8×5＝63）

師：大家非常迅速就解答了，那會不會提出雙向的又是逆向的問題呢？

生：框中5個數的和是235，這5個數與下面框相比，向下、向右各平移了多少格？

師：說說你的思路，我們可以課后再去計算。

生：先求出5個數的中間數。再看比10多了幾個8，就是向下平移幾格；多出幾，就是再向右平移幾格。

師：同學們的表現真是太棒了！如果不斷地研究下去，還會發現數表中更多的數學問題。

三、回顧總結 反思方法

師：今天學習數學的方法是什么？我們有什么新收獲？

生：我們發現了數表中的規律。我們會求框出的5個數的和是多少。

生：我們先觀察發現規律，提出問題，再尋找方法來解決問題，在解決問題的過程中又發現新的規律。

師：總結得非常好。其實如果數表排列變了，框的形狀變了，我們都可以用這種方法進行學習。我特別欣賞大家能自己提出問題，分析問題，并想辦法解決問題，又在解決問題的過程中不斷地發現新的問題。數學家研究問題就是經歷了這樣的過程，一些科學研究也是這樣的經歷。同學們這種自主學習的狀態非常棒！

【課后反思】

一、提問，培養學生的問題意識

本節課從頭至尾讓學生發現規律，從中提出問題。出現數表后，嘗試提出問題“框出的五個數的和是多少？”“這五個數有什么關系？”當學生解決了問題，再引導“你能提出類似的問題嗎？”。指導提出問題的方法，剛才我們提的問題都是順向的，也可以反向提問；剛才我們是單向提的問題，也可以雙向提問……一節課，讓學生不斷地提出問題，解決問題，在解決問題的過程中又提出問題。課堂中舍得花這么多時間讓學生去提問題，因為提出一個問題比解決一個問題更重要，前者需要有創造性的想象，而后者也許僅僅是一個技能。

二、提問，提升學生的思維能力

通過在解決問題的過程中不斷的提問，滲透培養學生的洞察能力，模型思想及不斷推測其他的結果等。關注學生思維的品質，如思維的敏捷，看到數表中上下相差8，馬上想到“每列都一樣嗎？”“中間數就是平均數嗎？”還有思維的深度，當讓學生求和是160的五個數是多少？而數表中不能框出這5個數時，激起學生的質疑，為什么不行呢？怎樣的數不能作中間數呢？一步步引入深層次的思考，讓學生經歷問題研究的過程。取得階段性的成果，前進中又遇到一些問題，并想辦法解決這些問題。數學家研究問題就是經歷了這樣的過程，一些科學研究也是這樣的經歷。

三、提問，關注知識間的聯系與運用

在整個探究過程中，運算能力、空間觀念、模型思想，融合運用。“5個10的和是多少？”學生展示3種方法，后面又補充了兩種方法，共有5種方法。就求出結果來說，這些方法是沒有好壞之分的，無非就是效率的問題。但是作為教育任務的數學，好的方法聯系到數感、運算能力、模型思想，因此需要花時間去討論這些好的方法。“哪些數不能作中間數？”學生開始主要是根據空間位置來判斷的，回答是第一行、第一列、最后一列。引導學生用數學語言描述，就出現了小于8的數、8的倍數，除以8余數是0，除以8余數是1。“怎樣的5個數和最接近160？”“平移后，五個數和會發生什么變化？”引導學生思維進行空間的轉化——平移，運算與空間有機結合。