“動手做”：豐盈學生思維

陸 敏

蘇教版新教材設置“動手做”欄目，目的在于培養學生動手實踐的能力。“動手做”是基于數學活動經驗的“數學”本質和“經驗”屬性，要求學生在動手做的活動中學會思考、學會猜想、學會探究、學會歸納，著力于引導學生在活動中深化對數學知識和探究問題方法的掌握，組織對活動過程進行交流和反思。同時也體驗數學對適應未來社會和進一步發展的需要，增進對數學的理解，體驗數學和學習數學的價值。

一、導航圖例

1.“動手做”實施內容。

蘇教版新教材三年級下冊第50頁。

在制作的月歷上進行框數游戲。

2.“動手做”實施目的。

用長方形框在學生制作的月歷上每次框出3個數、4個數或多個數，研究每次框出的數之間的關系，算出每次框出的數的和。這些活動能培養學生探索規律的興趣與能力，能發展學生的思維。

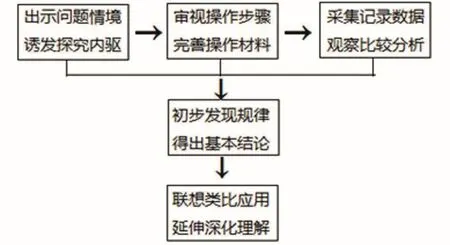
3.“動手做”實施流程。

二、導學路徑

1.出示問題情境，誘發探究內驅。

師：課件出示爺爺每天要吃一片VE，一盒有30片，夠吃一個月嗎？

生：有可能夠，有可能不夠。

師：這是怎么回事？請你說說什么時候夠？什么時候不夠？

生：有的月是30天，有的月是31天。

生：還有可能是28天或29天。

師：一個月中有30天的、31天的，平年的二月是28天，閏年就是29天。

師：日歷表中的天數有的一樣，有的不一樣，但是它們是日期與星期幾對應而排列的——我們稱它為七列數表，中間還隱藏著數與數之間的許多秘密，那七列數表中間到底隱藏著數與數之間哪些秘密呢？想不想知道？

2.審視操作步驟，初步發現規律。

師：利用下表1制作今年一月的月歷。有什么問題嗎？

表1

（學生制作月歷）

（1）每次框出同一行的3個數。

（學生活動、匯報）

師：誰來把你的發現與大家共享一下？

生：我框了6、7、8三個數，三個數相加的和是21，我發現中間的一個數乘3就得到21。我又框了11、12、13，三個數相加的和是36，我發現中間的一個數乘3就得到36。

師：會動腦筋的好學生。誰再來？

生：我框的是4、5、6三個數，三個數相加的和是15，我發現中間的一個數乘3就得到15。我還框了18、19、20三個數，三個數相加的和是57，我發現中間的一個數乘3就得到57。

生：我框的是28、29、30三個數，三個數相加的和是87，我發現中間的一個數乘3就得到87。

師：對上面這些同學的發現，誰能用一句話概括一下？

生：框出連在一起的三個數，中間的一個數乘3就是這三個數的和。

師：誰還有補充的？

生：我認為要加一個條件“在同一行中”。

師：誰再完整地說一說？

生：在同一行中，框出連在一起的三個數，中間的一個數乘3就是這三個數的和。

師：在同一行中，框出連在一起的三個數，還有神奇的規律，想知道嗎？

（學生活動、匯報）

師：誰來把你的發現與大家共享一下？

生：我框了3、4、5三個數，前后兩個數相加的和是8，我發現中間的一個數乘2就得到8。我又框了13、14、15，前后兩個數相加的和是 28，我發現中間的一個數乘2就得到28。

師：會動腦筋的好學生。誰再來？

生：我框的是5、6、7三個數，前后兩個數相加的和是12，我發現中間的一個數乘2就得到12。我還框了21、22、23三個數，前后兩個數相加的和是44，我發現中間的一個數乘2就得到44。

生：我框的是24、25、26三個數，前后兩個數相加的和是50，我發現中間的一個數乘2就得到50。

師：對上面這些同學的發現，誰能用一句話概括一下？

生：在同一行中框出連在一起的三個數，中間的一個數乘2就是前后兩個數相加的和。

（2）每次框出同一列的3個數。

（學生活動、匯報）

生：我發現在同一列中，框出連在一起的三個數，中間的一個數乘3就是這三個數的和。

（學生活動、匯報）

生：在同一列中框出連在一起的三個數，中間的一個數乘2就是這前后兩個數相加的和。

小結：無論是在同一行中框出連在一起的三個數，還是同一列中框出連在一起的三個數，中間的一個數乘3就是這三個數的和；中間的一個數乘2就是這前后兩個數相加的和。

（3）每次框出同一行連在一起的4個數。

師：還想繼續探索嗎？

生：想。

師：你們想探索什么？

生：框出連在一起的四個數，是不是也有這樣的規律？

生：五個數呢？

師：提出的問題很好，很有價值。我們先來研究框出連在一起的四個數看看有什么規律？

（學生探索，匯報）

生：我們發現：兩端的兩個數相加的和等于中間的兩個數相加的和。舉個例子，6、7、8、9,6+9=15,7+8=15。

師：有沒有不同意見？

生：我還發現四個數的和，可以把這些數連加，也可以先把中間兩個數相加，再乘2等于這四個數的和。

師：同學們真棒！發現了兩個規律。下面我們再來動手框一框同一列的四個數。

（學生活動、匯報）

師：誰來說一說發現了什么？

生：在同一列的四個數，如，4、11、18、25，兩端的兩個數相加的和等于中間的兩個數相加的和。

生：我還發現四個數的和，可以把這些數連加，也可以先把中間兩個數相加，再乘2等于這四個數的和。

師：四個數的組成還有一種情況，誰猜一猜？

生：我認為是這四個數：4、5、11、12。

師：你是說分在兩行、兩列的4個數。

生：是的。

師：這四個數有什么規律呢？同桌研究一下。

（學生匯報）

生：也有上面的兩個規律。

師：實際上就是斜行上的兩個數相加的和相等（左上的數與右下的數相加的和等于左下的數與右上的數相加的和），四個數的和等于斜行上的兩個數相加的和乘2。

3.聯想類比應用，延伸深化理解。

師：其實在我們數學領域，日歷表是日期與星期幾對應而排列成的七列數表，我們還可以設計出多種列數不同的數表，因為數表是按一定的規律排列的，所以隱藏著很多數與數之間的關系。

每次框出更多個數，更多的數可能在同一行或同一列，也可能分在不同行、不同列。框出的數都會具有上面討論的關系與求和方法，根據上面的排列規律與求和經驗，課后可以進一步研究更多個數里的數學知識。

4.小結。（略）

三、教學思考

1.“動手做”讓學生主動參與。

在學習過程中，學生有思維活躍、思維遲鈍之分，如何讓全體學生動起來，對于思維遲鈍的學生，教師要給予及時的關注和幫助，鼓勵他們主動參與數學學習活動，并在大家的幫助下嘗試用自己的方式解決和探索問題，讓他們勇于發表自己的見解，對于他們在動手做的過程中出現的錯誤，要幫助他們分析產生困難或錯誤的原因，并鼓勵他們自己去認識、去領悟，從而培養他們的學習興趣。在教學中凡是讓學生探究、動手操作的內容，教師必須先做，做到心中有數。另外還要了解學生對要學習內容、知識的基礎掌握情況，讓學生參與自主學習、參與合作學習，師生一起動手做，輔導在動手做方面有困難的學生學習，通過教師與學生互動、學生與學生互動、合作交流、相輔相成的有效方式，引導學生學會歸納和反思，學會把自己做過的事情寫出來，幫助學生學會用語言表達，把自己對知識產生、發展過程說出來、說清楚,避免急于求成。

2.“動手做”讓學生體驗過程。

數學“動手做”活動是以問題為載體、以學生自覺參與學習為主的學習活動，教師通過探索問題的引領，讓學生全程參與動手做的過程，經歷相對完整知識的學習活動過程，它的核心是學生在教師的引導和幫助下有目標的、自主的“動手做”活動。

“動手做”活動是數學學習的一種手段，目的是更好地促進學生對數學知識的理解，能用數學的語言、符號進行表達和交流。“動手做”只能為學習者提供體驗學習的一個過程，學生學習數學體驗的認知主要是通過“動手做”活動，同時也是眼、手、腦等多種感官協調參與的學習活動，是鍛煉數學思維發展的內在動力。“動手做”活動就是要為學生創設一個猜想、探索、發現、類比、歸納的活動環境，使每個學生都能體驗和參與到探索數學知識的活動中去，最終達到學會知識、理解知識、運用知識的目的。

3.“動手做”促學生獨立思考。

《數學課程標準(2011年版)》把“數學思考”作為小學生數學學習的四大目標之一，并作了具體的闡述：經歷觀察、實驗、猜想、證明等數學活動過程，發展合情推理能力和初步的演繹推理能力，能有條理地、清晰地闡述自己的觀點。數學和思維是緊密聯系的，數學思維涉及很多的成分，其核心是邏輯思維，數學“動手做”活動是系統訓練學生數學思維的“操場”，通過生活中具體事例或古代著名數學問題，引導學生經歷猜測、驗證、觀察、分析等數學活動，進行簡單的有條理的數學思考，建立數學模型，逐步發展學生的歸納、類比、猜想與論證等各種數學思考的基本方法。在“動手做”活動中鼓勵學生獨立思考，采用諸如小組合作、實踐操作、實際調查、直接收集數據、真實數據計算等活動形式，使學生真正動起來，在“動手做”活動中積累活動經驗，提升數學能力和素養。

4.“動手做”促學生模型建構。

《數學課程標準（2011年版）》明確指出：“模型思想的建立是幫助學生體會和理解數學外部世界聯系的基本途徑。建立和求解模型的過程包括：從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示問題中數量關系和變化規律，求出結果，并討論結果的意義。這些內容的學習有助于學生初步形成模型思想，提高學習數學的興趣和應用意識。”“動手做”是讓學生經歷知識的形成與應用的過程，“動手做”活動是通過數學上的一些具體問題，讓學生通過觀察、猜想、探索、歸納、反思、架構模型的過程，在這個過程中有利于學生去發現、提出有價值的問題，有利于分析、解決問題，有利于發現規律、掌握技能，從而培養創新意識。