圍繞核心 精準設計
——特級教師王文森《一切皆有可能》教學賞析

徐偉平

“數量多，摸到的可能性就大；數量少，摸到的可能性就小；數量相等，摸到的可能性就相等”，這是多數教師對可能性大小教學的認識。但在實際中，可能性大小的出現卻帶有一定的隨機性。換句話說，有時候可能性的大小很難用實驗去驗證。那么“可能性”教學的核心是什么呢？筆者以為：一件事情發生的可能性大小，與數量有關，數量確定，可能性就確定了。可能性大小可以推理，可以計算，其教學的核心是發現并掌握可能性大小的規律。浙江省特級教師王文森《一切皆有可能》一課，緊緊圍繞核心，精準設計，讓學生在有趣、有味的活動中，掌握了可能性大小的知識。

【教學過程】

一、放球游戲

出示課件：

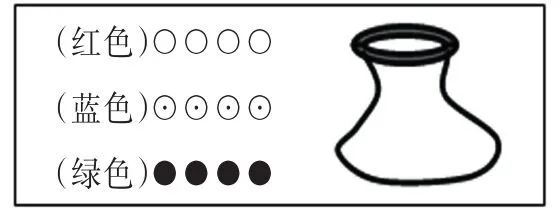
師：任意摸一個球，一定是紅球，怎么放？

生1：（黑板演示）

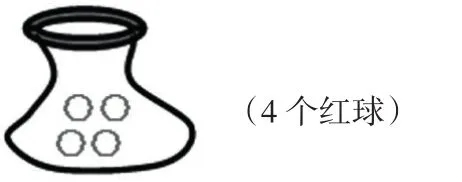
師：為什么這么放？

生2：一定是紅球，所以袋子里只能放紅球。

師：其他球可以放嗎？為什么？

生3：不可以，因為如果有其他顏色球的話，就不一定是紅球了。

師：還可以怎么放呢？

學生依次演示：

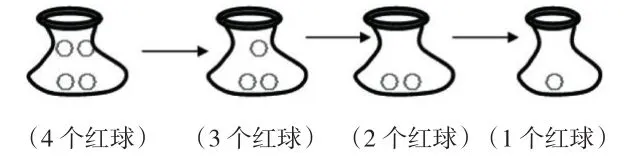
師：袋子里裝4個、3個、2個、1個都可以，誰能用一句話來概括一下“袋子里怎么放球，摸出來一定是紅球”？

生5：袋子里只能放紅球，其他球不能放。

生6：袋子里至少要放1個紅球，其他球不能放。

師：任意摸一個球，不可能是紅球，怎么放？

學生分別在黑板上擺放，教師整理：

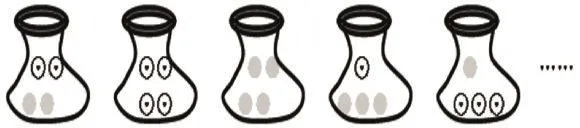
師：通過剛才操作，袋子里要怎么放，摸出來的球不可能是紅球？

生1：只要不放紅球，放其他顏色的球就可以了。

生2：只要不放紅球，其他顏色球的數量不限。

師：任意摸一個球，可能是紅球，怎么放？

學生分別在黑板上擺放，教師整理：

師：摸出來可能是紅球，袋子里應該怎么放？

生1：一定要有紅球，其他顏色球肯定也要有。

生2：紅球至少有1個，其他顏色球也至少要有1個。

4.師：（小結）剛才在放球的過程中，出現了哪幾種情況？

生：一定、可能、不可能（教師板書：一定、可能、不可能）

【思考之一：運用1個“袋子”、12個“小球”，通過“放球”、“分析”、“展示”、“概括”等環節的教學，讓學生深刻理解“一定”、“可能”和“不可能”事件的特性。教師以“放紅球”為情境，設置了“一定是紅球、可能是紅球和不可能是紅球，應該怎么放？”的三個精準問題，引導學生層層深入，通過對比，加深了理解。整個環節，學生不僅有直觀地感知，細致地思考，更有合理的結論，可謂別具匠心。】

二、猜球游戲

課件出示：

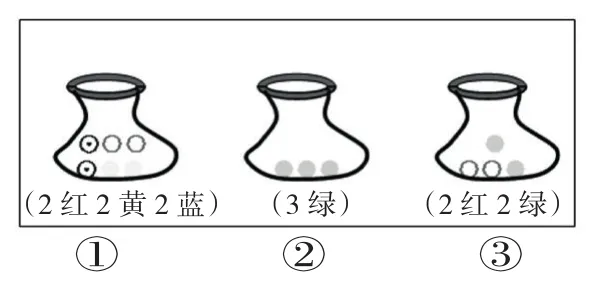
師：連續摸三次，結果是“●●●”（三個綠球），會是哪個袋子呢？（學生猜測）

師：可以排除哪個袋子？為什么？

生：可以排除①號，因為①號袋里沒有綠色球，不可能摸到綠色球。

1.去掉①號，留②③號。

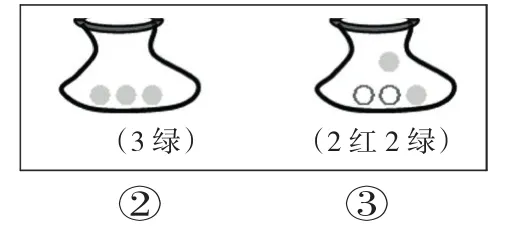
師：②號和③號袋子，你會選誰呢？為什么？

生：我們選②號，因為②號全部是綠球，摸出來一定是綠色的。

2.去掉②號，留③號。

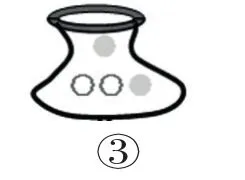
師：在③號袋中，如果第4次摸，可能是什么顏色的球？為什么？

生1：可能是綠球，也可能是紅色球。

生2：紅球和綠球的可能性一樣大。

……

【思考之二：“猜球”不是亂猜，它需要科學的依據，是一個思考、分析、判斷、推理的過程。教學中，學生根據“摸球”結果和三個袋子中不同顏色球的分布情況，先通過“淘汰”的方法確定不可能”的袋子（①號）；再通過分析對比”，選出可能性較大的袋子（②號）；最后，面對同樣具有可能性的袋子（③號）時，沒有點到即止，而是設置了“如果第4次摸，可能是什么球”的點睛之問。在學生尋找答案的同時，讓他們再次感受到：即使前面出現3次甚至更多次的同色球，也不能保證第4次或下一次一定是同色球，只要袋子里有幾種顏色球，結果就有幾種可能。】

三、摸球游戲

出示課件：

在本商場購買商品滿100元，可以摸一次球，摸到綠球可以得到精美禮品一份。

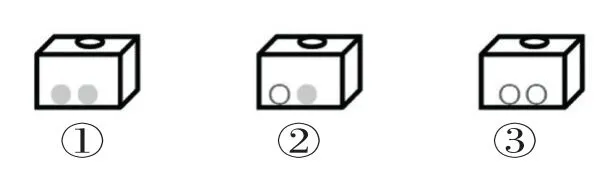
師：如果你是一位經理，你會選擇哪個盒子？為什么？

生1：我選②，因為摸到紅球和綠球的可能性一樣大，不能騙人。

師：你非常有誠信，那怎么才能公平呢？

生2：一人一半。

師：用什么數來表示②號盒子的可能性呢？

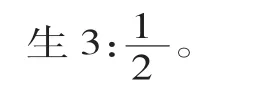
師：①號盒子摸到綠球的可能性是多少？

生4：因為只有綠球，所以一定能摸到綠球。

師：用什么數字來表示“一定”呢？

師：③號盒子摸到綠球的可能性是多少？用什么數字表示？

生6：③號盒子里沒有綠球，不可能摸到綠球，所以可能性是“0”。

師：為了能讓更多顧客摸到綠球，怎么辦呢？

生7：多放綠球（教師演示）：

3．師：如何才能降低摸到綠球的可能性？

學生展示：

師：它們的可能性又分別是多少？

【思考之三：“怎樣才能吸引更多顧客購買物品，但又不能造成商場虧損”，這是生活中常見的問題。教學時，在簡單分析三種可能性大小后，發現第2種是合理的，也是公平的；又通過“增加和減少可能性大小”的對比，讓學生感受到可能性大小隨數量變化而變化的規律，也不留痕跡地初步解決了“用數字可以表示可能性大小”的問題。】

四、賭博騙局

課件出示：

曾有一個擺攤摸球的人。當時圍觀的人們覺得很新鮮，有很多人參與摸球。他先擺了4個大小、形狀一樣的球，其中有2個紅色球，2個綠色球。當著觀眾的面，把所有4個球裝進一個普通的布袋中，慫恿大家來摸球。怎么個摸法呢？就是從這個裝有4個球的布袋中，任意摸出2個球，看看其中有幾個紅球，有幾個綠球。

獎：摸到“2個紅球”或“2個綠球”，獎勵5元；

罰：摸到“一個紅球和一個綠球”，罰5元。

師：對于這件事情，我們可以簡化為一個數學問題。

出示：

盒子里有2個紅球，2個綠球，一次任意摸出兩個球，可能出現哪些結果？

師：你覺得這位擺攤人最后“虧”了還是“賺”了？

（學生猜測）

師：其實一天下來，擺攤人“賺”了不少錢，你能找到原因嗎？

學生板演：

生1：

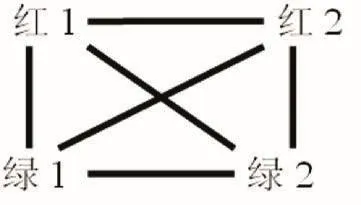
生2：

師：通過分析，一共有幾種可能？賺錢的有幾種可能？罰錢的又有幾種可能呢？

生1：一共有6種可能，其中賺錢的有4種，罰錢的有2種。

【思考之四：揭露“擺攤”騙局，再次把學生置于生活情境中，激發了學生的學習熱情。在表象中如何才能發現事物本質。學生們通過圖示、連線等數學化的語言，利用枚舉的方法將每種可能發生的情況一一列出。學生在分析各種可能發生的情形中，通過簡易的計算，輕而易舉地發現了問題，揭示了騙局的本質，領會了數學在生活中的應用。】

【感悟與啟示】

張奠宙教授指出：“可能性有大有小，主要靠理論分析，實驗為輔。摸球游戲，主要做思想實驗。迷信操作，是不正確的思維。”本節課很好地闡述了這一觀點。

1.教學過程精細。

本節課教學環節清晰、細致。“放球”讓學生感知事件發生的三種可能性；“猜球”讓學生了解到有幾種顏色球就有幾種可能性，誰的數量多誰的可能性就大；“摸球”讓學生明白可能性大小可以用數字來表示；“賭博騙局”則讓學生通過枚舉的辦法來計算可能性的大小。四個環節，由淺入深，易于理解。而更重要的是，教學中教師沒有讓學生通過具體的操作活動去驗證結果，而是別具一格地用圖形表示“袋子”，用不同顏色的磁鐵代替“小球”，這種設計簡單、直觀，讓學生在“非操作”中完成了“操作”的過程，思維性強，效果很好。

2.問題設計精準。

“問題是數學的心臟。”一節好課，精準的問題是關鍵。本節課，教師問題不多，但問得精準。“任意摸一個球，一定是紅球、不可能是紅球、可能是紅球，怎么放？”同樣的摸球，只要改變結果，就必然造成放球策略的改變，從而促使學生去思考，問得好。“連續摸三次，結果是三個綠球，會是哪個袋子呢？”引發了猜測，學生通過對比，逐步找到最合適的答案，問得準。“如果你是一位經理，你會選擇哪個盒子？為什么？”讓學生在選擇答案的同時，體會到可能性大小會隨著小球個數的變化而變化，問得巧。“你覺得這位擺攤人最后‘虧’了還是‘賺’了？”激發起探究的興趣，引發學生的思維，在自主選擇方法中揭示事件的本質，問得妙。

3.活動創設精妙。

有效的情境活動能激發學生的學習興趣。“放球”像一杯開水，平淡無奇，卻讓學生在操作與思考中感知了可能性；“猜球”像一杯飲料，色味俱全，學生在合理猜測、分步淘汰中理解了可能性大小的規律；“摸球”像是一杯濃茶，香中有澀，在對比分析中，學生掌握了用數字來表示可能性的方法；“賭博騙局”更像是一杯白酒，性烈甘甜，學生在挑戰中揭示了事物本質，學會了用數學的方法解決生活中的問題。四個情境四個游戲，既有簡單操作，更有猜測推理，學生在掌握可能性核心知識同時，增加了生活的體驗，進一步感受到數學來源于生活，應用于生活。