不同跨度地下洞室彈體侵徹效應數值模擬研究

劉紹鎏, 孫惠香, 王曉龍 ,張 悅, 黃文文, 康 婷, 張 璽

(1 空軍工程大學, 西安 710038; 2.94900部隊, 福建漳州 363000; 3 93199部隊, 哈爾濱 150001)

0 引言

第二次世界大戰以來,武器的威力和打擊精度迅速提高,精確制導武器在現代高技術戰爭中的地位日益凸顯,受到世界各國的高度重視。彈體侵徹一定深度后爆炸耦合入地的能量會大幅增加,破壞效應是觸地爆炸的數倍甚至數十倍,對地下目標構成嚴重威脅[1]。精確制導武器的侵徹爆炸效應已成為地下結構設計必須重點考慮的問題。

近年來,國內外學者對彈體的侵徹效應做了大量的研究,Gold[2]對高速彈體侵徹混凝土的侵徹阻力問題進行了數值模擬,并探討了不同材料模型對其侵徹響應結果的影響;Warren[3]等將空腔膨脹理論分析方法和數值模擬技術有機結合,采用復雜的混凝土本構模型理論對動態過程進行了分析;鄭文力等[4]對鉆地彈侵徹高強度混凝土靶進行了數值模擬研究,并對侵徹過程中裝藥的過載問題進行了分析;徐干成等[5]對地下洞室圍巖外加固抗炸彈侵徹性能進行了大量研究。然而,由于賦存環境的特殊性和侵徹效應的特點,地下洞室在彈體侵徹作用下的動力效應研究較少,所以文中對彈體侵徹作用下不同跨度地下洞室的受力情況和位移響應進行研究,為改進防護結構設計方法及促進防護技術發展提供理論依據。

1 數值模擬

ANSYS/LS-DYNA軟件是目前國際上著名的通用顯式動力學有限元分析軟件,能夠模擬各種復雜的結構計算問題,特別適合求解二維、三維非線性結構的高速碰撞、侵徹和爆炸沖擊等非線性動力學問題[6]。由于防護工程的特殊性,彈體侵徹危險性很大,會對結構造成嚴重的破壞,做原型試驗難度較大,所以文中應用ANSYS/LS-DYNA程序進行數值模擬研究。

1.1 數值模擬方案

彈體選用小直徑炸彈(SDB),該炸彈具有性能優異且方便攜帶的特點,特別適合現代的反恐作戰和近距離交火。現有SDB武器系統由GBU-39小直徑炸彈、載彈系統、任務規劃系統和后勤支援系統組成。包括彈架和4枚GBU-39/B炸彈在內,整套裝置重664 kg,長3.6 m、寬0.40 m、高0.40 m。GBU-39小直徑炸彈技術參數見表1。

表1 GBU-39技術參數

注:CRH為彈體頭部表面曲率半徑與彈體橫截面直徑之比。

文中選用1枚GBU-39/B炸彈對地下洞室進行垂直侵徹,侵徹點位于拱頂正上方,建模型時將其彈體視為均質實體,形狀為卵形彈頭。

地下洞室多為直墻拱結構,因此,數值模擬方案的結構形式為直墻拱結構,直墻部分高度為2 m,計算工況如表2所示[7]。

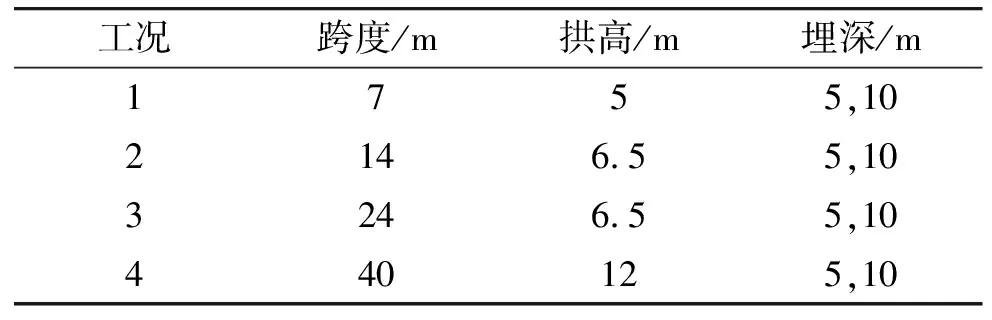
表2 數值模擬方案

1.2 材料模型

彈體選用MAT_JOHNSON_COOK材料模型,在考慮了應力、應變和溫度效應的同時,也能夠清晰地描述彈體在侵徹過程中的變形和受力特性。

巖石和混凝土拱形被覆結構均選用JOHNSON_HOLMQUIST_CONCRETE材料模型,該模型綜合考慮了大應變、高應變率、高壓效應,考慮了損傷及損傷積累,材料參數見文獻[8]。

1.3 算法選擇與計算模型

數值模擬采用Lagrange算法。為簡化起見,將巖體宏觀上看成連續、各向同性的均質體,不計實際上存在的裂隙影響。由于結構存在大跨度,洞室為細長型,長度方向取10 m、被覆結構兩邊各取5 m進行數值模擬。為節約計算時間和存儲空間,文中僅建立1/4模型,同時在對稱面上設置對稱面約束,并將無反射邊界條件實現于計算模型中[9]。在對洞室進行網格劃分時,對彈體與洞室侵徹接觸的區域網格進行加密,距離彈靶接觸區域較遠的地方網格劃分較稀疏。圖1為計算模型及網格劃分情況。

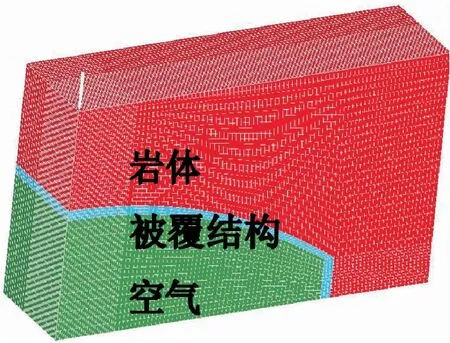
圖1 計算模型

2 數值模擬驗證

彈體侵徹巖體的機理十分復雜,長期以來此類問題的研究以試驗為基礎,并根據大量試驗數據建立了侵徹深度的計算公式用于工程設計計算[10]。

目前國內外針對巖體介質的侵徹深度計算公式主要有Young公式、Bernard公式、別列贊公式及我國早期擬合公式等7種,文獻[11]根據美國桑迪亞國家實驗室的試驗結果,評價了Young公式預測彈體在低、中強度的巖體中侵徹深度的精度和一致性,認為經驗公式預測的侵徹深度與試驗數據吻合較好。Young公式如下[12]:

(1)

式中:H為彈體侵徹深度;M為彈體質量;A為彈體橫截面面積;v為彈體初始撞擊速度;K為縮尺效應系數。

(2)

N為彈頭性能系數,對于卵形彈:

(3)

式中:Ln為彈體頭部長度;d為彈體直徑;S為巖石的可侵徹性指標,S=2.7(YQ)-0.3,其中Y為巖石無側限抗壓強度(MPa),Q為巖石質量指標,取值范圍在0.1～1.0之間。

代入相關數據得出,SDB小直徑炸彈侵徹花崗巖的深度為1.30 m,數值計算得到的侵徹深度為1.16 m,如圖2,與經驗公式計算數值相近。驗證表明:數值模擬方案選擇合理。

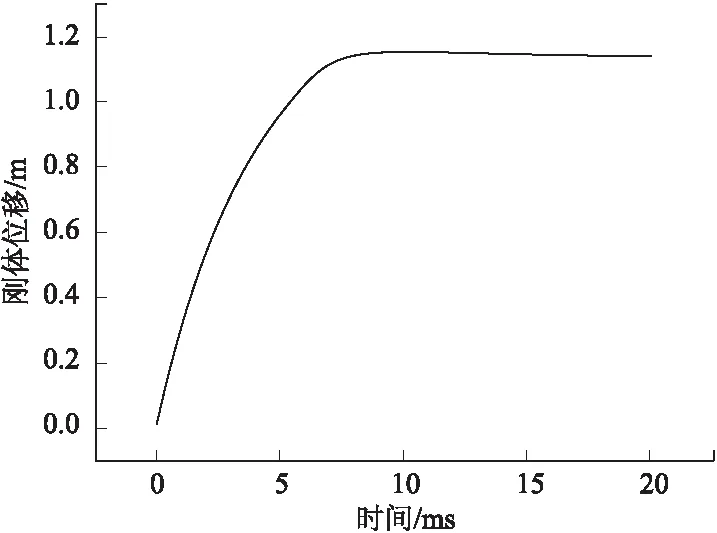
圖2 數值模擬

從圖2可以看出,在9.6 ms時刻之后,彈體停止侵徹,其侵徹深度趨于定值。但之后會出現少量回彈,主要是因為彈體速度為零后,彈坑形成新的自由面,侵徹末端的巖石已無外界能量提供,部分變形逐漸恢復,出現侵徹深度隨時間增長有少量回落的現象。

3 動力效應分析

3.1 受力分析

當壓縮波從一種材料向另一種材料傳播時,會產生反射和透射現象,反射波和透射波的性質主要取決于材料波阻抗ρc的大小。花崗巖的波阻抗為1.40×107kg/(m2·s),大于混凝土的波阻抗0.84×107kg/(m2·s),則應力波由巖石傳遞至混凝土表面時,將發生卸載反射,透射至混凝土的應力波將減小。當混凝土中的透射波傳遞至被覆結構下表面時,空氣的波阻抗顯著小于混凝土的波阻抗,可看作自由面反射,入射壓縮波完全被反射為拉伸波。隨著彈體侵徹的進行,該過程不斷重復發生,被覆結構各部分受壓(拉)力反復作用,在達到最終侵徹深度時刻左右受力最大,圖3較好地說明了這個過程。從圖3還可以看出,拱頂承受的壓(拉)力最大,遠高于其他部位受力,且拱頂最先受力,拱腳最后受力,這是由波的傳播順序決定的。

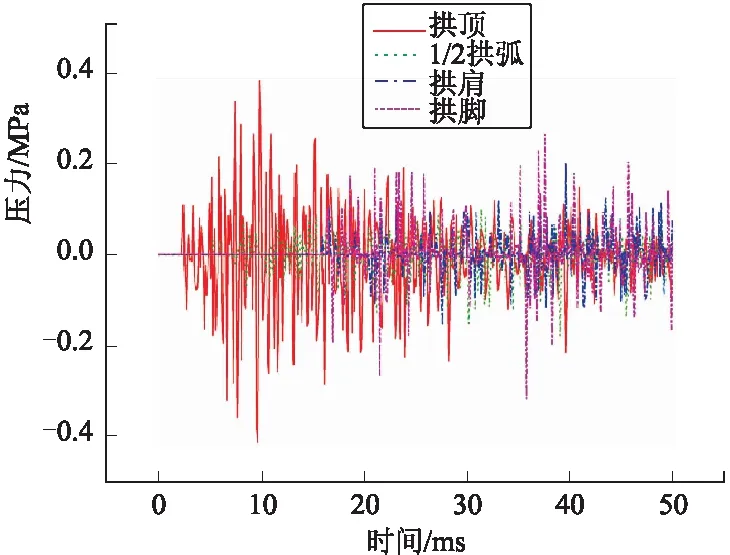
圖3 40 m跨度洞室各部分受力情況

根據彈體侵徹不同跨度、不同埋深的洞室數值模擬結果可知,洞室各部分受力隨時間不斷發生變化,但是所受最大壓(拉)力對被覆結構的破壞起控制作用,各種跨度拱不同部位的受力情況見表3。

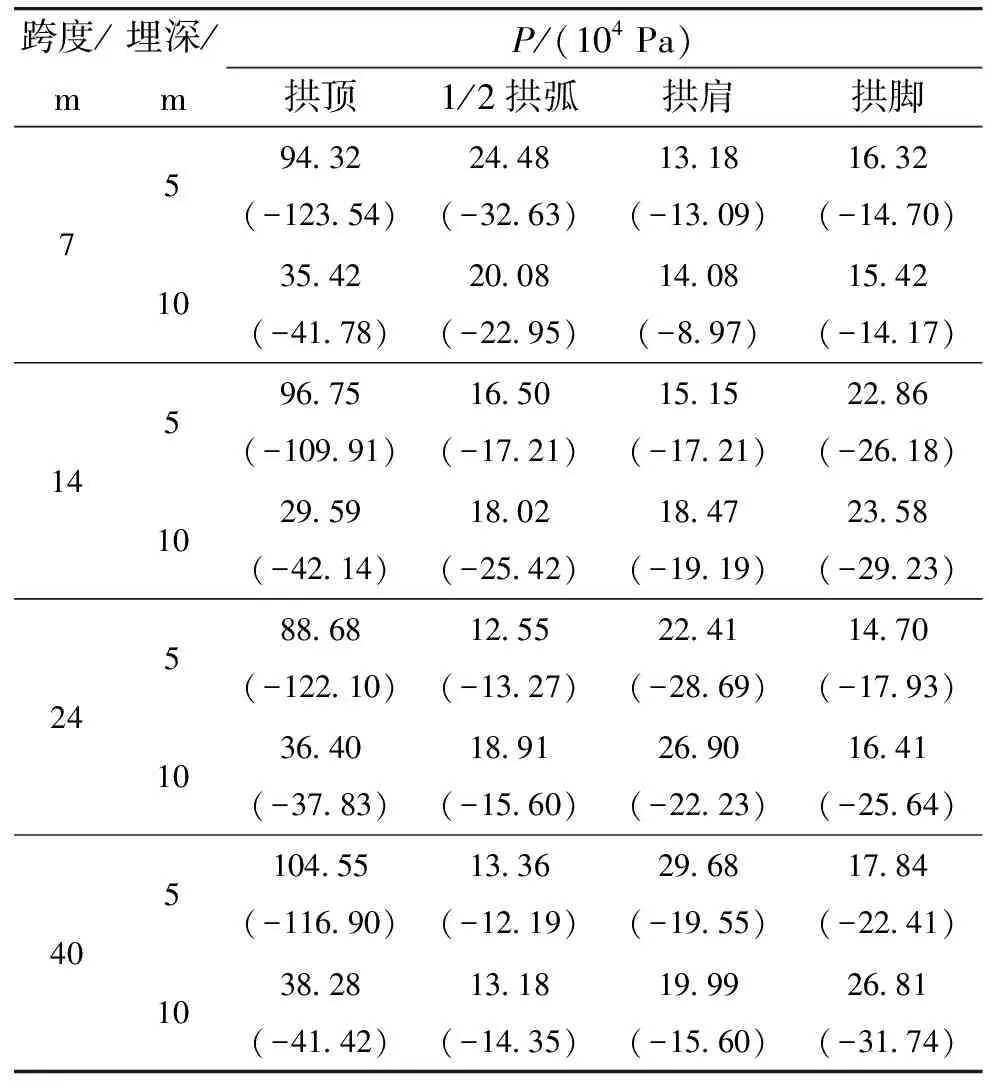
表3 洞室各部分最大壓(拉)力

由表3可知,當埋深相同時,不論跨度多大,拱頂處受力最大,由拱頂向拱腳呈減小趨勢,且跨度不同時拱頂處所受壓力相差較小,表明跨度因素對拱頂受力影響不大;埋深為5 m時,從拱頂處到1/2拱弧處所受壓力下降較快,14 m以下跨度洞室拱肩處壓力會繼續下降,而24 m以上跨度洞室拱肩處所受壓力較大,尤其是40 m跨度洞室,拱肩處壓力達到了296.77 kPa,遠大于1/2拱弧處和拱腳處壓力,這是由于圍巖豎向變形致使拱肩向外變形受到圍巖約束,壓力增大。

當埋深不同時,同一部位的受力情況拱頂下降較快,其他部位變化較小甚至受力增大,拱腳處表現較為明顯。這是因為埋深增加到10 m時,侵徹荷載作用的范圍不再是拱頂局部范圍內,而是作用于整個被覆結構;另一方面,由于跨度較大,應力波傳至其他部位尤其是拱腳部位時間較長,使得應力波的疊加效應各不相同。

3.2 位移響應

當結構受到侵徹荷載作用時,由于應力波的作用,使得結構各部分產生位移響應。圖4和圖5分別為5 m埋深時7 m小跨度洞室和40 m大跨度洞室各部分的豎向位移情況。

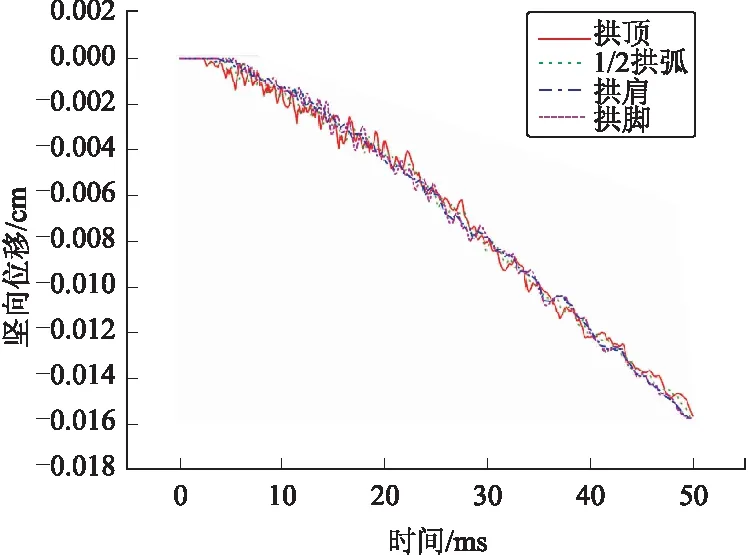
圖4 5 m埋深7 m跨度洞室各部分豎向位移

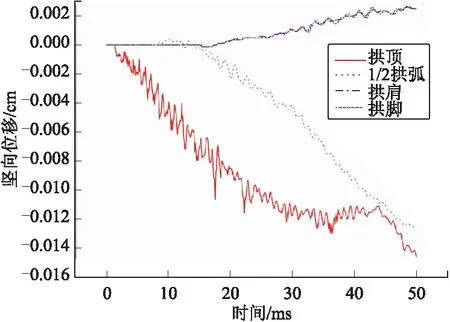
圖5 5 m埋深40 m跨度洞室各部分豎向位移

可以看出,7 m跨度洞室各部分豎向位移基本相同,拱頂位移曲線波動相對劇烈。40 m跨度洞室各部分豎向位移差別較大,拱頂和1/2拱弧位移豎直向下,拱頂受力后立即向下運動,而1/2拱弧在7.5 ms后才開始向下運動,兩處位移下降幅度基本相同,拱頂下降速率先快后慢,1/2拱弧下降速率先慢后快;拱肩和拱腳位移豎直向上,基本同時運動,是因為洞室跨度較大,而直墻高度較小,應力波由拱頂傳播至拱肩所需時間是由拱肩傳播至拱腳所需時間的10倍,且拱肩和拱腳處于同一垂直面上,使得該兩處位移響應相同。

圖6為10 m埋深時40 m大跨度洞室各部分的水平位移情況,可以看出,拱頂水平方向較為穩定,基本不產生運動,隨著與拱頂距離越遠,結構的振幅越大,拱腳的位移響應最為劇烈。在17 ms至27 ms時間內,拱肩和拱腳部位水平位移迅速增大,隨后緩慢增長至45 ms再減小,而1/2拱弧水平位移在0 ms至50 ms時間內增長都比較緩慢。

圖7為10 m埋深時不同跨度洞室拱腳處的水平位移,可以看出,跨度越大,拱腳處開始振動的時間越晚,水平位移越大,位移響應越劇烈。且隨著跨度增大,振動周期逐漸增加,7 m跨度為24 ms,14 m跨度為50 ms,24 m跨度為80 ms,40 m跨度為100 ms。

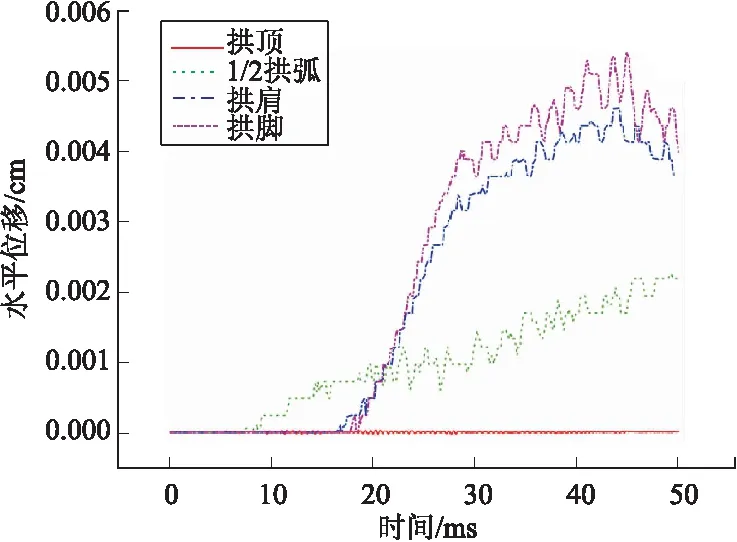
圖6 10 m埋深40 m跨度洞室各部分水平位移

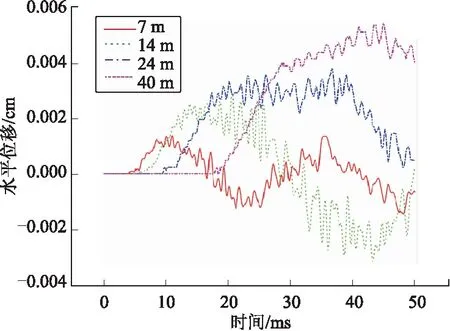
圖7 10 m埋深洞室拱腳處水平位移

4 結論

通過對彈體侵徹作用下不同跨度地下洞室的數值分析,可以得到以下結論:

1)選用Young公式計算侵徹巖石的深度,與數值模擬結果相比較,基本一致,表明數值模擬方案合理,也說明該公式在預估彈體侵徹巖石深度方面使用的普遍性。

2)當地下洞室埋深為5 m時,拱頂處受力最大,14 m以下小跨度洞室拱腳部位受力較大,24 m以上大跨度洞室由于圍巖的約束作用會使得拱肩部位受力較大;當地下洞室埋深為10 m時,被覆結構不再是拱頂范圍局部受力,而是荷載作用于整個被覆結構,且由于應力波的疊加效應,使得拱腳部位受力較大。

3)小跨度洞室各部分豎向位移基本相同,大跨度洞室拱頂和1/2拱弧向下運動,拱肩和拱腳向上運動;不同跨度洞室各部分水平位移拱腳最大,且隨著跨度增大,拱腳水平位移增大。

參考文獻:

[1] 任輝啟, 穆朝民, 劉瑞朝, 等. 精確制導武器侵徹效應與工程防護 [M]. 北京: 科學出版社, 2016: 1-11.

[2] GOLD V M. Analysis of the penetration resistance of concrete: AD-A329 140[R]. [S.l.:s.n.], 2000.

[3] WARREN T L, FOSSUMA F, FREW D J. Penetration into low-strength (23 MPa) concrete: target characterization and simulations [J]. International Journal of Impact Engineering, 2004, 30(5): 447-503.

[4] 鄭振華, 余文力, 王濤. 鉆地彈侵徹高強度混凝土靶的數值模擬 [J]. 彈箭與制導學報, 2008, 28(3): 143-146.

[5] 徐干成, 顧金才, 張向陽, 等. 地下洞庫圍巖外加固抗炸彈侵徹性能研究 [J]. 巖石力學與工程學報, 2012, 31(10): 2064-2070.

[6] 石少卿, 康建功, 汪敏, 等. ANSYS/LS-DYNA在爆炸與沖擊領域內的工程應用 [M]. 北京: 中國建筑工業出版社, 2011: 82-88.

[7] 孫惠香, 許金余, 朱國富, 等. 爆炸作用下跨度對地下結構破壞形態的影響 [J]. 空軍工程大學學報, 2013, 14(2): 90-94.

[8] 沈俊, 劉瑞朝, 楊建超, 等. 彈體侵徹巖體效應試驗與理論研究 [J]. 巖石力學與工程學報, 2008, 27(5): 946-952.

[9] 孫惠香, 許金余, 李慶. 爆炸荷載作用下地下結構破壞模式研究 [J]. 彈箭與制導學報, 2011, 31(5): 89-92.

[10] 吳祥云. 細長彈侵徹防護工程材料靶體的試驗和理論研究 [D]. 長沙: 國防科學技術大學, 2002.

[11] PATTERSON W, BATY R S. 兩個經驗公式與現場試驗結果的比較 [C]∥第十一屆武器效應與結構相互作用國際專題討論會文集. 洛陽：總參工程兵科研三所, 2003: 465-468.

[12] 張德志, 林俊德, 唐潤棣, 等. 高強度巖石侵徹經驗公式 [J]. 兵工學報, 2006, 27(1): 15-18.