一種基于新型符號函數的小波閾值圖像去噪算法

崔金鴿，陳炳權,2，徐慶，鄧波

（1.吉首大學物理與機電工程學院，湖南 吉首 416000；2.吉首大學信息科學與工程學院，湖南 吉首 416000）

一種基于新型符號函數的小波閾值圖像去噪算法

崔金鴿1，陳炳權1,2，徐慶1，鄧波1

（1.吉首大學物理與機電工程學院，湖南 吉首 416000；2.吉首大學信息科學與工程學院，湖南 吉首 416000）

在現有閾值去噪算法的基礎上提出了一種基于新型符號函數的小波閾值圖像去噪算法，該算法提出的新閾值函數具有連續可導、小波系數偏差小、閾值自適應性強等優勢。不僅保留了分解后的低頻小波系數，還有效濾除了高頻系數中的噪聲系數，使得重構后的圖像更接近原始圖像。對高斯白噪聲的Bridge圖像、Lena圖像及含“斑點噪聲”的B超Fetus圖像進行仿真，實驗的結果表明，無論是新閾值函數的視覺效果，還是定量指標PSNR和MSE，均優于現有的閾值圖像去噪算法。其邊緣及細節信息能得到較好的保護，無明顯振蕩，圖像更平滑、均勻，且在復雜噪聲背景下，該方法具有較好的頑健性。

符號函數；小波閾值；去噪；頑健性

[2,3]存在如下缺陷：在硬閾值處理過程中，因為函數不連續，使得信號重構時可能產生振蕩；在軟閾值處理過程中，處理后的小波系數與真實的小波系數存在恒定的偏差，使得處理后的圖像過于平滑，甚至出現邊界模糊等現象。為了彌補缺陷，參考文獻[4-6]對閾值和閾值函數進行了研究，閾值的選取規則要依據適用范圍而定，不同的閾值則有不同的去噪效果；構建閾值函數要具備高階可導性、良好連續性、對邊緣小波系數保護能力強等優勢。

近年來，閾值的選取規則由簡單的固定式逐漸轉向了融合各種算法的自適應控制，諸如GA[7]、改進的PSO算法[8]等；閾值函數由單一的傳統軟硬閾值函數到兩者相結合的半軟閾值函數、折中閾值函數及復雜度高的各種復合改進閾值函數等[9-14]。基于此，本文采用一種基于新型符號函數的復合改進算法，自適應選取閾值，不僅有效解決軟硬閾值出現的振蕩、邊界模糊、平滑過度等問題，去噪效果還要比普通改進方法好，且在處理復雜噪聲環境下的醫學B超圖像時，同樣具有較好的優勢。

2 閾值去噪基本原理

2.1 小波去噪模型

在小波圖像去噪中，高頻信號主要由噪聲信號組成，低頻或者平穩信號主要由有用信號組成。具體的去噪步驟為：首先根據圖像及噪聲的類型選擇合適的小波基及其分解層數，然后利用小波變換對原始圖像進行多尺度分解，再對每層分解后的高頻系數進行閾值量化，保留相對低頻部分，最后重構處理后的系數。

設某一個信號f(n)被噪聲e(n)污染后為s(n)，則噪聲模型為：

其中，e(n)為噪聲，σ為噪聲強度。假設e(n)為高斯白噪聲，令σ=1。小波去噪的目的是抑制e(n)以恢復f(n)，當f(n)的分解系數比較稀松時，去噪效率更高。

2.2 閾值圖像去噪原理

小波閾值圖像去噪是一種基于非參數模型的噪聲抑制方法。圖像經過小波分解后，其小波系數主要分為有用信號系數和噪聲信號系數，圖像有用信息主要表現為低頻信號，邊緣細節信息和噪聲主要表現為高頻信號。

小波圖像閾值去噪的基本思想為：當小波系數小于某一閾值時，該小波系數是噪聲引起的，將其剔除；當小波系數大于某一閾值時，該小波系數是由實際信號引起的，將其保留。

小波圖像閾值去噪的基本步驟如下。

步驟1 選定小波基、分解層數，對含噪聲圖像進行小波分解，得到一組小波系數wj,k。

步驟2 根據小波變換性質可知，圖像小波系數由有用系數和噪聲系數疊加而成，利用合適閾值對小波系數wj,k進行處理，得到小波估計系數wj,k^，要求wj,k^和wj,k的差值盡可能小。

步驟3 對wj,k^進行小波重構，得到去噪后的圖像。

二維含噪圖像閾值去噪流程如圖1所示。

圖1 二維含噪圖像閾值去噪流程

2.3 基于樣本估計的閾值選取

基于式（1）的閾值選取的規則如下。

（1）無偏風險閾值選取規則

該規則針對軟閾值函數，基于Stein無偏似然估計準則自適應地選擇閾值，趨近于理想閾值。對一個給定的閾值，將其非似然估計最小化，就得到所選的閾值。

（2）通用閾值選擇規則

（3）啟發式閾值選擇規則

該規則的閾值是一種最優預測變量，是上述2種規則的融合。

（4）最小最大閾值選擇規則

該規則產生一個最小均方誤差極值，并由它設計估計器，以實現最大均方誤差的最小化。

每一種閾值選擇規則都有相應的適用范圍，前兩種方法相對保守，但可以有效地保留有用信息高頻系數；后兩者雖然可以有效濾除高頻系數，但可能將高頻系數中的有用信息當作噪聲濾除掉，在選擇閾值時要視具體情況而定。

3 小波閾值圖像去噪算法

3.1 軟硬閾值去噪算法

Donoho和Johnstoni[2,3]提出的軟硬閾值去噪算法，首先確定小波系數的通用閾值，采用硬閾值或軟閾值對小波系數做閾值處理。硬閾值法保留大于閾值的小波系數，并將小于或等于閾值的小波系數置零；軟閾值法是把大于閾值的小波系數向零收縮，將小于或等于閾值的小波系數置零，相關模型如下。

硬閾值法模型：

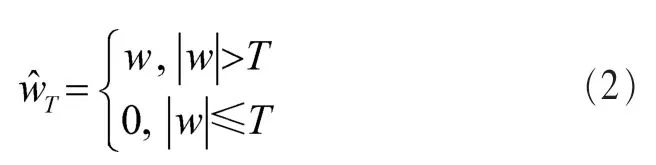
軟閾值法模型：

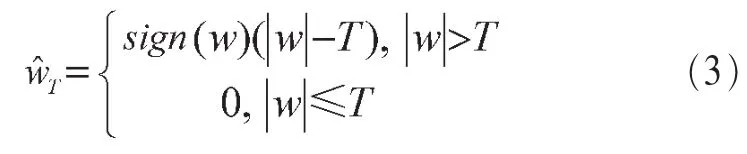
其中， ^wT為閾值處理后的小波系數，w為原始小波系數，T為閾值。在圖像去噪處理中，由于硬閾值在閾值點處不連續，使得處理后的圖像產生振蕩，而軟閾值由于小波原始系數和閾值處理后的小波系數存在一定的偏差，勢必出現邊緣模糊等失真現象。

3.2 改進的閾值圖像去噪方法

由于軟硬閾值函數在去噪過程中，存在邊緣模糊、平滑過度等失真現象，因此，設計一種新閾值函數，既能實現閾值函數的功能，又能使去噪后的圖像具有清晰的邊界和較低的失真性，是小波去噪的關鍵技術之一。合適的閾值函數應具備以下2個基本條件[15]：連續性較好，防止數據重構時出現振蕩；對邊緣小波系數保護能力強，防止數據重構出現模糊，且滿足關系式[16]：其中，E為偏差之和，n為絕對值大于閾值的小波系數。參考文獻[4,9,11]閾值圖像去噪模型如下。

（1）半軟閾值法去噪模型[4]

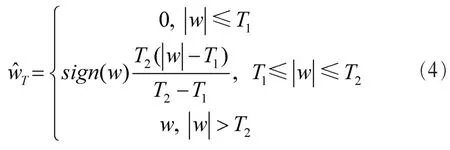
（2）軟硬閾值折中法去噪模型[9]

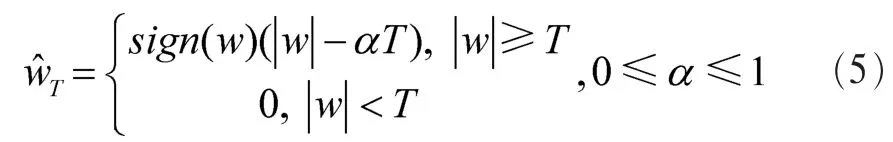
（3）改進閾值法去噪模型[11]

在式（4）～式（6）中，α和m為調節系數，根據去噪效果來決定大小，T1和T2分別為上下限閾值。其中式（5）在上下限閾值點連續，在式（4）中，當α=1時，在式（3）中，當m=0時，閾值函數在閾值T點都保持連續，避免了硬閾值函數的不連續，且在區間|w|≥T都存在高階可導；同時，隨著|w|的增大，|w-^wT|逐漸減小，當|w|→∞時，|w-^wT|→0，這樣就有效解決了軟閾值函數出現恒定偏差的問題。上述3種模型都在傳統軟硬閾值去噪效果上有了不同程度的改善，但是在實際應用中仍然存在一定的不足，圖像邊緣信息屬于高頻部分，對應的小波系數往往也偏低，直接置零，勢必造成圖像部分信息缺失。

4 基于新型符號函數的去噪算法

本文在式（4）～式（6）的基礎上提出了一種新閾值函數，該函數具備了連續可導、小波系數偏差小等優點，模型中含有指數函數，增強了閾值函數的收斂性。在傳統閾值或改進算法中，一般只對分解后的小波系數絕對值大于或者等于閾值的部分做了處理，而對于分解后小波系數絕對值小于閾值的部分未作閾值量化處理，該部分系數里可能含有少量的有用系數，全部置零會在一定程度上影響去噪的效果。本文提出的基于新型符號函數的去噪算法，不僅對絕對值大于或者等于閾值的小波系數進行了閾值量化處理，還對絕對值小于閾值的小波系數進行高階函數量化處理。

針對絕對值小于閾值的小波系數，為保證在提取有用信號信息的同時避免噪聲再次進入，引入下限閾值（根據小于閾值T這部分小波系數中噪聲與有用信號所占的比例關系而定），經過試驗得到比例系數為0.4時，效果最佳。然后將小波系數絕對值位于兩閾值之間部分進行高階函數處理，低于下限閾值的小波系數是由噪聲引起的，將該部分小波系數置零。這樣就可以有效提取小波系數中的有用信號信息，剔除噪聲信號。

具體的實現步驟如下。

步驟1 對于小波系數絕對值大于閾值部分由符號函數向閾值點作收縮處理，保留圖像大部分有用信息。

步驟2 引入下限閾值，將小波系數位于兩閾值之間部分進行高階函數處理，提取剩余少量的有用信息。

步驟3 將小于下限閾值的小波系數置零。

新型符號函數模型如下。

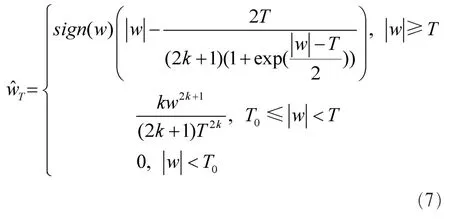
其中，sign（·）為符號函數，T為該函數的上限閾值。T0為下限閾值，且T0=εT，ε、k為調節參數，可以根據去噪的效果合理地調節ε、k的取值。在本文實驗中，當ε取0.4時，基本滿足這部分系數中噪聲與有用信號的比例關系。

當k=0時，式（7）可變為：

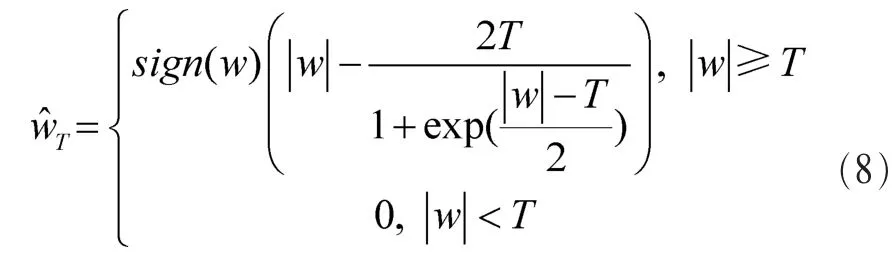
當k=1時，式（7）又可變為：

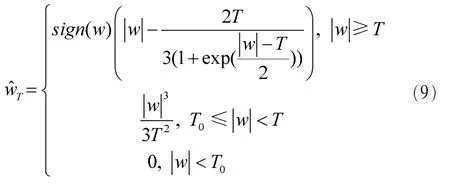
顯然，當|w|=T，k=0時，上分段函數會向零收縮，下分段函數結果取零（^wT=0）；當^wT→0時，函數在閾值T點連續，但在下限|w|＜T函數卻變成了0，只在|w|≥T區間上存

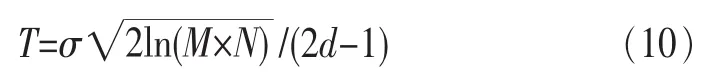
其中，M、N是圖像的大小，σ=median(|w|)/0.674 5為噪聲標準差，d為圖像的分解尺度。

由式（10）可知，當圖像尺寸一定，圖像的分解尺度增大時，整體閾值隨之減小，這樣在去噪時就能保留有效信息，有效防止過“扼殺”。當d=1時，式（10）即通用閾值T。

當每層系數分解完后，首先，通過新閾值函數對每一層小波系數中的高頻系數閾值進行量化處理，然后，將處理后的系數進行重組，就能得到去噪后的圖像。隨著分解層數和小波基的不同，圖像去噪后的效果也會有差異，為保證較好的去噪效果，分解層數設為3層，小波基設為db8。實驗中Bridge圖像和B超Fetus圖像的3層分解結果如圖2所示。在高階可導的函數。當|w|=T，k=1，在|w|＜T或|w|≥T的區間上，則有^wT→T/3，即在閾值T點連續，避免了硬閾值重構信號時振蕩的產生；當|w|→∞，^wT→w時，即w增大至近似等于^wT時，避免出現軟閾值中w與^wT之間存在一定偏差的缺陷。另外，在|w|＜T時，一般的改進閾值函數通常置零，從而忽略了該部分系數中含有的少量有用小波系數，而新閾值函數通過引入下限閾值，定義了區間T0＜|w|＜T上的函數表達式，通過調節參數k的大小來篩選出有用系數，靈活性強，可根據不同的需要得到實用性強的閾值函數，且函數表達式無過多的參量，計算復雜度小。

通用閾值常常把所有尺度上的小波系數默認為一致，忽略了有用信號和噪聲信號的差異。本文新閾值函數的閾值T在參考文獻[11,17]的基礎上考慮到圖像大小對閾值的影響，引入分解尺度d，構造了如下自適應閾值模型：

圖2 含噪圖像的3層分解（小波基db8）

從圖2可知，每層能量分布都不相同，即每層中分解后的高頻系數與低頻系數都不一樣。同時，在圖2(a)中發現了少許噪聲點，在圖2(b)中噪聲類型較為復雜，分解后系數分布不均勻，所以在分解系數后實物輪廓有些模糊。

5 實驗仿真結果

本文仿真在MATLAB 2012a軟件平臺進行，在Intel Core i3-3240 CPU的PC上分別用傳統軟硬閾值法、折中閾值法、半軟閾值法、參考文獻[11]方法以及本文新閾值法對3幅圖像（Bridge圖像、Lena圖像及B超Fetus圖像）進行了二維圖像仿真實驗，并將這幾種閾值函數去噪結果和新閾值法進行對比，仿真結果如圖3～圖5所示。為保證具有較好實驗效果，實驗中k取1。

圖3 針對Bridge圖像的各種方法去噪結果對比

圖4 針對Lena圖像的各種方法去噪結果對比

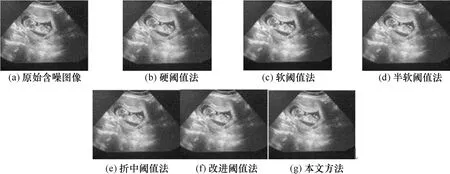
圖5 針對B超Fetus圖像的各種方法去噪結果對比（k=1）

仿真實驗中，Bridge圖像采集于某大學校園雨后的風雨橋，含噪聲方差為20的高斯白噪聲，大小為115 dpi× 85 dpi；Lena圖像為經典實驗圖像，由圖庫下載，大小為256 dpi×256 dpi；B超Fetus圖像來自某醫院B超機視頻輸出接口，中心頻率為35 Hz，大小為105 dpi×100 dpi。在實際圖像采集中，外界采景易受天氣、光線等因素的影響，勢必造成采集到的圖像模糊，其含有較多高斯白噪聲，所以選擇景物Bridge圖像和人物Lena圖像較為合理。選擇B超Fetus圖像是因為現代B超圖像在形成過程中會因為X射線、機械噪聲、信道噪聲等交織形成混合噪聲“斑點噪聲”，嚴重干擾對病情的診斷等。針對B超圖像出現的噪聲問題，本文基于參考文獻[18,19]的研究，重點驗證了本文提出的新閾值函數對B超圖像去噪的有效性及優越性。

從圖3可知，圖3（d）要比圖3（c）平滑很多，湖中的倒影稍顯模糊，邊緣信息有丟失。圖3（f）、圖3（g）、圖3（h）有明顯的改善，能夠更清晰地看到橋上面的行人，圖像清晰度都有不同程度的提高。但是圖3（f）、圖3（g）的清晰度在提高的同時，噪聲也被放大，綜合對比，新閾值法處理下的圖3（h）去噪效果較好，幾乎看不到噪聲的影響。同樣在圖4中，圖4（d）、圖4（e）出現明顯的模糊現象，無法識別Lena面部表情，圖4（g）、圖4（h）相對來說，去噪效果較為明顯，但圖4（g）景深突變處有輕微的失真現象。

由圖5知，針對具有復雜噪聲的 B超Fetus圖像，傳統的軟閾值處理效果并不理想，而在改進閾值方法中，圖5（e）、圖5（f）、圖5（g）清晰度都有不同程度的提高，其中圖5（g）去噪效果提高得較明顯，Fetus圖像邊緣更清晰，且沒有過度的平滑現象，胎兒位置可以被細致地觀察到。

本文利用均方誤差（mean squared error，MSE）、峰值信噪比（peak signal to noise ratio，PSNR），分別對圖3～圖5進行客觀評價估計，結果見表1。

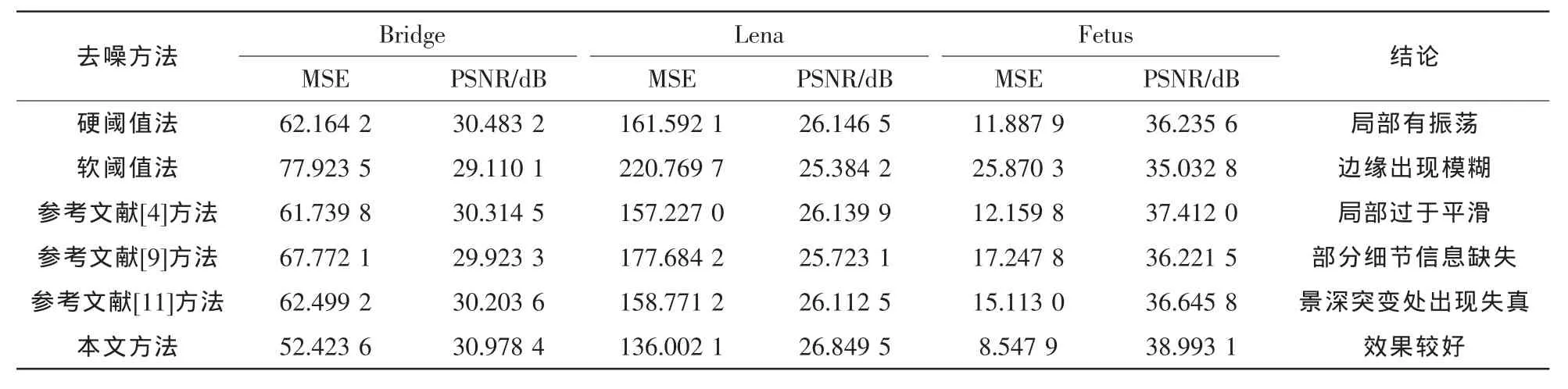
表1 各種圖像去噪算法客觀評價結果

從表1可知，軟硬閾值法及半軟閾值法去噪效果相對較弱，特別是處理B超Fetus圖像效果不是太好，相比之下，新閾值函數更有效地降低了均方誤差，提高了峰值信噪比，尤其在處理B超Fetus圖像時，相比其他方法，MSE最大降低17．182 6，PSNR最大超出4．758 9 dB。

在實際去噪的過程中，無論小波系數絕對值大于還是小于閾值，都能通過調節值大小得到比較好的閾值量化效果。為進一步討論k值對去噪效果的影響，實驗選取k∈[0,3]，由MATLAB仿真實驗，數據結果見表2及圖6。

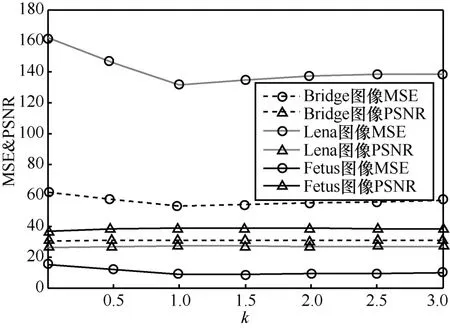
圖6 3幅圖像在不同k值時的去噪結果（k∈[0．3]）

表2 不同k值的去噪結果(k∈[0,3])

由表2及圖6可知，當時，去噪處理后Bridge圖像、Lena圖像及Fetus圖像的峰值信噪比（PSNR）相對較高，而均方誤差（MSE）相對較低，達到了最佳效果。

為了探究本文方法對嚴重噪聲污染圖像的去噪能力，實驗中對Bridge圖像和Lena圖像分別添加噪聲方差為10、20、30、40、50的高斯白噪聲。采用不同方法對添加不同噪聲方差的去噪效果如圖7所示。

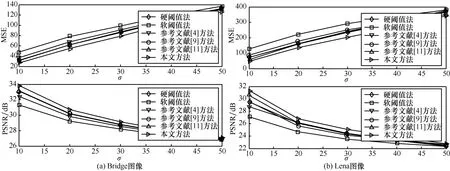
圖7 各種方法處理后的Bridge圖像和Lena圖像的MSE與PSNR對比結果

當噪聲污染的程度增大時，各種方法的去噪能力都有所減弱，但本文提出的新閾值函數處理后的MSE始終小于其他方法，PSNR始終大于其他方法，去噪效果更好。

6 結束語

為了彌補傳統閾值去噪方法的不足，獲取更具有清晰邊界、平滑均勻的圖像。本文提出了一種基于新型符號函數的小波閾值圖像去噪方法，改進后的閾值函數具備良好的實用性，無論小波系數的絕對值大于或小于閾值，都能找到適應的閾值函數，且能夠根據圖像尺寸大小自適應選取閾值。實驗證明，該法具有較好的頑健性，不僅在高斯噪聲圖像中具有較強的去噪能力，而且在有復雜噪聲的B超圖像下，同樣也具備很好的去噪效果。

在B超圖像去噪中，因為“斑點噪聲”所含噪聲類型復雜，無法判定本文方法對“斑點噪聲”的污染程度去噪效果，所以只對含高斯白噪聲Bridge圖像做了深入探究。下一步工作主要研究該法對含不同噪聲污染程度的B超圖像去噪能力，并找出一個來衡量“斑點噪聲”污染程度的參考標準，使該法在研究動態圖像、視頻圖像等復雜圖像中得到更好的應用。

參考文獻：

[1]謝杰成,張大力,徐文立.小波圖像去噪綜述[J].中國圖象圖形學報,2002,7(3):209-217. XIE J C,ZHANG D L,XU W L.Overview on wavelet image denoising[J].Journal of Image and Graphics,2002,7(3):209-217.

[2]DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

[3]DONOHO D L,JOHNSTONE I M,KERKYACHARIAN G,et al.Wavelet shrinkage:asymptopia[J].Journal of Royal Statistics Society Series(B),1995(57):301-369.

[4]BRUCE A G,GAO H Y.Understanding WaveShrink:variance and biasestimation[J].Biometrika,1996,83(4):727-745.

[5]GUNAWAN D.Denoising images using wavelet transform[C]// 1999 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing,Aug 22-24,1999,Victoria, BC,Canada.New Jersey:IEEE Press,1999:83-85.

[6]SHARK L K,YU C.Denoising by optimal fuzzy thresholding in wavelet domain[J].Electronics Letters,2000,36(6):581-582.

[7]MUKHOPADHYAY S,MANDALJ K.Wavelet based denoising of medical images using sub-band adaptive thresholding through genetic algorithm[J].Procedia Technology,2013,10(2):680-689.

[8]GUPTA D K,PAWARV S,JAIN Y K.Wavelet based multilevel sub-band adaptive thresholding forimage denoising using modified PSO algorithm [J].International Advanced Research Journal in Science,2015,12(2):24-30.

[9]張遵偉,羅曉輝,張德勝,等.閾值改進算法在小波去噪中的應用[J].西華大學學報(自然科學版),2010,29(5):43-45. ZHANG Z W,LUO X H,ZHANG D S,et al.An improved thresholding denosing algorithm and its application in wavelet denoising [J].JournalofXihua University(NaturalScience Edition),2010,29(5):43-45.

[10]楊鑫蕊.改進的小波閾值去噪算法研究 [D].哈爾濱:哈爾濱理工大學,2014. YANG X R.Research on improved wavelet threshold denoising algorithm [D].Harbin:Harbin University ofScience and Technology,2014.

[11]王琪,程彬,杜娟,等.一種改進的小波閾值圖像去噪方法[J].計算機與現代化,2015(4):65-69. WANG Q,CHENG B,DU J,et al.An improved method for denoising of wavelet threshold images[J].Modern Electronics Technique,2015(4):65-69.

[12]謝家林,李根強,謝家麗,等.改進閾值函數在圖像去噪中的應用[J].空軍工程大學學報(自然科學版),2016,17(1):72-76. XIE J L,LI G Q,XIE J L,et al.Research on the application of the improved threshold function to image denoising[J]. Journal of Air Force Engineering University(Natural Science Edition),2016,17(1):72-76.

[13]JITHA C R.Image denoising by modified overcomplete wavelet representation utilizing adaptive thresholding algorithm[J]. International Journal of Scientific& Engineering Research, 2015,4(6):802-813.

[14]BHANDARI A K,KUMAR A,SINGH G K,et al.Performance study of evolutionary algorithm for different wavelet filters for satellite image denoising using sub-band adaptive threshold[J]. Journal of Experimental&Theoretical Artificial Intelligence, 2015,28(1-2):71-95.

[15]杜春.運動模糊圖像恢復和小波閾值去噪算法研究 [D].長沙:國防科學技術大學,2008. DU C.Motion blurred image restoration and wavelet threshold denoising algorithm analysis[D].Changsha:National University of Defense Technology,2008.

[16]袁開明,舒乃秋,孫云蓮,等.基于閾值尋優法的小波去噪分析[J].武漢大學學報(工學版),2015,48(1):74-80. YUAN K M,SHU N Q,SUN Y L,et al.Wavelet denoising based on threshold optimization method[J].Engineering Journal of Wuhan University,2015,48(1):74-80.

[17]VERMA S,KHARE N.Denoising of computed tomography images using wavelet transform [J].International Journal for Innovative Research in Science&Technology,2015,1(8): 21-29.

[18]侯宏花,陳樹越,郭保全.醫學B超圖像降噪處理的三種方法比較[J].測試技術學報,2003,17(3):262-264. HOU H H,CHEN S Y,GUO B Q,et al.Comparison of three methods in decreasing noise of medical B model ultrasonic images[J].Journal of Test and Measurement Technology,2003, 17(3):262-264.

[19]張聚,王陳,程蕓.小波與雙邊濾波的醫學超聲圖像去噪[J].中國圖象圖形學報,2014,19(1):126-132. ZHANG J,WANG C,CHENG Y.Despeckling for medical ultrasound images based on wavelet and bilateral filter[J]. Journal of Image and Graphics,2014,19(1):126-132.

A wavelet threshold image denoising algorithm based on a new kind of sign function

CUI Jinge1,CHEN Bingquan1,2,XU Qing1,DENG Bo1
1.College of Physics and Electromechanical Engineering,Jishou University,Jishou 416000,China 2.College of Information Science and Engineering,Jishou University,Jishou 416000,China

Based on the existing threshold denoising algorithm,a threshold denoising algorithm based on the new symbolic function was proposed.The new threshold function has advantages of continuous guidance,small deviation of wavelet coefficient,strong threshold adaptability and so on.It not only preserved the low-frequency wavelet coefficients,but also filtered the noise coefficients in the high-frequency coefficients effectively,so that the reconstructed image was closer to the original image.The simulation results of Bridge image,Lena image and B-mode Fetus image with Gaussian white noise show that the visual effect of both the new threshold function and the quantitative indicators PSNR and MSE are better than the existing threshold image denoising algorithm.The edge and detail information can be better protected,have no obvious oscillation,the image is smoother and even, and the method has good stubbornness under the background of complex noise.

sign function,wavelet threshold,denoising,robustness

TP391.4

A

10.11959/j.issn.1000-0801.2017012

1 引言

崔金鴿（1991-），男，吉首大學物理與機電工程學院碩士生，主要研究方向為信號處理技術。

陳炳權（1972-），男，博士，吉首大學物理與機電工程學院副教授，主要研究方向為圖像處理與智能控制。

徐慶（1988-），男，吉首大學物理與機電工程學院碩士生，主要研究方向為圖像處理技術。

鄧波（1990-），男，吉首大學物理與機電工程學院碩士生，主要研究方向為圖像編碼壓縮感知。

2016-10-11；

2017-01-04

陳炳權，cba2005@yeah.net

湖南省自然科學基金資助項目（No.2016JJ4074）；湖南省教育廳科學研究項目（No.14C0920）；吉首大學課題資助項目(No.Jdy16023,No.15JDY032)

Foundation Items:Hunan Provincial Natural Science Foundation of China(No.2016JJ4074),Project of Hunan Provincial Education Department of China(No.14C0920),Project of Jishou University Subject(No.Jdy16023,No.15JDY032)

在圖像的采集中，由于受到光線強度、噪聲等外界因素的干擾，導致圖像質量下降。圖像去噪的目的是盡可能保留原始圖像的信息，凸顯邊緣和細節信息。傳統圖像去噪算法，通常由傅里葉變換對含噪信號進行處理，由濾波器過濾掉含噪信號中的高頻成分，再由傅里葉逆變換還原出有用的信號，處理后的圖像會出現邊緣局部細節缺失等現象。小波變換具有經典傅里葉變換所不具有的時間—頻率的局部性，能夠呈現出圖像任意局部細節，更好地保護邊緣和細節信息。近年來，小波變換以其去相關性、多分辨率性、低熵性、選基靈活性等特性，廣泛應用于圖像去噪領域。目前，小波圖像去噪的方法大體可以分為小波萎縮法、投影法、相關法3類[1]。Donoho等[2,3]提出的閾值萎縮方法（WaveShrink），包括硬閾值（hard threshold）法和軟閾值（soft threshold）法，給出了通用閾值真正意義上使小波系數閾值量化去噪成為可能，并且取得了較好的視覺效果，證明了WaveShrink的最優性。