新人教版數學四年級上冊“角的度量”教學難點破解
韓江土
[摘 要]“角的度量”是培養學生動手能力和空間觀念的重點內容。然而“角的度量”的教學卻是一個公認的老大難問題,學生學習困難重重。要破解這一難題,教師應分析學生度量角時產生的錯誤原因,并提出針對性的破解方法。
[關鍵詞]角的度量;教學難點;破解
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2017)11-0022-02
“角的度量”是小學階段學生需要學習的重要操作技能之一,但“角的度量”涉及的數學概念多,知識盲點多,操作程序復雜。這部分內容的教學是一個公認的老大難問題,也是許多教師感到頭痛的一個知識點,對于動作不夠協調的四年級學生來說,更是一次關于手和腦的挑戰。雖然新版教材相對于舊版教材在邏輯脈絡上更加清晰(舊教材的邏輯主線:量角的大小——用量角器——認識量角器——認識度量單位1°——學習度量方法——練習鞏固;新教材的邏輯主線:量角的大小——用一定大小的角作為度量單位進行度量——讓度量結果合理些需要合適的度量單位——認識度量單位1°——認識量角器——學習度量方法——練習鞏固),但我用新版教材教學完后發現,對大部分學生而言,量角的過程仍是那么艱難:頂點和中心點重合簡單,而要把零刻度線和角的一邊重合,使另一邊在刻度內并準確讀數卻非易事(度量不同方位的角時更是如此),要分清內外刻度更是困難重重(尤其是反向旋轉和不同方位的角)。
基于此,我對學生度量角時存在的問題進行了梳理,并提出了針對性的破解方法。
一、量角器的擺放問題
[錯誤現象]學生在度量角的過程中,出現了如下圖所示的量角器擺放現象,且數量超過50%。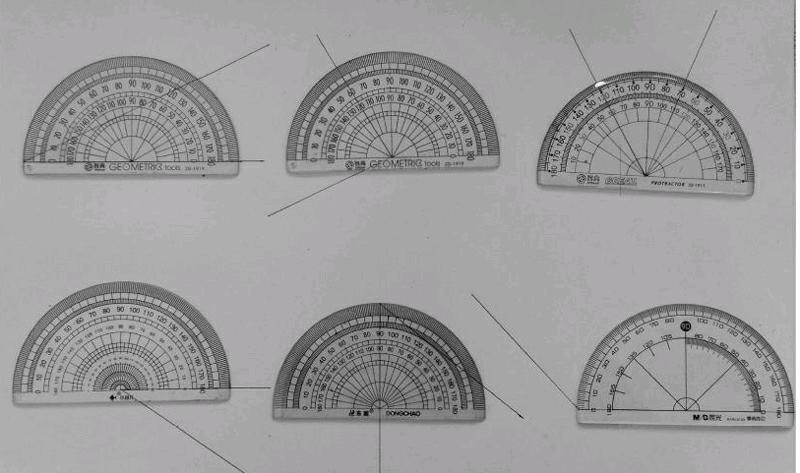
[原因與破解方法]
通過和學生交流,筆者發現造成學生錯誤擺放量角器的原因不少,具體如下:
原因一:學生對角的概念理解不深。學生看到的角只是兩條射線,而不是一個平面圖形。他們沒有從空間上去認識角,更不知道所量的角的動態范圍是哪些。
破解方法:從動態層面來描述角,即“角可以看作由一條射線繞著它的端點,從一個位置旋轉到另一個位置所形成的圖形”,使角動起來,體現“角”的各要素(邊、度量單位)在角的構成過程中的主要作用,強化學生對角的概念的系統性認識,真正揭示角的本質內涵。在教學中,我讓學生把兩條手臂伸開,當作角的兩條邊,把身體當作角的頂點,然后讓學生跟著我,先是兩臂重合,然后一臂不動,另一臂慢慢展開,體驗角由小變大的過程。這樣,學生便會明白所有角都是這樣由小變大的。
原因二:學生看不到量角器上的角。為了測量方便,量角器都做成半圓形,把半圓平均分成180等份,每一等份所占的角的度數就是1°,這個1°同時也是角的度量單位。在量角器上,我們能找到0°~180°之間所有的角,可是學生在量角器上只看到刻度,卻看不到量角器上的刻度所對應的角。
破解方法:讓學生認識量角器,重點放在“在量角器上找大小不同的角”上。這里可分認識量角器、認識1°角和在量角器上找大小不同的角三個層次進行教學。認識量角器時,先讓學生仔細觀察自己的量角器,看看有什么發現。學生基本能觀察到“中心點”“0°~180°的刻度線和刻度”等基本特征。認識1°角時,教師先出示一個1°角的模型實物,讓學生猜猜這個角有多大,然后把這個角放在量角器上(注意量角器要大一些)并投影出來,讓學生看到角的大小剛好占量角器一小格的刻度,告訴學生這個角的度數就是1°。移動這個角,放到量角器的不同位置,形象地展示了,即使在不同的位置,1°的角都只占一小格,以此深化學生對1°角的理解。在此基礎上,讓學生在量角器上找大小不同的角:先找標有度數的刻度上的角,如30°、60°、120°的角,讓學生指出角的頂點和兩條邊(有的學生找出的角不是從0°刻度線開始的,而是在量角器的中間,如30°的角的兩邊分別在刻度20與50上,教師應充分給予肯定);再找沒有標明度數的刻度上的角,如38°、52°的角,引導學生認真看清楚量角器上的刻度,同樣指出角的頂點和兩條邊的位置。這樣,學生就能在量角器上看到角了。
原因三:即使看到了量角器上的角,也不知道怎樣才能使量角器上的角與所測量的角重合,從而導致測不出角的度數或是讀數錯誤。
破解方法:利用“三重合”(課本上是“二重合”)讓學生用量角器上的角去“重合”所測量的角。即用量角器上的角的頂點(即中心點)去“重合”要量的角的頂點,用量角器上的零刻度線去“重合”角的一條邊,用量角器上的角的終邊去“重合”角的另一條邊,這樣量角器上的角的終邊所在的刻度就是所測角的度數。
二、量角器的讀數問題
[錯誤現象]在解決了量角器的擺放問題后,讀數時,很多學生都讀錯了,如把50°的角讀成130°,把125°的角讀成55°等,整個讀數過程雜亂無章。
[錯誤原因]學生讀數雜亂無章的原因無非是混淆的量角器的兩圈的刻度。
[破解方法]通過對錯誤原因的分析,我總結了以下四種破解方法。
方法一:先區分銳角和鈍角,再讀度數。讓學生在學會擺放量角器的基礎上再讀度數,只要先判斷出所量的角是銳角還是鈍角,就不會弄混量角器上的兩圈刻度。
方法二:用“口訣”幫助讀數。鑒于學生讀數的困難較大,教師可用朗朗上口的口訣來幫助學生讀數。如“中心對頂點,0線對一邊,再看另一邊,0度在內看內圈,0度在外看外圈”,強調從0度開始往上數,就能找到角的度數。
方法三:把角看成一個動態的過程再讀數。學生之所以分不清內外圈,找不對數的方向,原因是把角看作是靜止的圖形,學生孤立地看待角的兩邊,以為像量線段、看鐘表一樣,只要把一邊對準0度,另一條邊指著幾就讀幾。如果學生能把靜態的角理解成是從0度開始,慢慢打開,而度數也隨之增加的一個動態圖形,那么讀數問題就迎刃而解了。
方法四:用改進的量角器來量角讀數。現在用的量角器及學生買來的量角器,上面都有兩組0°~180°的刻度,并且兩組刻度的方向是相反的。正是這兩組方向相反的刻度,才導致學生讀數出錯。經多方走訪,我找不到只有一組刻度的量角器,對此我自己動手改進。根據有關資料和學生的認知規律可知,逆時針方向旋轉形成的角,是一個正角,學生容易理解它的大小,度量角時“零刻度線”在右為好,因此可保留從右邊0度開始的一組刻度,把另一組刻度用修正液覆蓋。用這樣的量角器,學生量角時輕松多了,只要強調從0度開始讀,學生都能正確地度量出角的度數。
(責編 黃春香)

