將數學思想滲透在課堂教學中

康登輝

[摘 要]數學的課堂教學離不開數學思想的滲透，數學思想的滲透需要以數學知識為載體。教師應注重讓學生在具體數學知識的獲得和感悟數學思想。

[關鍵詞]數學思想；數形結合；轉化；建模

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）11-0087-01

數學課程標準指出：“通過義務教育階段的數學學習，學生能獲得適應社會生活和進一步發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗。”但是在學生的數學學習過程中，教師往往過分關注學生對知識的掌握情況及掌握的熟練程度，忽略學生獲得知識的過程以及在這個過程中的數學思想的滲透。日本數學教育家米山國藏指出：“作為知識的數學出校門不到兩年就忘了，唯有深深銘記在頭腦中的數學精神、數學思想、研究的方法和著眼點等，這些隨時隨地發生作用，使人終身受益。”因此，教師在注重知識獲得的同時，還應注重思想方法的滲透，讓學生習得終身受益的思想方法。

一、巧用數形結合，促進知識框架的建構

數學家華羅庚先生說：“數缺形時少直觀，形少數時難入微。”例如，教學“表內乘法”時，乘法的概念是學生學習的重點和難點。在教學中，教師首先出示一幅動物場景圖，引導學生觀察并說一說從圖中發現了什么。學生在觀察和交流中形成了豐富的感性認識，當教師拋出“兔子有多少只？雞有多少只？”的問題時，學生很肯定地說應把“幾個幾相加”，在學生建立豐富的“形”的表象后，教師順勢指出幾個數相加可用乘法計算。

借助“形”的呈現，促進學生對乘法意義的理解。數與形的有效結合，促進了學生對乘法含義的內在建構，在意義的建構過程中，學生初步感受到了朦朧的數形結合思想，促進了學生數學思想的積累，有效提升了學生解決問題的能力。

二、妙用轉化思想，促進數學思想的形成

數學知識具有一定的邏輯關系，可借助舊知展開對新知的學習。例如，教學“分數乘整數”時，學生對同分母分數加法及整數乘法已經有了清晰的認識，課始，教師引導學生復習相關知識后，出示例題：“做一朵花需綢帶3/10米，做3朵花需綢帶多少米？”學生聯系舊知，自然會想到：3個3/10是多少？在獨立探索計算方法的環節中，學生借助同分母分數相加的計算方法及分數乘整數的意義，很順利地得出了3×3/10。在師生互動交流環節中，學生圍繞3×3/10計算方法的探索過程展開交流，最終得出“3個3/10相加，分母不變，分子相加，分子是3個3相加，可以用3×3”表示的結論，即分母不變，分子與整數相乘。

通過交流，學生借助舊知推出新知，推理過程中突出了轉化思想，促進了學習方法的掌握，有效促進數學學習能力的提升。

三、運用建模思想，促進知識模型的建構

低年級學生的思維處于形象階段，對數學知識的理解往往需要借助“拐杖”，即將抽象的知識形象化，才能完成知識的建構。

例如，教學“9加幾”時，教師一開始有序地呈現了“10+1，10+2，10+3，10+4，10+5，10+6，10+7，10+8，10+9”等題目，組織學生討論：“通過剛才的計算，你發現了什么？”通過交流，學生發現： 10加幾就是十幾。接著教師出示題目：一盤9個桃，一盤4個蘋果，一共有多少個水果？學生思考后列出算式“9+4”，然后教師引導學生思考：“算式的結果是多少？你是怎樣計算的？”

生1：我看著圖形一個一個地數，共有13個。

生2：我先把9記在心里，然后往后再數4個數，一共是13個。

生3：我根據桃子和蘋果的數量，在本子上畫出相應數量的圓圈，再數圓圈的數量，共有13個。

生4：因為10加幾等于十幾，4可以分成1和3，先從4里拿出1與9合成10，再算 10+3=13，所以共有13個。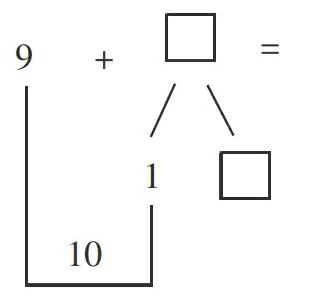

教師根據學生的回答，組織學生進行討論：“你喜歡哪一種解題方法？為什么？”學生各抒己見，最后得出結論：先湊成10，再加上余下的數，這樣不但快，而且不容易出錯。在學生重復“湊十”的思想時，教師在黑板上板書（如右圖所示）。

模型的建立符合一年級學生的形象思維特征，降低了學生的思考難度。出示題目“9+7”時，學生的思路很清晰：7=1+6，9+1=10 ，10+6=16。反復的練習與反思，使學生在交流解題方法的過程中明確“湊十”的數學思想，并很快掌握了這類計算方法。教師再出示題目“8+6”，學生稍作遷移，就能得出“8+2+4”的思路。

總之，教師在教學中應適時滲透數學思想方法，讓學生在潛移默化中受到數學思想熏陶，有效促進學生數學思維能力的發展，真正提高學生的數學素養，使之終身受益。

（責編 韋 迪）