將轉化思想滲透在數學教學中
汪寶生
[摘 要]轉化不僅是一種數學思想,還是一種重要的解題策略。在小學數學教學中滲透轉化思想,引導學生探究數學知識的內涵,拓寬學生的思路,讓學生感受轉化思想的無窮魅力,有助于“教學有思想,學習有深度”目標的實現。
[關鍵詞]數學思想;轉化;滲透;小學數學
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2017)11-0089-01
數學不僅包括數學知識,還包括數學結論的形成過程和數學思想。小學數學是數學學習的基礎,需要教師有意識地滲透數學思想,引導學生感悟數學的本質。
一、挖掘聯系,自主建構
數學是一門前后聯系非常緊密的學科,教師要理清教材脈絡,對教材結構有清晰的把握,從已有知識引入新知,引導學生尋找學習的突破口,并在原有認知的基礎上得到提升,不斷更新和完善知識框架。
如教學“計算多邊形面積”時,多邊形面積公式的推導是教學的重點和難點,但是其知識結構卻是零散的。如何突破這一弊端呢?切入點就是轉化。
如教學“平行四邊形的面積”時,教師首先引導學生思考如何將平行四邊形轉化為長方形,并引導學生討論為什么要轉化。經歷了知識的推導過程,學生在學習三角形與梯形的面積時,就會主動設法將這些圖形轉化為長方形,以長方形為起點,找出兩者之間的面積關系,便于加深學生對知識的理解。
二、創設情境,深度體驗
依據學生的認知和年齡特點,教師應創設豐富、有效且有趣的情境,激發學生的學習積極性,幫助學生更好地理解知識。在滲透轉化思想的過程中,借助情境將會收獲更好的成果。
如教學“小數乘整數”時,教師創設了購物情境:媽媽買了3千克蘋果,每千克8.6元,應付多少元?根據“單價×數量=總價”,學生能較快列出算式8.6×3。雖然這是第一次系統地學習小數乘整數,但是有購物情境的依托,學生很快就探究出三種不同的計算方法:(1)8.6+8.6+8.6=25.8(元);(2)8.6元=8元6角,8元×3=24元,
6角×3=1元8角,24元+1元8角=25元8角=25.8元;(3)8.6元=86角,86角×3=258角=25.8元。經過計算,學生發現了小數乘法與整數乘法之間的聯系,加深了對算理的理解。此時,教師再引導學生結合計數單位進行理解:8.6表示86個0.1,25.8表示258個0.1。借助積的變化規律,學生總結出小數乘整數的計算規則。
依托生活情境,找準知識間的聯系,利用舊知解決了學生遇到的新問題,豐富對轉化的感知方式,也為后續的學習打下堅實的基礎,轉化思想也隨之潛入學生心中。
三、拓寬思路,培養意識
轉化思想不僅僅局限于化新為舊,還體現在化繁為簡。在解決實際問題的過程中,教師應有意識地引導學生充分利用已有知識和經驗,將復雜轉化為簡單,將未知轉化為已知,不斷豐富學生的解題策略,拓展學生的思維。
如教學“分數的實際應用”時,教師引導學生發現分數和比之間的聯系,探究不同的解題思路。對于“六(2)班有56名學生,其中男生人數是女生人數的3/4。六(2)班男、女生各有多少人?”這道題,除了常規的列方程解答外,教師還可以啟發學生將“男生人數是女生人數的3/4”轉化為“男生人數與女生人數的比為3︰4”,再按比例分配的思路進行解答,從而拓寬學生的解答思路。
又如探究“圓柱體的體積的計算公式”時,教師引導學生將圓柱體轉化為長方體,從而得出圓柱體的體積=底面積×高,其中的底面積是指圓柱體的底面積。在解答“一個圓柱體的底面半徑是4厘米,側面積是37.68平方厘米,體積是多少立方厘米?”這個問題時,常規思路是先算出圓柱體的底面周長,再用“側面積÷底面周長”求出圓柱體的高,然后根據圓柱體的體積公式求出圓柱體的體積。如果在探究圓柱體的體積公式時將圓柱體轉化成“躺”下來的長方體,底面積變成了圓柱體側面積的一半,高是圓柱體的底面半徑,便可得到另一種計算圓柱體積的方法。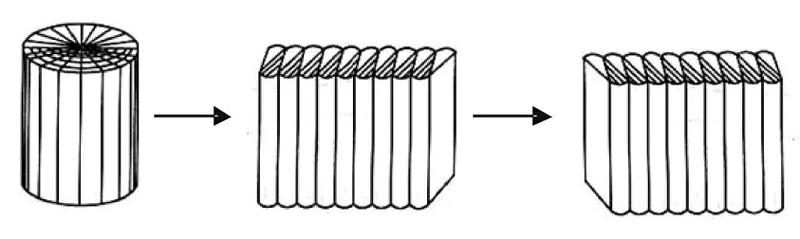
多做類似的訓練,可使學生意識到轉化是解決問題的重要且有效的途徑。在面對棘手的數學問題時,學生就會懂得變通,及時調整思考的方向,形成習慣轉化、善于轉化的意識。
轉化思想存在學習的各個領域,數學教師應當提升自身的轉化意識,提煉教材中的轉化素材,適時滲透轉化策略,使轉化思想根植于學生的腦海中。
(責編 韋 迪)

