給學生一種“不同”的視界
——《(連乘)解決問題》教學
范林偉
【教學內容】
人教版三年級下冊第四單元第52頁。
【教學重點】
會選擇有直接聯系的信息,從不同的角度解決連乘問題。
【教學難點】
建立連乘的數學模型,感悟其數學價值。
【教學過程】
一、在購物情境中提出并解決問題
1.有序呈現條件。
(1)學校要舉辦運動會。王老師想買6箱飲料,每瓶5元。
師:這是一個與購物有關的數學問題。王老師帶了400元錢想一次性買到這些飲料,夠不夠呢?如果你是老師,你覺得這其實是要解決一個什么數學問題?
生:買這些飲料一共要多少錢?
師:現在能解決嗎?為什么?
生:不能,因為還不知道一箱有多少瓶飲料。
(2)每箱有12瓶。
師:現在,你覺得能解決哪些數學問題?
生1:買一箱要多少元?
生2:一共買了多少瓶?
生3:一共要用多少錢?
生4:王老師帶的錢夠嗎?
2.學生獨立解決“一共要用多少錢”,教師指名反饋。
生1:每瓶飲料5元,每箱有12瓶,5×12=60算出買一箱60元。有這樣的6箱,所以再乘 6,60×6=360(元)。
生 2:5×12×6=360(元),我也是先算出一箱多少錢,再算6箱一共要多少錢。
師:為什么第二步還是用乘法?
生:他先算出了一箱要60元,有這樣的6箱,就是求6個60是多少,所以用乘法算。
師:他們是怎么想的,誰還聽懂了?這兩種方法有什么相同點和不同點?
生:他們都是先算出一箱多少錢,再算6箱一共要多少元。不同的是,一個是分步算的,另一個是列綜合算式算的。
教師追問:要求一共用了多少元,先要求什么?
生:先要求出買一箱多少元。
師:如果不這樣想,還可以怎么想?
生1:每箱有12瓶,一共有6箱,12×6=72算出一共要買72瓶,每瓶5元,所以72×5=360(元)。
生2:還可以列綜合算式計算,12×6×5=360(元)。
小結:原來選擇不同的信息進行搭配,就會產生不同的解決方案。
3.強化乘法的意義。
師:如果再買3箱,一共要付多少錢?
生 1:60×3=180(元),360+180=540(元)。
生 2:12×5×9=540(元)。
師:這兩種方法哪種更方便?
【反思:首先將學生置于購物問題之中,迫使學生以主人公的姿態分析、提煉出數學問題,體會沒有直接聯系的信息是無法解決問題的。然后,使學生在討論、分享中理解每步算式的含義,同時溝通與綜合算式之間的聯系。這樣,有利于學生經歷解決問題的基本過程,理解不同的解決思路,體會中間問題的重要性,并初步感受與總價有關的數量關系。最后,組織學生討論“再買3箱”哪個方法更方便,使學生從乘加走向連乘,深化乘法的意義,進一步感受連乘的特征、意義與價值。】
二、從常規思考走向非常規思考
1.有序呈現條件。
(1)學校跑道每圈長400米。小紅每天跑2圈。
(2)她一個星期(7天)跑多少米?
師:[第(1)條]要解決這個問題必須要知道哪些信息?
師:[第(2)條]想一想,你打算怎樣選擇信息?并列式計算。
2.學生獨立計算后,課件出示四種備選方案。
(呈 現 :A.2×7×400、B.400×2×7、C.400×7、D.400×7×2)
師:你是怎樣想的?說說你的想法。
生1:我是第二種方法,400×2先算出每天跑800米,要跑7天,所以還要乘7,算出一共要跑5600米。
生2:我是第一種方法,2×7先算出一周要跑14圈,每圈是400米,就是求14個400是多少,所以還要乘400。
生3:我是第四種方法,400×7×2先假設一天跑一圈的話,7天跑了2800米,實際上一天跑2圈,所以還要乘2。
師:誰聽懂了第四種思考方法,這樣想可以嗎?
(學生四人小組討論、說理與計算,驗證思路與結果的合理性)
3.觀察算式特征,揭示課題。
【反思:讓學生借助跑步情境鞏固新知,在解釋說明算式算理的過程中進一步明確“先求什么,再求什么”,使學生再次體會連乘問題的特征與基本數量關系。并且,實現他們從常規思考向非常規思考的跨越,深刻體會“假設法”的合理性。】
三、學會靈活選擇解決問題的策略
1.依次呈現條件和問題,學生邊看邊編題。
出示線段條:學校為運動員們準備了三種水果。蘋果有12千克,橘子質量是蘋果的3倍,香蕉的質量是橘子的4倍。香蕉一共多少千克?
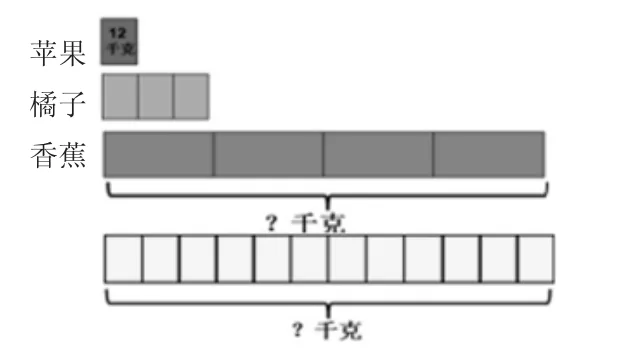
2.學生獨立解決問題,指名反饋。
生 1:12×3×4,12×3 先算出橘子的質量,因為香蕉的質量是橘子的4倍,所以還要乘4,就能算出香蕉的質量了。
生 2:3×4=12,12×12=144(千克)。
(很多學生看不懂,教師組織學生小組討論)
生3:(邊說邊指)他是這樣想的,橘子是蘋果的3倍,橘子就可以看成這樣的3份,那么,香蕉就有這樣的12份,也就是香蕉的質量就是蘋果的12倍了,所以可以用12×12算出香蕉的質量。
(課件直觀支持,幫助學生深化理解)
【反思:大多數學生能解釋說明“12×3×4”的方法,但很少有學生能說清“3×4×12”的思維過程。讓學生借助線段條來分析問題,發現“3×4”就是先求出香蕉是蘋果的12倍,再求出香蕉的數量。通過這樣的變式,既強化了學生對知識的理解,又幫助學生形成了一種新的思維方式,即遇到困難時可以嘗試借助幾何直觀來解決問題的意識和能力。這樣,有利于學生充分感受幾何直觀對于分析問題、明確數量關系、發現思路和解決問題的重要性。同時,也為學生后續學習小數、分數的連乘問題埋下了解題策略的種子。】
四、學會轉換觀察角度進行思考
師:其實,生活中還有很多類似的數學問題,我們一起來看:
練習1:根據算式4×6×8,你知道小明是站在哪個方向(正面、左面、上面)觀察這盒積木的嗎?誰來演示一下?你還能從別的角度觀察,計算出它里面一共有多少個小正方體嗎?

練習2:東南大廈有12層,每層有4個窗戶。每個窗戶安裝6塊玻璃,一共要安裝多少塊玻璃?你有幾種解決問題的方法?
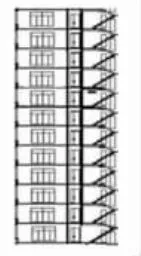
(學生計算并說理)
【反思:通過轉換觀察的視角使學生進一步感受選擇不同的信息會產生不同的解決問題的方法。這樣,既鞏固了用連乘解決問題的知識,又強化了用假設法“6×12×4”來解決問題的合理性,同時還發展了學生的直覺思維,拓展了連乘模型的應用領域。】

