“以學為中心”的有效數學課堂的構建
——賁友林老師《圓的認識》教學片斷賞析

徐黎明

“以學為中心”的課堂，就是以生為本，以學為主的課堂，是學生通過自主學習、小組合作等學習方式進行問題探究，是教師組織指導，有效引領，高效達標的課堂。蘇霍姆林斯基說過：“在人的心靈深處都有一種根深蒂固的需要，就是希望自己是一個發現者、研究者、探索者。”

【片斷一】引入：初步感知圓

師：關于圓，知道了什么？

（學生思考后，交流匯報）

生：圓和多邊形都是平面圖形。

生：圓是一種幾何圖形，它有半徑、直徑、圓心。

生：圓有無數條半徑、直徑。

生：圓沒有直線，只有曲線。

生：圓上的點到圓心距離相等。

生：圓有無數條對稱軸。

生：圓上任意兩點之間的部分叫弧。

生：畫圓要找圓心。

【賞析：上課伊始，賁老師請聽課老師隨機抽出一個學號30號，由學號30號學生來請其他同學回答問題。賁老師主動把課堂讓給學生，讓學生真正成為學習的主人。賁老師精心設計問題，在學生的回答中，可以初步知道學生對圓有哪些了解。從學生的交流中，可以看出學生課前的預習很重要。有效的預習使學生明白新課要學習的知識中有哪些知識點自己還不是很清楚，能夠提出什么問題。導入新課時，賁老師放手讓學生來請學生回答，學生在輕松的氛圍中展開學習。】

【片斷二】操作：畫圓的步驟

師：認識了圓，會用圓規畫圓的舉手？

教師請一名學生用圓規試著畫出一個圓。

師：要注意什么？大家一邊看一邊想。

生：針尖固定的沒有動。

師：手抓圓規的頭，有頭就有腳。你能看到不動的地方嗎？什么不動？

師：半徑在哪里？

生：兩腳之間的距離是半徑，這個長度不能動。

【賞析：在教學用圓規畫圓時，賁老師先了解班級里有哪些學生已經會用圓規畫圓，同時請學號是8號的學生現場展示用圓規畫圓。其余學生在看8號同學畫圓時通過觀察發現針尖是一個固定的點，這個點位置沒有發生變化。學生找出了“定點”這一步后，接著讓學生在交流中發現圓規兩腳之間的距離也沒有變化。用手抓住圓規的“頭”，旋轉一周就能畫出一個完整的圓。學生在自主探索中知道畫圓的步驟：定點、定長、旋轉。賁老師讓學生以研究的方式來學習數學，讓教師的教服務于學生的學，進而體現了“以學為中心”的教學理念。】

【片斷三】探究：觸摸圓特征

師：誰能找出所畫圓的圓心？

生：針尖上的那一點，就是圓心O。

（學生畫出一條半徑）

師：半徑是什么？

生：半徑是一條線段。

師：線段有兩個端點，圓的直徑是什么？

生：直徑也是一條線段。

師：直徑為什么不是直線？在圓上面從哪到哪是直徑？哪兩個端點？有補充嗎？

教師用直尺在圓上進行擺放。這樣畫是直徑嗎？

生：要經過這個圓的圓心。

師：現在畫了幾條半徑？

生：3條半徑。

生：1條半徑。

生：我認為是3條半徑，1條直徑可以分成2條半徑。

師：還可以畫多少條半徑和多少條直徑？

生：可以畫無數條半徑和直徑，而且直徑的長度是半徑的2倍，半徑長度是直徑的一半。

師：圓心寫在哪里？

生：圓心在圓的中心，就是畫圓時，針尖所在的點。

師：定長是什么？定長3cm，這3cm指的是什么？

生：是指畫的圓半徑是3cm。

師：我要畫一個圓半徑2cm，圓規兩腳間的距離是多少？

生：2cm。

師：誰能說一說，什么是圓的對稱軸？

生：直徑所在的直線就是對稱軸。

【賞析：在學習圓的各部分名稱時，先讓學生找出所畫圓的圓心，就是畫圓時針尖固定的一點，可以用字母O表示。賁老師讓學生在圓上試著畫出一些半徑。在交流中知道半徑是連接圓心到圓上任意一點的線段。在畫半徑時，有名學生畫出的是直徑，是通過圓心并且兩端都在圓上的線段。畫圓的直徑時，賁老師用直尺放在圓上，上下移動直尺時，讓學生判斷畫出的線段是不是直徑。學生根據是否通過圓心來判斷直尺所在的線段是不是直徑。在同一圓內畫了一條半徑和一條直徑后，賁老師問學生有幾條半徑，這是一個看似簡單，其實蘊含著半徑與直徑之間長度關系的問題。一條直徑可以分成兩條半徑，這樣半徑與直徑的關系就呈現出來。在圓中有無數條半徑，有無數條直徑。畫圓時定點后就要定長，定長就是確定圓規兩腳間的距離，即確定圓的半徑長度。圓是軸對稱圖形，有無數條對稱軸。對稱軸是一條直線，圓的對稱軸是圓的直徑所在的直線，就是它的對稱軸。學生明白了圓的直徑有無數條，圓的對稱軸也有無數條。】

【片斷四】反饋：按要求畫圓

畫圓：1.點A在圓上。

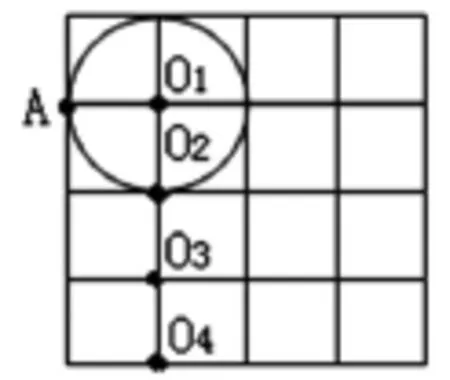
生：畫出如圖中的圓O1。

師：還有不同的畫法嗎？只要標出圓心，不用畫出來。

生：接著又標出了圓心O2、O3、O4。

師：這三個圓大小一樣嗎？

生：大小不一樣。

師：由此可以看出哪個圓最大？圓的大小由誰來決定？

生：圓的大小由半徑（或是直徑）來決定。

師：圓的位置又由誰來決定呢？

生：圓心。

畫圓：2.點A、B都在圓上。

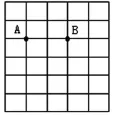
畫圓：3.點 A、B、C 都在圓上，先找出點C，再畫出圓。

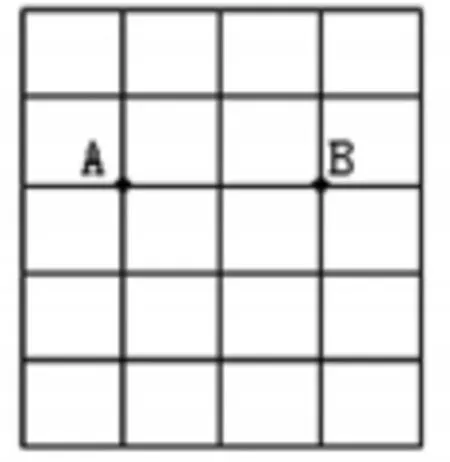
【賞析：在練習環節，賁老師精心設計了一組題，不但有效鞏固了學生所學的知識，而且提升了學生的思維能力。賁老師設計的這組題，由淺入深，層層推進。問題一先讓學生畫出有一個已知點在圓上的圓，學生根據要求可以畫出多個符合要求的圓，畫出的不同圓的大小也是不一樣的。賁老師讓學生回答圓的大小由什么決定，學生在自己的畫圖中，可以感知到圓的大小是由圓的半徑來決定的。問題二要求畫出點A、B都在圓上，學生在畫出不同的圓進行觀察時會發現要使A、B兩點都在圓上，這些圓心都在線段AB的對稱軸上面。問題三的設計，進一步提升學生的思維能力。學生需要綜合運用到所學圓的知識來進行解答。】