無黏結支撐的軌道板板角離縫研究
趙磊 孫璐 孫偉 趙國堂
摘要:為研究溫度影響下的高速鐵路無砟軌道板翹曲變形和變化規律,基于最小勢能原理,利用傅里葉級數模擬軌道板翹曲過程的翹曲變形,對負溫度梯度引起的板角離縫進行研究。利用京滬高速鐵路CRTSⅡ型軌道板現場實測的板角翹曲數據,驗證本文用于計算軌道結構翹曲變形的基于最小勢能原理的計算方法,分析溫度梯度影響下的軌道板翹曲規律。對比結果表明:新方法得到的計算結果和實測數據得到的數據吻合較好,驗證了該方法的可靠性。研究結果表明:板端翹曲變形與溫度梯度變化成正相關性,增大地基系數可以有效地減小溫度引起的軌道板板端翹曲變形。
關鍵詞:軌道結構;板角離縫;勢能方程;傅里葉級數;擬Newton迭代
中圖分類號:U238 文獻標識碼:A
與傳統有砟軌道相比,高速鐵路無砟軌道具有乘坐舒適、方便快捷、運輸能力強等優勢,因此成為鐵路客運專線發展的必然選擇。隨著高速鐵路的迅速發展,板中隆起、板端翹曲引起的平順性衰減嚴重地影響著高速鐵路運行的安全。太陽照射會使軌道板“上熱下冷”,強降溫等會造成軌道板表面的溫度驟然降低,使得軌道板“上冷下熱”。這種在軌道板厚度方向上產生的溫度梯度荷載會導致軌道板產生周期性的翹曲變形,對設計使用壽命要求不小于60年的無砟軌道結構,需考慮溫度變形的長期疲勞效應。
國內外學者對水泥路面混凝土板的溫度翹曲變形研究較早。Choubane等考慮了非線性溫度梯度對水泥鋪面的影響,采用二次方程表述非線性溫度曲線,研究了非線性溫度梯度對溫度應力和變形的影響。William等通過建立精細化的具有傳力桿的混凝土路面模型,研究了路面溫度應力及溫度變形。Belshe等通過測量混凝土路面路表和板底溫度變化,對混凝土路面溫度翹曲問題進行了研究,通過數值模擬對影響鋪面垂向位移的因素進行了分析。Nam等通過測量1 d中機場鋪面的撓度變化,對機場鋪面溫度翹曲問題進行了研究,通過數值模擬對影響鋪面垂向位移的因素進行了分析。
隨著無砟軌道的廣泛應用,國內學者和機構對無砟軌道結構的翹曲變形也進行了深入研究。王繼軍等利用有限單元法研究了單元板式無砟軌道板溫度翹曲變形問題。劉鈺等通過在不同氣候條件下現場觀測CRTSⅡ軌道板溫度,得到實測的軌道板溫度梯度,建立了軌道結構力學有限元模型,計算軌道板在實測溫度梯度作用下的溫度翹曲變形。盧煒針對嚴寒地區哈大客運專線上CRTSⅠ型軌道板與充填層砂漿四角離縫的實測結果,探討CRTSⅠ型軌道板四角離縫成因,提出了減小離縫的施工應對措施。王雪松等通過建立CRTSⅡ的力學模型,分析軌道板的不同負溫度梯度,以及軌道板與砂漿層之間不同的黏結條件對軌道系統受力與變形的影響。戴公連等通過對客運專線曲線段簡支梁橋上縱連板式無砟軌道結構溫度場的連續觀測,研究了秋季多種天氣情況下曲線橋上無砟軌道溫度場的時變規律。這些成果對分析與了解無砟軌道結構的翹曲變形有極大幫助,但對無砟軌道結構翹曲變形的研究多停留在觀測層面上,對軌道板的溫度翹曲變形理論研究較少,因此,對無砟軌道結構翹曲變形規律開展研究具有重要的意義。
綜上所述,現有無砟軌道結構溫度翹曲變形的研究方法,有解析法和有限元法兩種。解析法多采用威斯特卡德理論,假設板與地基始終保持接觸,無空隙,推演了板由于地基約束而產生的翹曲變形;有限元法通過建立無砟軌道結構模型,設置相應的材料熱力學參數和邊界條件,得到結構的變形與內力。然而這兩種方法各有缺點:威斯特卡德解假設板與地基始終保持接觸,無空隙,與無砟軌道溫度翹曲變形后產生離縫的實際狀況不符。有限元方法,建模方法不統一,結果受模型尺寸、網格大小、邊界條件影響較大,不利于工程設計。本文基于能量法的軌道板翹曲變形研究,采用傅里葉級數來模擬軌道板翹曲過程中的翹曲曲線,根據擬Newton迭代算法求得軌道板翹曲曲線方程。文中對不同溫度梯度和不同地基系數下軌道板的翹曲變形量進行了分析,探討了降低板角離縫的方法。
1軌道板翹曲變形計算模型
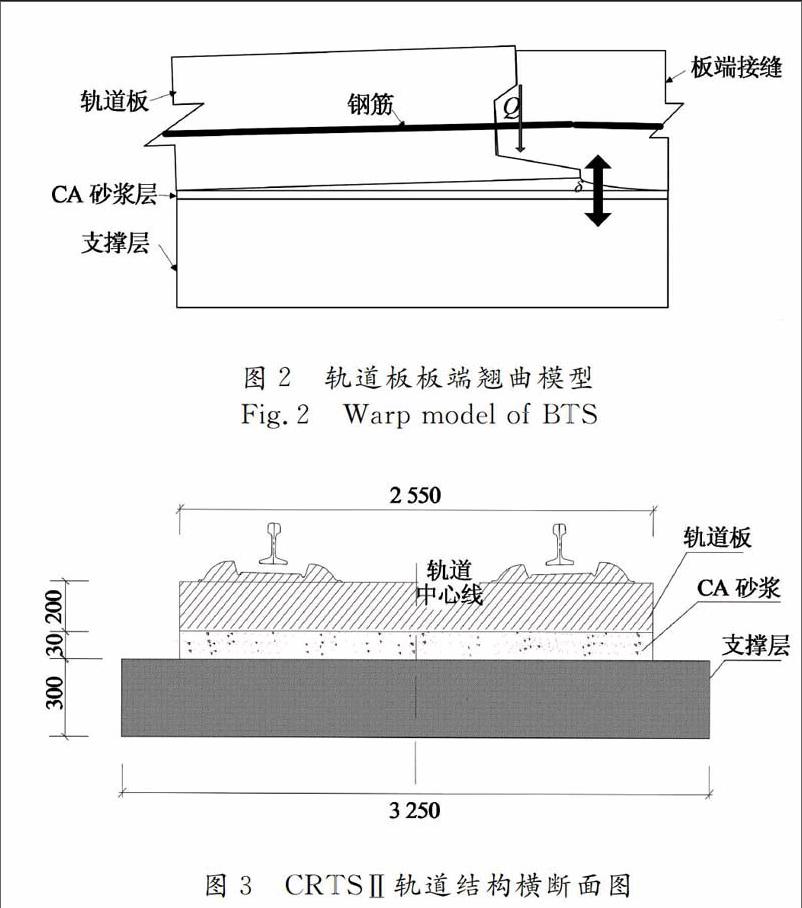
傳導、對流、熱輻射是組成無砟軌道結構熱量平衡的3種基本傳熱方式。無砟軌道通過熱輻射和對流過程獲得熱量,以熱傳導的形式在無砟軌道結構內部傳遞,軌道結構熱交換過程如圖1所示。當板內溫度梯度較大時,無砟軌道板會發生翹曲變形。當翹曲變形受重力作用、砂漿層的黏結作用以及鋼軌和扣件系統的約束作用時,板內會產生翹曲應力,如圖2所示。溫度應力是導致無砟軌道結構早期開裂的重要因素。圖3所示為典型無砟軌道結構橫斷面圖,結構自上向下分別為軌道板、砂漿層和支撐層。
2基于能量法的軌道板翹曲變形研究
無砟軌道結構隨溫度變化產生翹曲變形,導致與支撐層連接處產生離縫,引起軌道平順性衰減,在高速列車動荷載作用下,離縫處的軌道板與基礎反復彎曲變形,造成板端破碎以及支撐層剝離和破碎,形成安全隱患。軌道板的翹曲變形分為2種:一種是軌道板表面溫度高于內部溫度,造成“上熱下冷”的情況,此時軌道板中部拱起,板角下沉。另一種是軌道板表面的溫度驟然降低,使得軌道板“上冷下熱”,此時產生如圖2所示的板角上翹,板中下沉。圖4所示為軌道板微分單元受力模型,軌道板在線性溫度梯度作用下,產生如圖所示的溫度應力。當板表面溫度高于板底溫度時,板中部拱起,此時受板的自重、鋼軌和扣件系統的約束作用,拱起量較小;當板表面溫度低于板底溫度時,板角由于后澆帶的存在,容易在荷載和溫度作用下產生應力集中,后澆帶開裂,板角翹曲量大,形成表面裂縫。裂縫的張開寬度與結構的耐久性有密切關系,裂縫開裂寬度過大,會使鋼筋腐蝕加劇,結構加速破壞,板角翹曲比板中拱起更為不利。
無砟軌道為曝露于大氣環境下的條帶狀結構物,CRTSⅡ型軌道板采用了預應力筋低放用于抵抗板檐上翹的設計理念,橫向翹曲量小,本文研究中忽略軌道板的橫向彎曲,將軌道板簡化為梁構件。將軌道板下部支撐結構假設為溫克勒地基,即支撐剛度簡化為一系列獨立的線性彈簧。板端在翹曲過程中受到板端接縫的約束作用,該約束作用以接縫嵌鎖模量(modulus of interlocking joint)表征,該模量值是集料尺寸、接縫開裂寬度、接縫接觸面積的函數。
采用傅里葉級數來模擬軌道板翹曲過程中的翹曲曲線,并假設軌道板兩端的翹曲值相等。考慮板端的邊界條件,同時兼顧級數可導性,可將軌道板翹曲曲線用式(1)表示。
(1)式中:ω0,ω1,…,ωn為撓曲線的待定系數;l為軌道板計算長度;n為級數計算次數。
軌道板的彎曲變形能U1為:
(2)式中:E為軌道板彈性模量;J為軌道板截面慣性矩;L為軌道板計算長度。
軌道板翹曲,軌道板與支撐結構部分脫離,脫離點在計算坐標系(如圖1所示)的坐標分別為a和6,此時軌道板的彈性支撐變形能U2為:
(3)式中:k為支撐軌道板的彈性地基系數;B為軌道板寬度。
板端在翹曲過程中受到板端接縫的約束作用(如圖2所示)的變形能U3為:
(4)式中:ks為接縫嵌鎖模量。
溫度梯度做功V:
(5)
由能量法計算獲得的傅里葉級數的系數衰減迅速,通過計算分析可知(見表1),當取到級數的第二項時,其系數已經非常小,基本可以忽略。為簡化計算,取傅里葉級數的前兩項,即
(6)
(7)
(8)
(9)
(10)
軌道板的真實位移函數ω應該使總勢能Ⅱ為最小值,即叫應該使Ⅱ的一階變分為零,即
(11)
將式(4)(7)(8)(9)代入式(10),總勢能函數Ⅱ將變成ω0,ω1,ω2的函數,根據最小勢能原理,這些待定常數應使總勢能函數Ⅱ為極值,因此必須有:
(12)
同時,軌道板翹曲脫離點a和b應滿足翹曲曲線方程,即:
(13)
(14)
式(12)(13)(14)是5個待定常數的非線性方程組,本文求解采用擬Newton迭代算法(如圖5所示),即可解出未知數,矩陣Ak+1關于點{x}k及{x}k+1具有“差商”性質。
3軌道板翹曲變形計算分析
3.1計算方法驗證
京滬高鐵鋪設CRTSⅡ型軌道板時,在某路段對3塊相連軌道板的周圍空氣溫度、軌道板溫度、翹曲變形值進行了實測。為測量軌道翹曲變形,用千分表觀測,將6個千分表分別布置在板角和縱向板邊緣中部。
為了驗證本文算法的正確性,取標準CRTSⅡ軌道板進行分析,軌道板寬度為2.55 m,長度為6.45 m,厚度為0.2 m,泊松比μ為0.15,軌道板彈性模量E為3.55×104MPa,膨脹系數αE為1×10-5,地基反應模量為20 MPa/m,接縫嵌鎖模量為0。7 MPa/m。用本文的方法計算軌道板角翹曲變形并與實測數據進行對比,如圖6所示,可見本文的計算方法能夠比較準確地用于軌道結構翹曲變形計算。圖6(b)中,實測板角翹曲變形較計算值略大,原因是計算模型將軌道板簡化為一維模型,未考慮另一方向翹曲變形對該方向的影響,同時由于計算過程中將溫度梯度進行線性分布假設,未考慮非線性溫度對軌道板的影響。然而計算與實測的變形差在溫度梯度40℃/m僅有0.07 mm,對比結果進一步證明了本文關于軌道板翹曲變形計算方法的準確性和有效性。
3.2溫度梯度影響下的軌道板翹曲規律
為了分析溫度梯度對軌道板端部翹曲的影響,選取了6組不同的溫度梯度進行分析,軌道板上下表面溫差變化范圍從2℃到12℃,變化幅度為2℃,見表1。由表1可知,當軌道板上下表面溫差為2℃(溫度梯度10℃/m)時,板端翹曲位移為0.198mm,板中心下沉量為0.226 mm;當軌道板上下表面溫差為8℃(溫度梯度40℃/m)時,板端翹曲位移為0.515 mm,約為溫度梯度20℃/m時板端翹曲位移的2.6倍,板中心下沉量為0.553 mm,約為溫度梯度10℃/m時板中心下沉量的2.4倍;當軌道板上下表面溫差為12℃(溫度梯度60℃/m)時,板端翹曲位移為0.686 mm,約為溫度梯度10℃/m時板端翹曲位移的3.5倍,板中心下沉量為0.737mm,約為溫度梯度10℃/m時板中心下沉量的3.3倍。
由圖7和圖8可知,隨著軌道板溫度梯度的變化,軌道板板端翹曲變形和板中心下沉量也相應變化。隨著軌道板負溫度梯度增大,板端翹曲變形增大,板中心下沉量也相應增加,與溫度梯度變化成正相關性;軌道板板端翹曲變化與板中心下沉量變化和溫度梯度變化均近似直線關系;在同一溫度梯度時,板中心下沉量比板端翹曲變形量大。
3.3地基系數影響下的軌道板翹曲規律
為了研究地基系數對軌道板端部翹曲的影響,選取了5組不同的地基系數進行分析,地基系數變化范圍為2×105~2×109Pa/m,見表2。
由表2可知,當地基系數為0.2 MPa/m時,板端翹曲位移為0.376 mm,相應板中心的下沉量為0.403 mm;當地基系數增大為20 MPa/m時,板端翹曲位移為0.343 mm,約為地基系數為0.2 MPa/m時板端翹曲位移的0.9倍,板中心的下沉量為0.368 mm,約為地基系數為0.2 MPa/m時板中心下沉量的0.92倍;當地基系數為2 000 MPa/m時,板端翹曲位移為0.020 1Tim,約為地基系數為0.2MPa/m時板端翹曲位移的0.05倍,板中心的下沉量為0.028 mm,約為地基系數為0.2 MPa/m時板中心下沉量的0.07倍。
由圖9和圖10可知,增大地基系數可以有效地減小溫度引起的軌道板板端翹曲變形。隨著地基反應模量增大,板端翹曲變形減小,板中心下沉量也相應減小,與地基反應模量變化成負相關性;軌道板板端翹曲變化和板中心下沉量變化均與地基反應模量變化呈非線性關系,突變點在地基反應模量為200MPa/m處。
為了減小負溫度梯度引起的軌道板板端翹曲變形,軌道板下部結構應采用剛度較大的支撐層,然而軌道結構動力響應會隨著彈性地基剛度增大而增大,因此需要結合軌道結構動力分析選擇合理的地基剛度。
4結論
1)本文基于最小勢能原理,利用傅里葉級數模擬軌道板翹曲過程的翹曲變形,對負溫度梯度引起的板角離縫進行研究,根據擬Newton迭代算法求得軌道板翹曲變形以及翹曲曲線方程。該方法具有準確簡單的特點,可以用于工程設計。
2)隨著軌道板負溫度梯度增大,板端翹曲變形增大,板中心下沉量也相應增加,與溫度梯度變化成正相關性;軌道板板端翹曲變化與板中心下沉量變化與溫度梯度變化均近似直線關系;在同一溫度梯度時,板中心下沉量比板端翹曲變形量大。
3)增大地基系數可以有效地減小溫度引起的軌道板板端翹曲變形。隨著地基反應模量增大,板端翹曲變形減小,板中心下沉量也相應減小,與地基反應模量變化成負相關性。
4)為了減小負溫度梯度引起的軌道板板端翹曲變形,軌道板下部結構應采用較大的彈性地基系數,然而軌道結構動力響應會隨著彈性地基系數增大而增大,因此需要結合軌道結構動力分析選擇合理的地基系數。
5)計算模型將軌道板簡化為一維模型,未考慮另一方向翹曲變形對該方向的影響,同時由于計算過程中將溫度梯度進行線性分布假設,未考慮非線性溫度對軌道板的影響,這是以后工作中要考慮的內容。