后向平滑與抗差估計融合的SRCKF濾波

孫 鵬，趙長勝，譚興龍，張立凱

(江蘇師范大學地理測繪與城鄉規劃學院，江蘇 徐州 221116)

后向平滑與抗差估計融合的SRCKF濾波

孫 鵬，趙長勝，譚興龍，張立凱

(江蘇師范大學地理測繪與城鄉規劃學院，江蘇 徐州 221116)

將后向平滑平方根容積卡爾曼濾波用于GPS動態單點定位數據處理，并探討了粗差對后向平滑濾波的影響。借鑒經典卡爾曼濾波抗差估計思想，給出平方根容積卡爾曼濾波的抗差算法以抵抗量測粗差，而當判斷不含粗差時使用后向平滑算法，在有效提高濾波精度的同時避免了抗差濾波對每個歷元都需進行迭代運算。實測GPS動態數據驗證了算法的有效性。

非線性濾波；平方根容積卡爾曼濾波；抗差濾波；后向平滑

擴展卡爾曼濾波(EKF)、無跡卡爾曼濾波(UKF)及粒子濾波(PF)是常用的非線性濾波算法[1]。EKF存在線性化誤差，且常難以獲得雅可比矩陣求導[2]，但在單點定位中，觀測函數非強非線性函數，故常采用EKF進行處理[3-4]。UKF無需線性化，處理強非線性系統時精度明顯優于EKF[5]，但不適當的采樣策略和參數選取可能導致UKF濾波發散[6]。PF則存在計算量大、粒子退化等問題[7-8]。容積卡爾曼濾波(CKF)[9-10]采用基于三階球面-徑向變換的容積準則計算高斯加權積分近似值，數學推導過程嚴格，在維數較高時也可取得良好的濾波效果[11]。本文將一種后向平滑平方根容積卡爾曼濾波(BS-SRCKF)用于單點定位，給出SRCKF的抗差算法，并探討了抗差算法與后向平滑的融合。

1 平方根容積卡爾曼濾波(SRCKF)

計算機舍入誤差可能導致協方差陣失去對稱正定性，導致濾波失敗，而平方根容積卡爾曼濾波只計算并傳遞協方差陣平方根因子，在提高數值穩定性的同時減小了計算量[12]。當系統狀態為n維時，三階CKF取2n個容積點用于積分近似值的計算。設有離散非線性系統

(1)

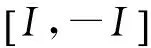
(2)

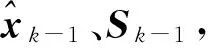
1.1 時間更新

求解、更新容積點

(3)

狀態預測值及其協方差陣平方根因子

(4)

tria()表示一種三角化運算[9]，其中

1.2 量測更新

求并更新容積點

(5)

求預測觀測值、新息協方差陣的平方根因子與互協方差陣

(6)

式中

計算增益矩陣，更新狀態及其協方差陣平方根因子

(7)

2 后向平滑平方根容積卡爾曼濾波(BS-SRCKF)

后向平滑濾波可有效提升濾波精度，在平方根容積卡爾曼濾波下，其流程可表示為

(1) 用式(3)—式(7)進行前向濾波得k時刻濾波值。

(2) 按下式獲取k-1時刻狀態平滑值[13]

(8)

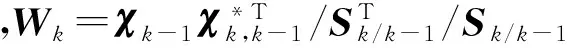
(3) 將后向平滑值作為k時刻初值再次按式(3)—式(7)前向濾波。

3 抗差平方根容積卡爾曼濾波(R-SRCKF)

當預測信息準確時，粗差將直接反映在預測殘差中。通過預測殘差及其協方差陣可構建抗差因子，若存在粗差，放大該觀測值的噪聲協方差以降低該觀測值在狀態估值計算中的權重，即可抵抗粗差影響。

k時刻預測殘差及其協方差陣為

(9)

(10)

則參考Huber法可求得抗差因子[14]

(11)

式中，c為閾值，可取為c=1.0～1.5，當標準化殘差大于c時，認為該觀測值含粗差。c的取值越小，對粗差的判斷越為嚴格。求得抗差因子后，膨脹量測噪聲協方差

(12)

在非對角線上，按雙因子等價協方差模型取

(13)

以新的量測噪聲協方差陣按式(6)、式(7)求得抗差濾波值及其協方差陣，并對量測更新過程進行迭代直至收斂。

4 帶抗差估計的后向平滑平方根容積卡爾曼濾波(BS-R-SRCKF)

后向平滑濾波采用k時刻濾波結果對k-1時刻濾波結果進行平滑。由式(8)可知，若k時刻存在量測粗差，則k時刻濾波值將不準確，進而后向平滑值，亦即第二次前向濾波的初值也將受到粗差影響，可見，當粗差存在時，BS-SRCKF相比SRCKF受粗差影響更大。同時，單純使用抗差濾波處理粗差需要進行迭代求解，這將增加計算負擔。本文在平方根容積濾波下將后向平滑算法與抗差濾波融合(如圖1所示)，在判定觀測值含有粗差時迭代求解抗差濾波值，否則使用后向平滑算法提高濾波精度。

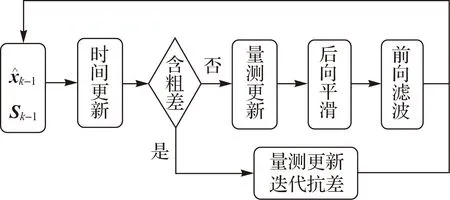
圖1 后向平滑與抗差估計融合的SRCKF流程

5 算 例

取一航攝飛機的一段GPS觀測數據進行濾波解算，采用雙頻消電離層組合偽距，并改正對流層延遲誤差。狀態參數取

偽距量測噪聲方差初值取1 m2。系統噪聲協方差陣Q取

Q=diag([0.09 0.09 0.09 9 0.09 0.09 0.09 9])

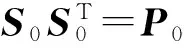
P0=diag([5005005001000100100100100])

分別使用SRCKF和BS-SRCKF進行濾波，以CSRS精密單點定位在線處理輸出值為參考，在WGS-84坐標系下兩種濾波誤差如圖2所示。

現每隔50歷元在其中一顆衛星的組合偽距上加50 m粗差，分別使用BS- SRCKF、BS-R-SRCKF進行濾波，所得結果如圖3所示。

表1為各方案誤差的均方根誤差。

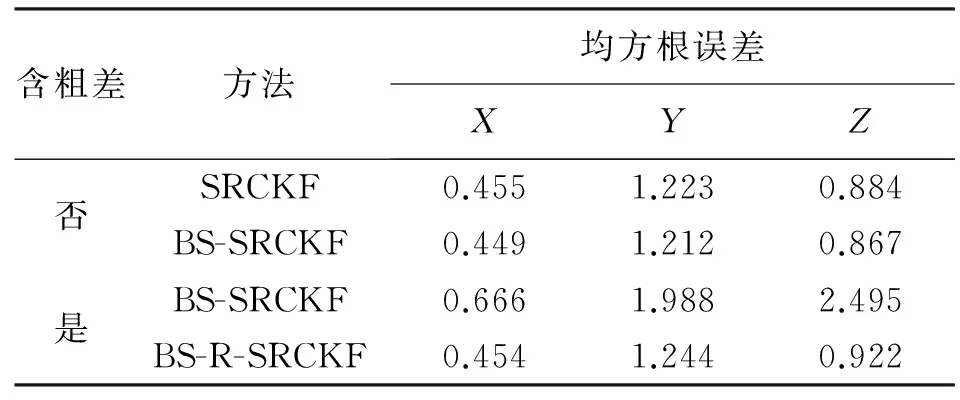
表1 各方案均方根誤差 m

濾波結果表明，后向平滑算法可以有效提高濾波精度，但當量測值含有粗差時，粗差對濾波的影響明顯，而融合抗差估計的后向平滑可有效抵抗粗差、提高濾波的精度。

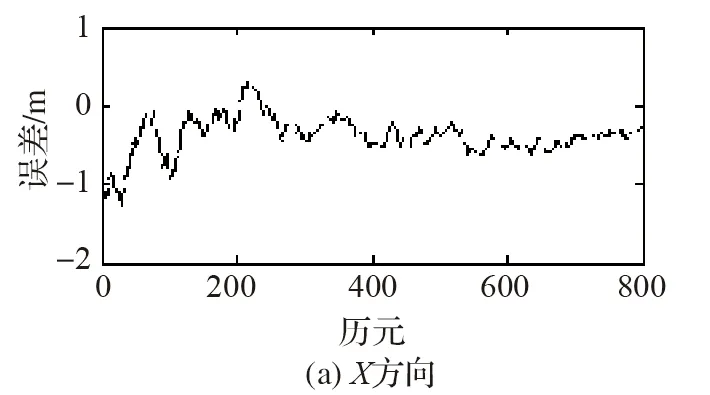
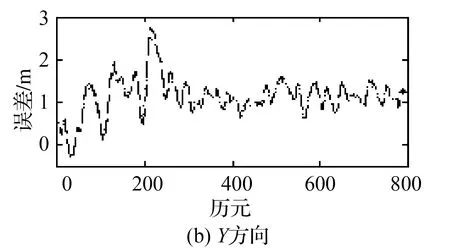
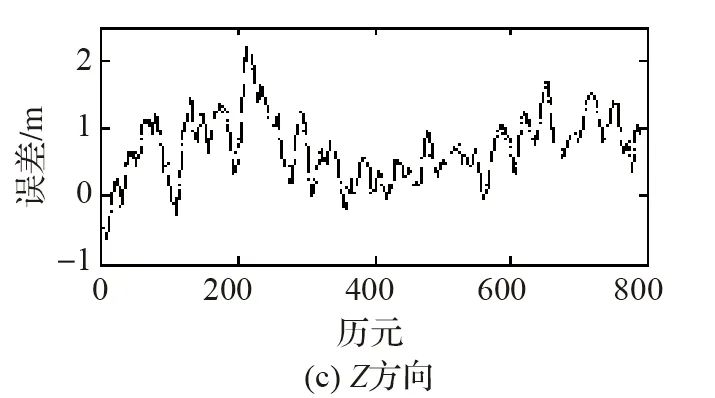
---表示SRCKF，…表示 BS-SRCKF圖2 SRCKF與BS-SRCKF濾波結果

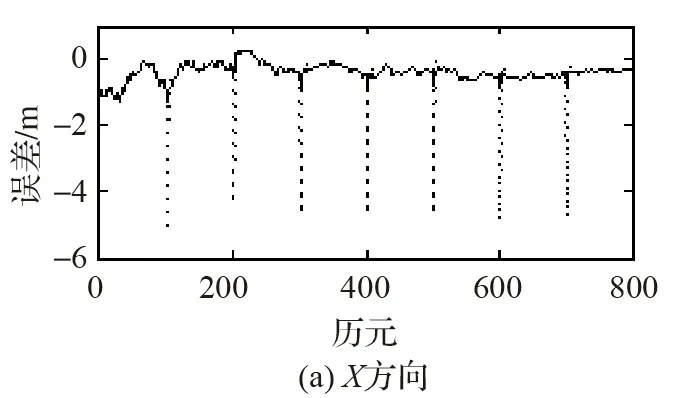
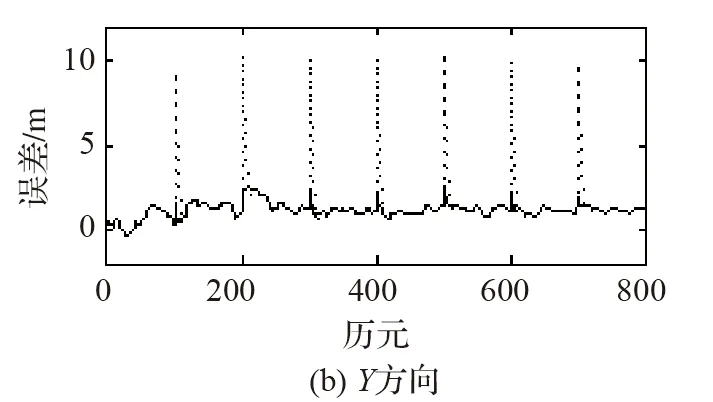
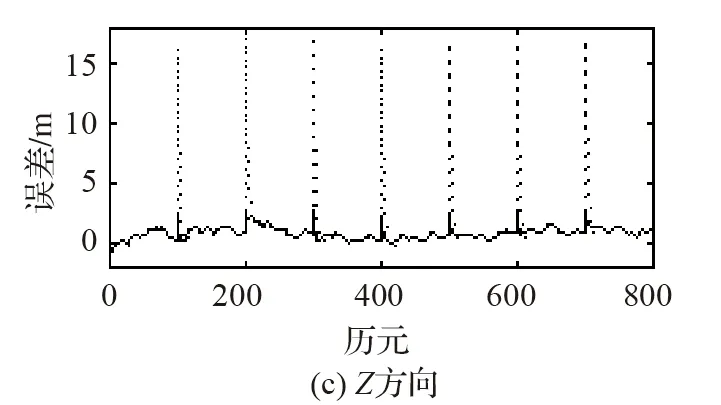
…為BS- SRCKF，—為BS-R-SRCKF圖3 BS-SRCKF與BS-R-SRCKF濾波結果

6 結 語

本文將后向平滑平方根容積卡爾曼濾波用于動態單點定位數據處理，針對粗差對后向平滑濾波的影響，給出了平方根容積卡爾曼濾波下的抗差因子取值。將后向平滑與抗差估計融合，當觀測值含有粗差時進行抗差迭代，當不含粗差時使用后向平滑濾波，提高濾波精度的同時避免抗差濾波每個歷元都迭代帶來的計算量增大問題。實測GPS動態數據的計算結果表明，后向平滑可有效提高濾波精度，與抗差估計的融合也切實可行。

[1] 趙長勝.測量數據處理研究[M].北京：測繪出版社，2013.

[2] 譚興龍,王堅,趙長勝. 神經網絡輔助的GPS/INS組合導航自適應UKF算法[J]. 測繪學報,2015,44(4):384-391.

[3] 祁芳. 卡爾曼濾波算法在GPS非差相位精密單點定位中的應用研究[D].武漢：武漢大學,2003.

[4] 王堅,王金嶺,高井祥. 基于抗差EKF的GNSS導航模型研究[J]. 中國礦業大學學報,2008,37(4):473-477.

[5] 吳江飛,雷輝. 星載GPS衛星定軌的UKF-EKF算法[J]. 測繪學報，2014,43(5):446-451.

[6] 王小旭,潘泉,黃鶴,等. 非線性系統確定采樣型濾波算法綜述[J]. 控制與決策，2012,27(6):801-812.

[7] 聶建亮,楊元喜,吳富梅. 一種基于改進粒子濾波的動態精密單點定位算法[J]. 測繪學報,2010,39(4):338-343.

[8] 薛長虎,聶桂根,汪晶. 擴展卡爾曼濾波與粒子濾波性能對比[J]. 測繪通報,2016(4):10-14.

[9] ARASARATNAM I, HAYKIN S. Cubature Kalman Filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[10] ARASARATNAM I. Cubature Kalman Filtering: Theory & Applications[D].Hamilton：McMaster University, 2009.

[11] 唐李軍. Cubature卡爾曼濾波及其在導航中的應用研究[D].哈爾濱：哈爾濱工程大學,2012.

[12] 郝燕玲,楊峻巍,陳亮,等 平方根容積卡爾曼濾波器[J]. 彈箭與制導學報,2012,32(2):169-172.

[13] 湯霞清,黃湘遠,武萌,等. 平方根形式的CKF/后向平滑非線性濾波研究[J]. 裝甲兵工程學院學報,2015(2):65-69.

[14] 楊元喜.自適應動態導航定位[M].北京：測繪出版社，2006.

[15] 高為廣. 自適應融合導航理論與方法及其在GPS和INS中的應用[D].鄭州：信息工程大學,2005.

Square-root Cubature Kalman Filter with Backward-smoothing and Robust Estimation

SUN Peng，ZHAO Changsheng，TAN Xinglong， ZHANG Likai

(School of Geodesy and Geomatics, Jiangsu Normal University, Xuzhou 221116， China)

Backward-smoothing square-root cubature Kalman filter(BS-SRCKF) is used to caculate observation data of GPS dynamic single point positioning,and the gross errors’ bad influence on backward-smoothing filter is analyzed in this article. In order to reduce gross errors’ impacts, robust SRCKF is put forward referring to robust Kalman filter. And when coarse errors don’t exist,backward-smoothing filter can be used to improve the precision of the results and avoid iterative computation if using robust filter each epoch.Measured data is adopted to prove that the algorithm is effective.

nonlinear filtering; SRCKF; robust filter; backward smoothing

孫鵬，趙長勝，譚興龍，等.后向平滑與抗差估計融合的SRCKF濾波[J].測繪通報，2017(4)：17-20.

10.13474/j.cnki.11-2246.2017.0111.

2016-07-22；

2016-12-31

江蘇省自然科學青年基金(BK20150236)；江蘇師范大學研究生科研創新計劃重點項目(2016YZD021)

孫 鵬(1991—)，男，碩士生，研究方向為GNSS數據處理。E-mail：spcxs@sohu.com

P207

A

0494-0911(2017)04-0017-04