不同焦距的連續像對相對定向嚴密公式

李忠美，邊少鋒，紀 兵

(海軍工程大學導航工程系，湖北 武漢 430033)

不同焦距的連續像對相對定向嚴密公式

李忠美，邊少鋒，紀 兵

(海軍工程大學導航工程系，湖北 武漢 430033)

針對現有解算相對定向元素的公式通常用于具有相同焦距的立體像對這一現狀，為充分利用不同相機所拍攝的現有影像信息，以像點坐標作為觀測量，給其加入改正數，借助計算機代數系統對共面方程進行嚴格的線性化，推導出了適用于解算不同焦距立體像對相對定向元素的嚴密公式；最后，通過算例驗證了該方法的正確性，可在一定程度上豐富攝影測量理論。

攝影測量；立體像對；相對定向；共面方程；線性化

立體像對的相對定向就是要恢復攝影時相鄰兩影像攝影光束的相互關系，一種是單獨像對相對定向，它采用兩幅影像的角元素運動實現相對定向；另一種是連續像對相對定向，它以左影像為基準，采用右影像的直線運動和角運動實現相對定向[1-4]。多個連續模型的處理中通常采用連續法相對定向。在傳統的連續像對相對定向中，多考慮理想的情況，將角元素視為小角，因此大大簡化了共面方程的線性化結果，得到近似的相對定向平差模型[5]。但是當連續像對相對定向法用于航偏角大的長航帶時，有可能會使后續像對的相對定向κ角偏大，以至于傳統的公式不能再使用。此時應該考慮更嚴密的解法，將像點坐標視為觀測量，如文獻[6—7]便將像點坐標而非上下視差作為觀測量，給其加入改正數，對共面方程進行嚴格的線性化，這種更嚴密的相對定向解法可適用于偏航角大的長航帶。然而，現有文獻中關于相對定向的研究多是針對同一航帶中的相同相機所拍攝的立體像對，即兩張像片具有相同的焦距[8-10]。實際上，隨著攝影測量影像獲取方式的多樣化[11-12]，覆蓋同一地區的影像并非僅來源于同一相機，此時需研究不同焦距情況下的相對定向方法,如文獻[13]將右片焦距作為待求參數，將相對定向元素個數增加至6個，然后通過將共面方程線性化，推導出了一種適用于可變焦距的相對定向公式，該公式適用于僅知一張像片焦距的情況。受以上文獻啟發，為充分利用不同相機所拍攝的現有影像信息，豐富攝影測量理論，本文將在現有文獻的基礎上，推導出適用于解算不同焦距的連續像對相對定向元素的公式。

1 共面方程及其線性化

1.1 共面方程表示

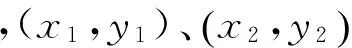
(1)

式中

(2)

另外，由于旋轉矩陣通常表示為φ、ω、κ轉角系

統，如下

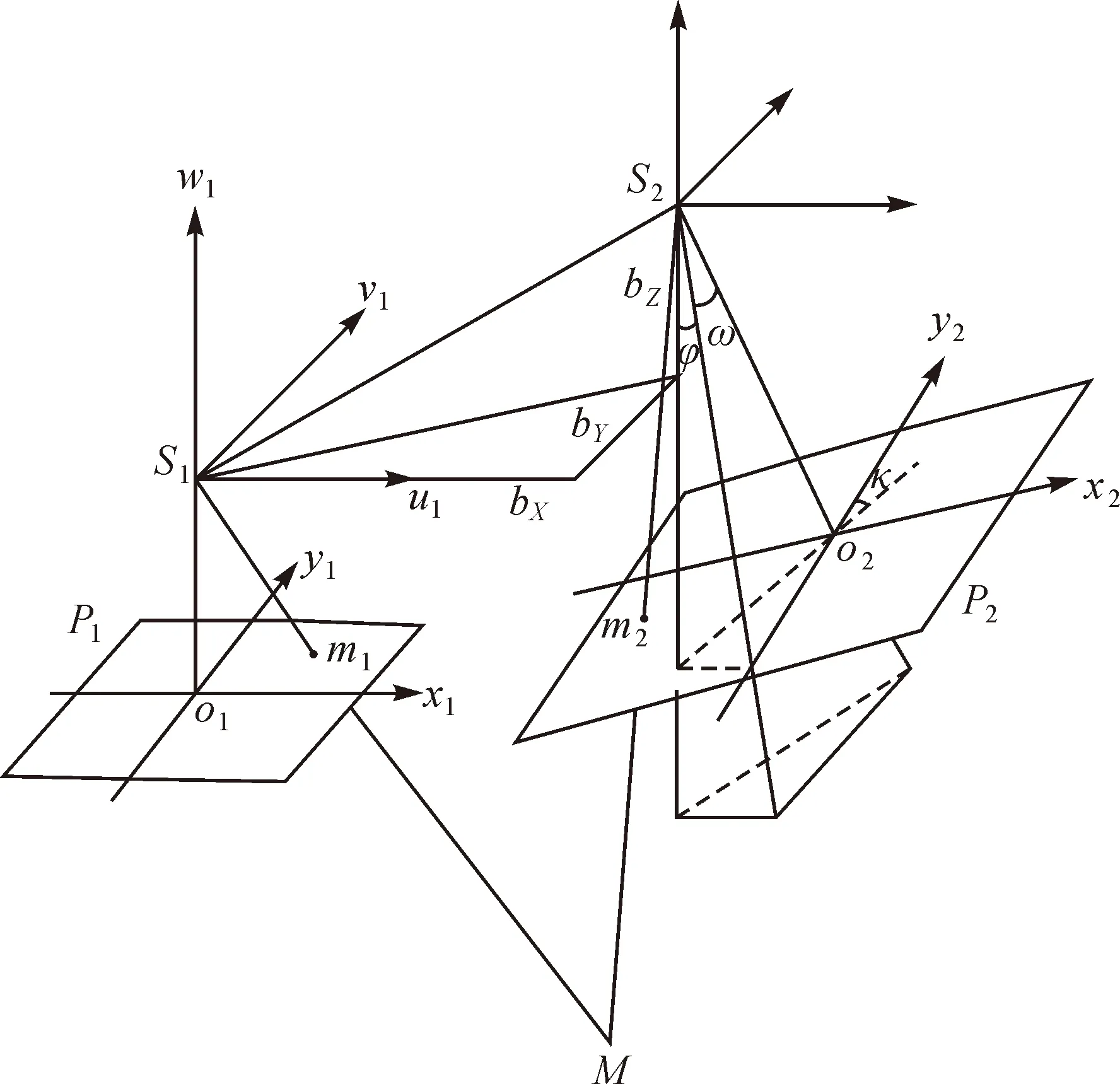
圖1 相對定向示意圖

(3)

將式(2)、式(3)代入式(1)中，可知共面方程中包含6個未知變量bX、bY、bZ、φ、ω、κ。由于bX僅影響相對定向模型大小，而不影響模型的建立，故可得相對定向元素為5個待求參數bY、bZ、φ、ω、κ。

1.2 共面方程線性化

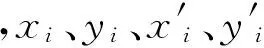
AiV+BiX+F0i=0

(4)

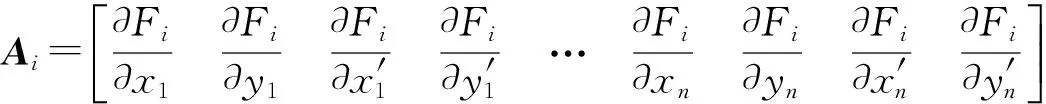
可借助計算機代數系統，推導出系數矩陣Ai、Bi中的各元素如下

2 最小二乘平差

2.1 計算過程

每對同名點可列1個形如式(4)的方程，由于相對定向元素為5個，當有5對觀測點時即可列出5個方程，求出5個待求參數。為了保證精度，通常進行多余觀測，然后借助最小二乘平差對其進行解算。由于像點坐標與相對定向元素同時作為模型中的未知量參與平差，故可根據附有參數的條件平差法[14-15]解算相對定向元素。主要步驟為：

(1) 記觀測權矩陣為P，為求出滿足VTPV=min的一組解，按求函數條件極值的方法，組成函數

(5)

式中，K是條件數。為求Φ的極小值，將其分別對V和X求一階導數，并令其等于零，可得

(6)

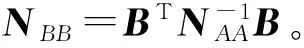
(3) 將相對定向元素改正數與限差相比，若小于限差，則改正數與初始近似值之和即為相對定向元素的值。否則，重復步驟(2)、(3)。反復趨近，直至改正數小于限差。

2.2 精度評定

由于每對同名點可列1個形如式(4)的方程，而待求參數個數為5個，則必須觀測5對同名點可唯一確定待求參數。因此可根據文獻[15]，得單位權中誤差的估值

(7)

則所求相對定向元素的精度為

(8)

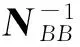
3 算例分析

為驗證本文算法的正確性及可靠性，以下通過兩組算例對其進行驗證。其中，算例1和算例2采用的數據分別為不含與包含觀測噪聲的像對。數據如下：已知左、右像片(A為小航偏角像對、B為中航偏角像對、C為大航偏角像對)的外方位元素真值見表1，在某區域范圍內選取9個地面點見表2，利用共線方程，可分別計算它們在左、右像片上對應的像點坐標(認為各像點坐標為等精度觀測)。

3.1 算例1(不含觀測噪聲像對的相對定向)

分別根據9對像點坐標，令BX=200 m，可利用本文連續像對相對定向公式解算小航偏角、中航偏角、大航偏角像對的相對定向元素，并將結果列于表3。

由表3可以看出，在像點坐標不含有觀測誤差時，利用本文方法分別對不同焦距的小航偏角、中航偏角、大航偏角像對進行連續相對定向，解算結果與真值相比，差異可忽略不計。此外，由于文中將像點坐標作為觀測量，且對相對定向元素的求導過程中不存在小角近似簡化。因此，該方法理論嚴密，且可用于解算大航偏角像對的相對定向元素。

表1 像對的外方位元素值

表2 地面點坐標值 m

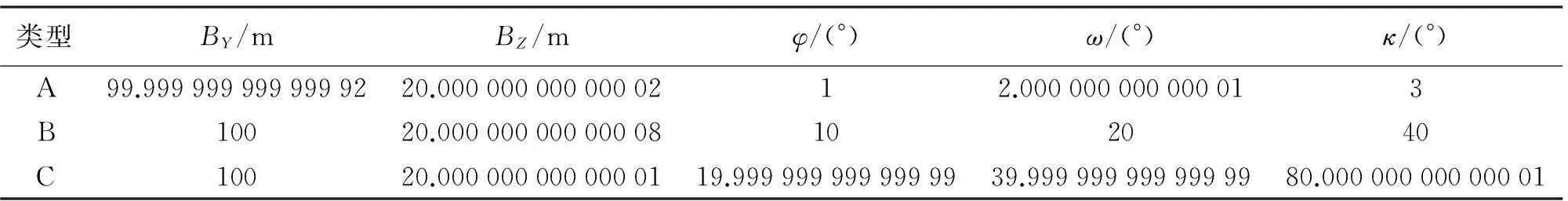
表3 不含觀測噪聲連續像對的相對定向結果

3.2 算例2(含有觀測噪聲像對的相對定向)

分別為9對像點坐標上加上0.5像素的量測誤差(像元大小為6 μm)，然后令BX=200 m，利用本文相對定向方法解算小航偏角、中航偏角、大航偏角像對的相對定向元素，并將結果列于表4。

表4 包含觀測噪聲連續像對的相對定向結果

由表4可以看出，在像點坐標含有0.5像素誤差時，利用本文方法進行連續像對相對定向元素解算時，與真值相比，小航偏角、中航偏角、大航偏角像對的相對定向角元素均可達到秒級精度，而小航偏角像對的相對定向線元素可達到毫米級精度，中航偏角、大航偏角像對的相對定向線元素具有厘米級精度。

綜上，本節利用兩組試驗數據(不含與包含觀測誤差的像點坐標)，分別對不同焦距的小、中、大航偏角像對進行相對定向元素解算，結果表明本文方法正確可靠且可適用于大航偏角像對。

4 結 語

本文以像點坐標作為觀測量，給其加入改正數，對共面方程進行線性化，推導了適用于不同焦距的連續像對相對定向元素解算公式，可得出結論如下：

(1) 該公式是對共面方程進行線性化而得，將像點坐標與相對定向元素同時作為模型中的未知量參與平差，其函數模型為附有參數的條件平差法。

(2) 當存在多于5對的同名像點時，可通過解算觀測量及待求參數的改正數后，反復迭代，趨近最終解。該方法在相對定向元素的求導過程中，不存在小角近似簡化，理論嚴密。

(3) 該公式可適用于解算不同焦距像對的相對定向元素，可處理不同相機拍攝的像片，提高現有影像信息的利用率，在一定程度上豐富了攝影測量理論。

[1] 張祖勛, 張劍清. 數字攝影測量學[M]. 武漢: 武漢大學出版社, 2014.

[2] 李德仁. 解析攝影測量學[M]. 北京: 測繪出版社, 1992.

[3] 張永軍, 胡丙華, 張劍清. 基于多種同名特征的相對定向方法研究[J]. 測繪學報, 2011, 40(2): 194-199.

[4] 王琳, 張力, 艾海濱. 無人飛行器遙感影像的自動相對定向研究[J]. 測繪通報, 2011(11): 11-14.

[5] 王佩軍, 徐亞明. 攝影測量學[M]. 武漢: 武漢大學出版社, 2013.

[6] MANSOUR F. Aerotriangulation by Coplanarity[J]. Journal of Engineering, 2006, 12(2): 247-258.

[7] 張劍清, 潘勵, 王樹根. 攝影測量學[M]. 武漢: 武漢大學出版社, 2014.

[8] 何海清, 程朋根, 王晉. 低空立體像對的嚴密相對定向[J]. 遙感信息, 2014, 29(6): 11-15.

[9] 張征宇, 朱龍, 黃敘輝, 等. 基于前方交會的5點相對定向[J]. 光學學報, 2015, 35(1): 231-238.

[10] 陸鈺, 陳義, 鄭波. 多基線近景攝影測量連續像對相對定向[J]. 同濟大學學報(自然科學版), 2010, 38(3): 442-447.

[11] 趙軍民, 魏新紅, 張凱. 一種改進的相對定向標定方法研究[J]. 科學工程與技術, 2013, 13(32): 9744-9748.

[12] 唐健林, 龍盈, 董文浩, 等. 航空攝影測量面陣相機與線陣相機數據生產工藝的研究[J]. 測繪通報, 2015(S0): 48-51.

[13] 田雷, 馬然. 無人機非量測相機檢校方法研究[J]. 測繪通報, 2016(7): 81-83.

[14] 王新洲, 陶本藻. 高等測量平差[M]. 北京: 測繪出版社, 2006.

[15] 武漢大學測繪學院測量平差學科組. 誤差理論與測量平差基礎[M]. 武漢: 武漢大學出版社, 2015.

Strict Solution to Relative Orientation of Successive Photo Pair with Different Focal Lengths

LI Zhongmei,BIAN Shaofeng,JI Bing

(Department of Navigation, Naval University of Engineering, Wuhan 430033, China)

Aiming at the status that mostly available methods for relative orientation are used for stereo images with the same focal length, in order to make full use of image information photographed by different cameras, with image point coordinates under correction, coplanarity equation is strictly linearized by computer algebra system, and strict solution for relative orientation of image pair with different focal lengths is carried out. Finally, the correctness of the formulae is verified by numerical examples. This method could enrich theories of photogrammetry to some degree.

photogrammetry; stereo images; relative orientation; coplanarity equation; linearization

李忠美，邊少鋒，紀兵.不同焦距的連續像對相對定向嚴密公式[J].測繪通報，2017(4)：35-38.

10.13474/j.cnki.11-2246.2017.0115.

2016-09-20；

2017-01-17

國家自然科學基金(41631072；41604010；41471387)

李忠美(1990—)，女，博士生，主要研究方向為攝影測量理論算法。E-mail：15827116839@163.com

P23

A

0494-0911(2017)04-0035-04