基于改進(jìn)集的向量均衡問題解的最優(yōu)性條件

宋寧寧， 仇秋生

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

基于改進(jìn)集的向量均衡問題解的最優(yōu)性條件

宋寧寧， 仇秋生

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

研究了帶約束向量均衡問題統(tǒng)一解的最優(yōu)性條件.首先,利用改進(jìn)集引進(jìn)了帶約束向量均衡問題E- 弱有效解和E- 有效解的概念;其次,在目標(biāo)函數(shù)為廣義凸的條件下,利用凸集分離定理和擇一定理獲得了向量均衡問題E- 弱有效解和E- 有效解的最優(yōu)性條件;最后,給出了向量?jī)?yōu)化問題相應(yīng)解的最優(yōu)性條件.

向量均衡問題;改進(jìn)集;E- 弱有效解;E- 有效解;最優(yōu)性條件

0 引 言

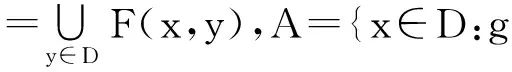
(VEP)

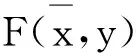
向量均衡問題是當(dāng)今運(yùn)籌學(xué)與非線性分析研究領(lǐng)域中的一個(gè)熱點(diǎn)問題,向量變分不等式、向量?jī)?yōu)化等均為向量均衡問題的特例.在數(shù)學(xué)規(guī)劃、工程技術(shù)、數(shù)理經(jīng)濟(jì)與社會(huì)經(jīng)濟(jì)系統(tǒng)等眾多領(lǐng)域中有著廣泛的應(yīng)用.而向量均衡問題包含各種不同形式的解,如:有效解、弱有效解、近似弱有效解、近似Henig有效解等.其中一個(gè)重要的問題是研究向量均衡問題的最優(yōu)性條件和標(biāo)量化特征.例如:2008年，龔循華[1]在局部凸空間中獲得了帶約束錐凸向量均衡問題的最優(yōu)性條件;2009年,仇秋生[2- 3]獲得了帶約束向量均衡問題的弱有效解和全局有效解的充分必要條件，以及弱有效解的K- T條件；2010年,龔循華等[4]獲得了Banach空間中無約束向量均衡問題近似解的最優(yōu)性條件；2011,龍憲軍等[5]運(yùn)用凸集分離定理，得到了近似錐次類凸向量均衡問題的Henig有效解及超有效解的充分必要條件,并運(yùn)用這些結(jié)果獲得了約束向量?jī)?yōu)化問題和向量變分不等式的最優(yōu)性條件;2012年,鮑玲玲等[6]在Banach空間中首先給出了帶約束向量均衡問題近似解的一些性質(zhì),并得到了帶約束向量均衡問題近似解的充分必要條件.近年來,一些學(xué)者[7- 9]利用改進(jìn)集對(duì)向量?jī)?yōu)化問題解的統(tǒng)一性進(jìn)行了研究,但對(duì)向量均衡問題解的統(tǒng)一性研究暫時(shí)還沒有相關(guān)結(jié)果.如何提出統(tǒng)一的向量均衡問題解的概念并在統(tǒng)一的框架下研究它們的最優(yōu)性條件、標(biāo)量化、存在性等工作具有重要的實(shí)際和理論意義.

本文研究了改進(jìn)集下帶約束向量均衡問題統(tǒng)一解的最優(yōu)性條件.首先,在文獻(xiàn)[1- 2,7,10- 11]的基礎(chǔ)上,利用改進(jìn)集引進(jìn)了帶約束向量均衡問題E- 弱有效解和E- 有效解的相關(guān)概念,并討論了它們之間的關(guān)系;其次,給出了內(nèi)部E- 類凸映射的擇一定理;最后,獲得了廣義次類凸向量均衡問題的E- 弱有效解的充分與必要條件,并利用擇一定理獲得了向量均衡問題的E- 有效解的充分條件.

1 相關(guān)概念與引理

設(shè)C?Y是點(diǎn)凸錐,C的共軛錐和C的擬內(nèi)部分別用C*和C#表示,即

C*:={y*∈Y*:y*(y)≥0,?y∈C};

C#:={y*∈Y*:y*(y)>0,?y∈C{0}}.

由C誘導(dǎo)出Y的偏序，即?y∈Y,有

x≤Cy??y-x∈C.

設(shè)S為Y的任意一個(gè)非空子集,S的生成錐記為:cone(S):={λs:λ≥0,s∈S}.記cone+(S):={λs:λ>0,s∈S},顯然

1)cone(S)=cone+(S)∪{0Y};

2)cl(cone(S))=cl(cone+(S));

3)cone+(S+C)=cone+(S)+C.

引理1[10]設(shè)M是Y中的凸集,則cl(M)是凸的.此外,若intM≠?,則intM是凸的且cl(M)=cl(intM),intM=int(cl(M)).

引理2[10]設(shè)S是Y中的任意子集,C是內(nèi)部非空凸錐,則

1)cl(S+C)=cl(S+intC);

2)int(cl(S+C))=S+intC;

3)int(S+C)=S+intC.

定義1[7]設(shè)E是Y中的非空子集.若0?E且E+C=E,則稱E為改進(jìn)集.記LY是Y中所有改進(jìn)集組成的集合.

引理3[7]設(shè)E∈LY,C是Y中的閉凸點(diǎn)錐,且intC≠?,則

1)intE=E+intC;

2)cl(cone(D+E))=cl(cone(D+intE)).

注1 由引理3表明:當(dāng)intC≠?時(shí),intE≠?.

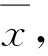
(VEPC)

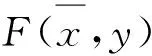
其中,E∈LY.

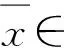
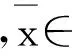
下面給出基于改進(jìn)集的向量均衡問題相關(guān)解的定義.

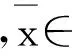
注2 設(shè)intE≠?,顯然E- 有效解一定是E- 弱有效解.

注3 基于改進(jìn)集的帶約束向量均衡問題的解是一個(gè)很一般的概念,它統(tǒng)一了已知的很多帶約束向量均衡問題解的概念.例如:

1)記E=ε+C{0},ε≥0,于是E∈LY.當(dāng)ε=0時(shí),(VEPC)的E- 有效解就是(VEP)的有效解;當(dāng)ε≠0時(shí),(VEPC)的E- 有效解就是(VEP)的ε- 有效解.

2)記E=ε+intC,ε≥0,顯然E∈LY.當(dāng)ε=0時(shí),(VEPC)的E- 弱有效解就是(VEP)的弱有效解;當(dāng)ε≠0時(shí),(VEPC)的E- 弱有效解就是(VEP)的ε- 弱有效解.

3)當(dāng)intC?E?C{0}且C是Y中的點(diǎn)凸錐時(shí),(VEPC)的E- 弱有效解為(VEP)的弱有效解.

定義4 設(shè)F:D→Y,E∈LY.若int(cone+(F(D)+E))是凸集,且cone+(F(D)+E)?cl(int(cone+(F(D)+E))),則稱F為D上內(nèi)部E- 類凸的.

其等價(jià)定義:F是D上內(nèi)部E- 類凸的當(dāng)且僅當(dāng)int(cone+(F(D)+E))是凸集,且F(D)+E?cl(int(cone+(F(D)+E))).

注4 顯然,F是D上內(nèi)部E- 類凸的當(dāng)且僅當(dāng)int(cone+(F(D)+E))是凸集,且

cl(cone+(F(D)+E))=cl(int(cone+(F(D)+E))).

定義5[7]設(shè)F:D→Y.若cl(cone(F(D)+E))是凸集,則稱F為D上近似E- 次類凸的.

注5 由引理3及文獻(xiàn)[11]中的命題3.3知,當(dāng)intC?E?C{0}且C是Y中的閉凸點(diǎn)錐時(shí),cl(cone(F(D)+E))=cl(cone(F(D)+C)).這表明在此條件下,近似C- 次類凸映射和近似E- 次類凸一致.反之,近似C- 次類凸映射不一定是近似E- 次類凸的.

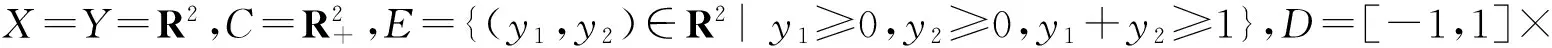
顯然,cl(cone(f(D)+E))是凸集,而cl(cone(f(D)+E))不是凸集.

命題1 若int(cone+(F(D)+E))≠?,則下列命題等價(jià):

1)cl(cone+(F(D)+E))是凸集且int(cl(cone+(F(D)+E)))=int(cone+(F(D)+E));

2)F是D上內(nèi)部E- 類凸的.

證明 1)?2) 由于cl(cone+(F(D)+E))是凸集且

int(cl(cone+(F(D)+E)))=int(cone+(F(D)+E))≠?,

所以由引理1得int(cl(cone+(F(D)+E)))是凸集,且

cl(cone+(F(D)+E))=cl(int(cone+(F(D)+E))).

又由int(cl(cone+(F(D)+E)))=int(cone+(F(D)+E))知,int(cone+(F(D)+E))是凸集且

F(D)+E?cl(cone+(F(D)+E))=cl(int(cone+(F(D)+E))).

即2)成立.

2)?1) 假設(shè)F是D上內(nèi)部E- 類凸的,則由定義4知int(cone+(F(D)+E))是凸集,從而cl(int(cone+(F(D)+E)))是凸集.又由注4知,cl(int(cone+(F(D)+E)))=cl(cone+(F(D)+E)),于是cl(cone+(F(D)+E))是凸集.因?yàn)閕nt(cone+(F(D)+E))≠?,所以由引理1知,

int(cl(cone+(F(D)+E)))=int(cone+(F(D)+E)).

即1)成立.命題1證畢.

注6 1)當(dāng)intC≠?時(shí),由引理2易證int(cl(cone+(F(D)+E)))=int(cone+(F(D)+E)).由命題1可知在此條件下內(nèi)部E- 類凸與近似E- 次類凸是一致的.

2)由命題1知:若F在D上是內(nèi)部E- 類凸的,則F在D上是近似E- 次類凸的,反之不一定成立.

例2 設(shè)X=Y=R2,C={(0,t)∈R2:t≥0},D=C,E=C{0Y}.令f:D→Y,f(x)=x,?x∈D.顯然,cl(cone+(f(D)+E))=C是凸集,但int(cone+(f(D)+E))=?.于是,f在D上不是內(nèi)部E- 類凸的.

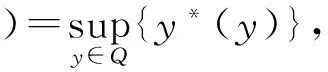
定理1 設(shè)F:D→Y為D上內(nèi)部E- 類凸的映射,則下面2個(gè)結(jié)論有且只有1個(gè)成立:

1)0∈int(cone+(F(D)+E)) ;

2)?y*∈C*{0},使得〈y*,F(x)〉≥σ-E(y*),?x∈D.

證明 若1)不成立,則2)成立.設(shè)0?int(cone+(F(D)+E)),則由凸集分離定理可知:存在y*∈Y*{0},使得

〈y*,y〉>0, ?y∈int(cone+(F(D)+E)).

由式(1)可得,〈y*,y〉≥0,?y∈cl(int(cone+(F(D)+E))).因?yàn)镕是D上內(nèi)部E- 類凸的,所以

〈y*,y〉≥0, ?

即〈y*,F(x)+e〉≥0,?x∈D,?e∈E.因此,〈y*,F(x)〉≥σ-E(y*),?x∈D.

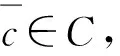
〈y*

由E∈LY和式(2)可得

〈y*,y′〉≥0, ?

若1)成立,則2)不成立.由于1)成立,所以存在零鄰域UY,使得UY?cone+(F(D)+E).若2)也成立,則〈y*,F(x)+e〉≥0,?x∈D,?e∈E,即〈y*,y′〉≥0,?y′∈cone+(F(D)+E).

由于UY?cone+(F(D)+E),所以〈y*,y′〉≥0,?y′∈UY.于是,y*=0.與y*≠0矛盾.定理1證畢.

2 最優(yōu)性條件

下面利用凸集分離定理給出近似(E×K)- 次類凸向量均衡問題的弱有效解的充分必要條件.

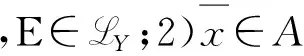
(φ).

(h(D)+E×K)∩((-intC)×(-intK))=?.

若式(6)不成立,則存在y∈D,e∈E,k∈K,c∈intC,k0∈intK ,使得

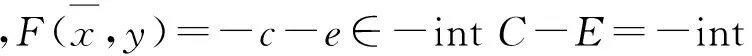
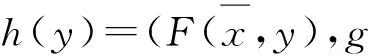
〈(φ,ψ),cl(cone(h(D)+E×K))〉>〈φ,-intC〉+〈ψ,-intK〉.

由cl(cone(h(D)+E×K))是凸錐及式(9)可得,〈(φ,ψ),cl(cone(h(D)+E×K))〉≥0.顯然,

〈(φ,ψ),h(D)+E×K〉≥0.

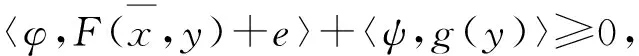
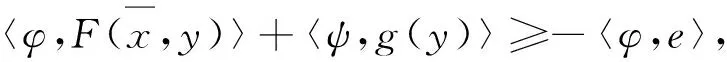
?e∈E, ?

由式(10)得

(φ).

于是,式(5)成立.

另一方面,由(0Y,0Z)∈cl(cone(h(D)+E×K))和式(9)可得〈φ,-intC〉+〈ψ,-intK〉<0.顯然,對(duì)?c∈intC,?λ>0,有λc∈intC,則

〈φ,-λc〉<〈ψ,k〉, ?c∈intC, ?λ>0, ?k∈intK.

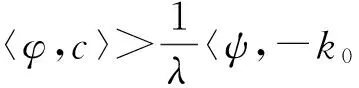
〈φ,c〉≥0, ?

又因?yàn)镃是凸的且intC≠?,所以C?cl(C)?cl(intC).因此,由式(11)可知φ∈C*.同理可證ψ∈K*.

下證φ≠0Y*.否則,由(φ,ψ)≠(0Y*,0Z*)和式(10)可知

〈ψ,g(y)〉≥0, ?

又由于ψ∈K*,g(x0)∈-intK,所以〈ψ,g(x0)〉<0.與式(12)矛盾.因此,φ∈C*{0}.

C.

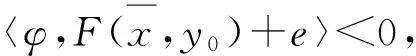
(φ).

注7 定理2獲得了向量均衡問題的E- 弱有效解的充要條件,而E- 弱有效解包含許多已知的解作為特殊情況,如:

1)令E=ε+intC,ε≥0.當(dāng)ε=0時(shí),(VEPC)的E- 弱有效解最優(yōu)性條件就是(VEP)的弱有效解的最優(yōu)性條件;當(dāng)ε≠0時(shí),(VEPC)的E- 弱有效解就是(VEP)的ε- 弱有效解.從而推廣了文獻(xiàn)[2]中定理3.1的結(jié)果.

2)當(dāng)intC?E?C{0}且C是Y中的點(diǎn)凸錐時(shí),(VEPC)的E- 弱有效解為(VEP)的弱有效解.

(φ).

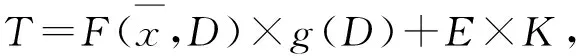
UY×UZ?cone+(T).

取d′∈C{0},使得-d′∈UY{0}.由式(13)知,(-d′,0)∈UY×UZ?cone+(T),即存在λ>0,y′∈D,e∈E,k∈K,使得

(y′)+k).

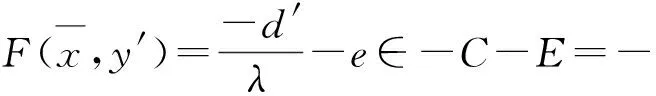
(ψ).

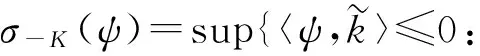
(φ).

下證φ≠0Y*.否則由式(16)可得〈ψ,g(y)〉≥0,?y∈D.因?yàn)閷?duì)任意的k∈K,有〈ψ,k〉≥0,所以〈ψ,g(y)+k〉≥0,?y∈D,?k∈K.顯然,

〈ψ,z)〉≥0, ?z∈cl(cone(g(D)+K)).

又因?yàn)閏l(cone(g(D)+K))=Z,所以

〈ψ,z)〉≥0, ?z∈Z.

而-z∈Z,故由式(17)可知,〈ψ,z〉≤0.因此,ψ為零泛函.這與(φ,ψ)∈(C*×K*){0Y*,0Y*}矛盾.故φ≠0Y*.定理3證畢.

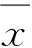
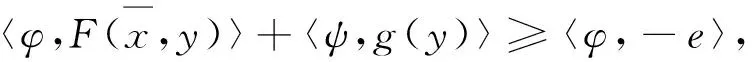
?e∈E, ?

由于ψ∈K*,所以〈ψ,g(y)〉≤0,?e∈E,?y∈A.因此,由式(19)可知

?e∈E, ?y∈A.

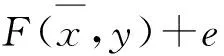
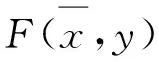
?-e-C?-(E+C)=-E, ?y∈A.

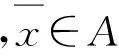
3 應(yīng) 用

下面以向量?jī)?yōu)化問題為例,給出改進(jìn)集下向量?jī)?yōu)化問題的相關(guān)結(jié)果.

設(shè)f:X→Y,g:Y→Z.所謂改進(jìn)集下向量?jī)?yōu)化問題(VOP)就是:找出x∈A,使得

(VOP)

f(y)-f(x)?-E, ?y∈A.

當(dāng)取F(x,y)=f(y)-f(x),?x,y∈D時(shí),(VEPC)即轉(zhuǎn)化為(VOP).顯然,(VOP)為(VEPC)的一種特殊情形.

〉.

).

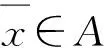
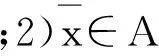
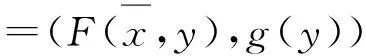
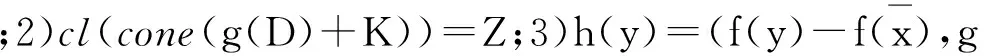
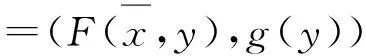
[1]Gong Xunhua.Optimality conditions for vector equilibrium problems[J].J Math Appl,2008,46(1):155- 161.

[2]Qiu Qiusheng.Optimality conditions for vector equilibrium problems with constraints[J].J Ind Manag Optim,2009,5(4):783- 790.

[3]Qiu Qiusheng.Optimality conditions of globally efficient solution for vector equilibrium problems with generalized convexity[J].J Inequal Appl,2009,2009(1):1- 13.

[4]龔循華,熊淑群.Banach空間中向量均衡問題的近似解的最優(yōu)性條件[J].南昌大學(xué)學(xué)報(bào):理科版,2010,34(2):103- 107.

[5]Long X J,Huang Y Q,Peng Z Y.Optimality conditions for the Henig efficient solution of vector equilibrium problems with constraints[J].Optim Lett,2011,5(4):717- 728.

[6]鮑玲玲,仇秋生.Banach空間中向量均衡問題的近似解的最優(yōu)性條件[J].浙江師范大學(xué)學(xué)報(bào):自然科學(xué)版,2012,35(1):18- 23.

[7]Zhao Kequan,Yang Xinmin,Peng Jianwen.WeakE- optimal solution in vector optimization[J].Taiwan J Math,2013,17(4):1287- 1302.

[8]Chicco M,Mignanego F,Pusillo L,et al.Vecter optimization problems via improvement sets[J].J Optim Theory Appl,2011,150(3):516- 529.

[9]Oppezzi P,Rossi A.Improvement sets and covergence of optimal points[J].J Optim Theory Appl,2015,165(2):405- 419.

[10]Sach P H.New generalized convexity notion for set- valued maps and application to vector optimization[J].J Optim Throry Appl,2005,125(1):157- 179.

[11]Yang X M,Li D,Wang S Y.Near- subconvexlikeness in vector optimization with set- valued fuctions[J].J Optim Throry Appl,2001,110(2):413- 427.

(責(zé)任編輯 陶立方)

The optimality conditions of the vector equilibrium problems via improvement set

SONG Ningning, QIU Qiusheng

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

The optimality conditions for unified solution of the vector equilibrium problems with constraints were studied. Firstly, the concept ofE- weakly efficient solution andE- efficient solution for the vector equilibrium problems with constraints via the improvement set were introduced. Secondly, under the condition of generalized convex function, the optimality conditions forE- weakly efficient solution andE- efficient solution of the vector equilibrium problems were given. Finally, the optimality conditions of vector optimization problems were obtained.

vector equilibrium problems; improvement set;E- weakly efficient solution;E- efficient solution; optimality conditions

10.16218/j.issn.1001- 5051.2017.02.003

2016- 04- 25；

2016- 06- 19

國(guó)家自然科學(xué)基金資助項(xiàng)目(11471291)

宋寧寧(1989-),女，河南周口人，碩士研究生.研究方向：最優(yōu)化理論.

仇秋生. E- mail： qisqiu@zjnu.cn

O221.6

A

1001- 5051(2017)02- 0130- 07