煙氣流速對湍流渦旋以及顆粒凝并影響的研究

陳亞偉， 熊揚恒， 潘祖明， 周建龍， 周 盟

(1.武漢大學 動力與機械學院，武漢 430072； 2.武漢利康能源有限公司，武漢 430000)

煙氣流速對湍流渦旋以及顆粒凝并影響的研究

陳亞偉1， 熊揚恒1， 潘祖明2， 周建龍1， 周 盟1

(1.武漢大學 動力與機械學院，武漢 430072； 2.武漢利康能源有限公司，武漢 430000)

采用歐拉-拉格朗日法結合O'Rouekr碰撞模型，模擬了電廠滿負荷下靜電除塵器前的煙道流速區間內顆粒物的碰撞和凝并.結果表明：凝并器入口煙氣流速越大，凝并區的湍流強度和渦量越大，有利于減少細顆粒物的數量，但減少的幅度較小；凝并器入口煙氣流速越大，顆粒物在凝并區的停留時間越短，碰撞凝并形成的顆粒物粒徑也越小，不利于形成粒徑較大的顆粒物，所研究的電廠常見煙氣流速范圍內凝并器入口煙氣流速的提高對湍流凝并的負面作用大于正面作用.

細顆粒物； 煙氣流速； 顆粒停留時間； 湍流凝并

近年來，可吸入顆粒物(PM10)特別是空氣動力學直徑小于2.5 μm的細顆粒物(PM2.5)已取代SO2和NOx成為我國首要的大氣污染物.細顆粒物能夠長期懸浮于大氣環境中，具有較大的比表面積，可以吸附大量的重金屬等有害物質，一旦進入人體沉積，將會對呼吸系統產生嚴重危害.

目前，靜電除塵器以除塵效率高、能耗低、處理煙氣量大、能處理高溫氣體和技術比較成熟等優點被廣泛應用于除塵行業[1].靜電除塵器的除塵效率可以達到99.9%以上，但是由于細顆粒物的荷電能力弱，因此仍有一大部分的細顆粒物被排放到空氣中，使燃煤電站無法達到最新的排放標準.湍流凝并作為一種煙氣預處理技術，因其改造簡單及運行和維護成本低，成為近年來國內外的一個研究熱點.湍流凝并是指在靜電除塵器前的煙道安裝擾流裝置，通過產渦和增加氣流擾動，增大顆粒物的碰撞概率，從而使細顆粒物凝并成粒徑較大的顆粒物，進而被靜電除塵器捕獲.

電廠在滿負荷運行的情況下，靜電除塵器前的煙道內煙氣流速約為10～14 m/s，煙氣流速不僅會影響到顆粒物的運動和碰撞，還會影響流場的湍流強度和渦量大小.樊建人等[2]的研究表明，流速越大、控制體內顆粒物數量越多，顆粒物的碰撞概率越大.劉忠等[3]對凝并器內的流場和顆粒物運動軌跡進行了模擬，結果表明，流速越大，顆粒物受湍流的影響越大，發生碰撞凝并的概率也越大.韓光[1]對7 m/s、10 m/s和14 m/s 3種煙氣流速下產渦裝置的凝并效果進行了模擬，結果表明，流速越大，湍流強度越強，渦量越大，碰撞的概率也就越大，越有利于細顆粒物的凝并.但同時韓光等人也指出，上述結論只是單從氣流方面來說，具體效果還應該考慮流速對顆粒物運動的影響.煙氣流速對顆粒物運動的直接影響就是顆粒物在凝并器內的停留時間，停留時間的長短直接影響單位時間內所研究控制體內顆粒物的濃度，而顆粒物的濃度又會對顆粒物的凝并效果產生影響.

筆者運用商業計算流體力學(CFD)軟件Fluent模擬不同凝并器入口煙氣流速下單通道內顆粒物的流動及凝并，通過對顆粒物停留時間和凝并器出口處不同粒徑顆粒物數量百分數分布進行分析，研究煙氣流速對細顆粒物凝并的影響.

1 數學模型

1.1 流場與顆粒場計算模型

本文研究對象屬于氣固兩相流，由于顆粒物的體積率小于10%，因此采用歐拉-拉格朗日法進行模擬[4].對于連續相，流體作為連續介質在歐拉坐標系下進行描述.首先采用穩態計算得到迭代初場，然后采用分離渦模型(DDES)[5-6]進行非穩態計算.壓力-速度耦合采用Simple算法，壓力-連續方程采用Presto方法，k、ε均取二階迎風格式，動量采用有界中心差分格式，非穩態項采用有界二階隱式格式.對于離散相，采用離散項模型在拉格朗日坐標系下進行描述，顆粒物運動選用隨機游走模型，顆粒物碰撞及凝并采用O'Rouekr碰撞運算法則[7-8].

計算選用非穩態模型，時間步長設置為0.001 s，共計算1 000步.流場入口選用速度入口模型，每一個時間步長在凝并器入口均勻入射520個粒子，其中直徑為0.1 μm的粒子數量占25%，1 μm的占50%，10 μm的占25%.流場出口設置為自然出流，顆粒物為逃逸型.壁面采用無滑移標準壁面函數，壁面和凝并元件均采用彈性碰撞.

1.2 顆粒受力分析

顆粒物在流場中的運動狀態是其所受的多種力混合作用的結果.按照顆粒受力的來源可分為：顆粒物自身在場的作用下產生的力(體積力)、氣體對顆粒物的作用力(浮力、黏性阻力、虛擬質量力、壓力梯度力、Basset力、Magnus升力和Saffman升力)以及顆粒物之間的相互作用力[9].但是在實際計算時，由于顆粒物質量很小且在凝并器內的運動時間很短，可以忽略重力和浮力的影響.

(1) 黏性阻力.

黏性阻力是影響顆粒物運動的重要因素，只要顆粒物與氣體間存在相對運動，就會有黏性阻力的存在.對于勻速、等溫、不可壓縮黏性流體，假設顆粒物為球狀，則當單個顆粒物在流體中運動且具有相對速度(vf-vp)時，由于流體的黏性，顆粒物受到的流體黏性阻力FD可表示如下：

(1)

式中：dp為顆粒物直徑；ρf為連續相密度；CD為阻力系數；vf和vp分別為流體和顆粒物的速度.

黏性阻力系數CD是與顆粒物雷諾數有關的量，顆粒物雷諾數可由式(2)求出：

(2)

式中:μ為顆粒物的動力黏度.

(2) 虛擬質量力.

當顆粒物相對流體做加速運動時，不但顆粒物速度越來越大，而且顆粒物周圍流體的速度也會增大.推動顆粒物運動的力不但用于增加顆粒物本身的動能，同時也增大了顆粒物周圍流體的動能，因而該力將大于用于加速顆粒物的力，相當于顆粒物的質量增加，所以將這部分增加質量的力稱為虛擬質量力，其表達式如下：

(3)

對于氣固兩相流，由于氣體密度遠遠小于顆粒物的密度，所以虛擬質量力相對于慣性力而言可以忽略不計.

(3) 壓力梯度力.

在有壓力梯度的流動中，由于顆粒物周圍流體壓力梯度的存在，總有壓力的合力作用于顆粒物上，其表達式如下：

(4)

該力的大小等于顆粒物的體積與壓力梯度的乘積，方向與壓力梯度相反.在通常情況下，氣體的加速度與顆粒物的加速度處于同1個數量級，而氣體的密度則比顆粒物的密度小3個數量級，由此說明，壓力梯度力比顆粒物本身的慣性力小3個數量級，通常可以忽略不計[11].

(4)Basset力.

Basset力是指顆粒物在黏性流體中進行急劇加速運動時(或非穩態運動時)所受到的一種黏性阻力，其表達式如下：

(5)

式中：t0為開始時刻；t′為積分變量；μf為黏性流體的動力黏度.

研究表明，對于氣固兩相流，由于氣體密度遠小于顆粒物密度，因此Basset力通常可以忽略不計.

(5) Magnus升力.

若在流場中存在速度梯度，該速度梯度可以引起顆粒物的旋轉.此時，除球體因速度梯度發生旋轉外，還因速度大的一側壓力小，速度小的一側壓力大，產生的壓力差將推動球體向速度大的一側移動，這種推動力稱為Magnus升力.其表達式如下：

(6)

式中：ω為顆粒物旋轉角速度.

除近壁區外，在流場大部分區域顆粒物受到的Magnus升力不明顯，Magnus升力比黏性力至少要小1個數量級，可以忽略不計.

(6) Saffman升力.

Saffman證明，當顆粒物處在有速度梯度的流場中時，即使顆粒物沒有旋轉，其也受一橫向升力，該力稱為Saffman升力.Saffman升力與Magnus升力不同，它不是由于顆粒物旋轉產生的，而是由速度梯度引起的.Saffman升力Fs的表達式如下：

(7)

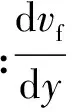
當剪切流動較大時，Saffman升力應予以考慮.

綜上所述，在研究顆粒物的運動和碰撞時，主要考慮顆粒物所受到的黏性阻力和Saffman升力，這樣既不會影響計算的準確性，又可以簡化模型，節約計算成本.

2 物理模型

計算區域為長1 800 mm、寬100 mm、高70 mm的長方體單通道，在凝并器通道兩側壁面布置9級對稱的凝并元件(擾流片)，第一級凝并元件距凝并器入口50 mm，每級間距180 mm.凝并元件結構[8]如圖1所示.

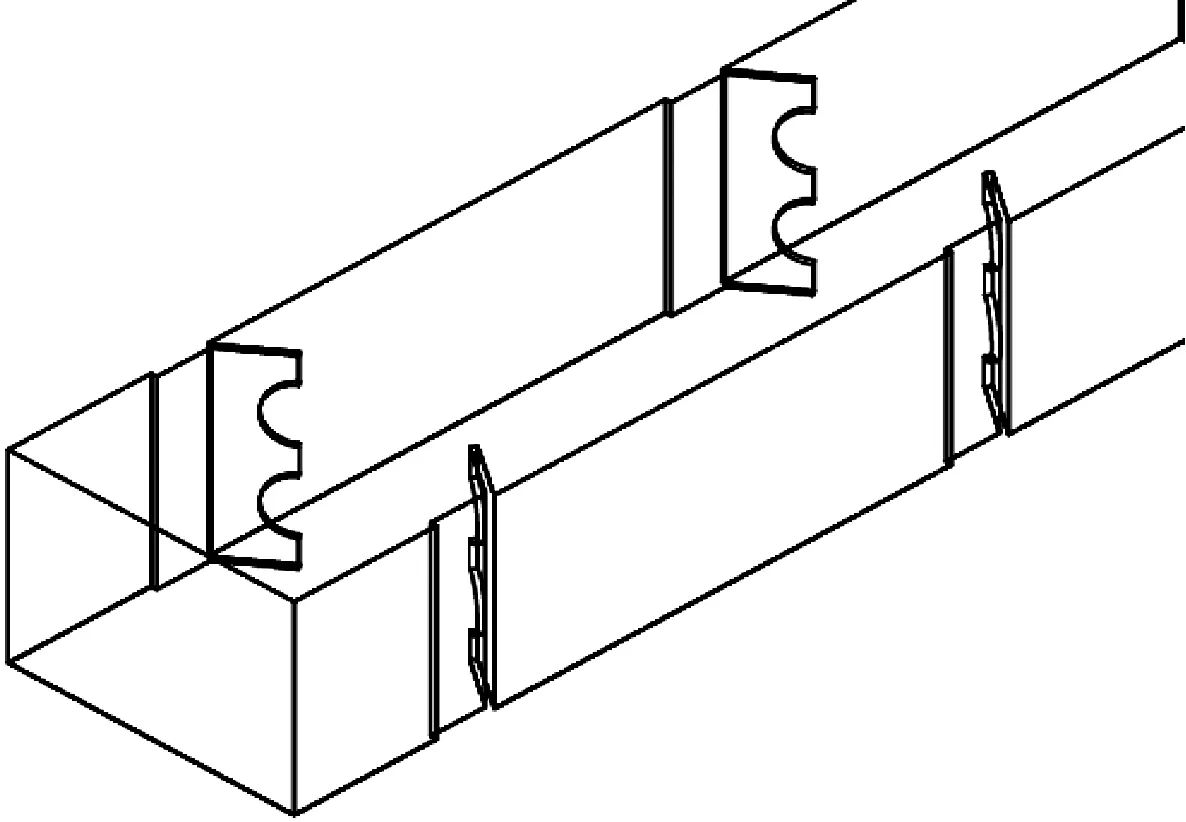
圖1 凝并元件結構示意圖

3 模擬結果與分析

電廠在滿負荷運行時，靜電除塵器前煙道內的煙氣流速約為10～14 m/s，因此選取10 m/s、12 m/s和14 m/s 3種情況作為研究對象，每個時間步長在凝并器入口處均勻入射520個粒子，其中直徑為0.1 μm的顆粒物占25%，1 μm的占50%，10 μm的占25%.在凝并器出口對顆粒物進行隨機采樣，分析凝并器出口顆粒物的停留時間和粒徑分布.

3.1 不同凝并器入口煙氣流速下流場的湍流強度和渦量

凝并器入口煙氣流速對流場的影響主要體現在流場的湍流強度(Turbulent Kinetic Energy-k)和渦量(Vorticity Magnitude)大小上，而流場的湍流強度和渦量又是影響顆粒物碰撞和凝并的2個重要因素.表1給出了3種典型凝并器入口流速下計算區域總的湍流強度和渦量以及平均湍流強度和渦量.

表1 不同凝并器入口煙氣流速下流場的湍流強度和渦量

Tab.1 Turbulent intensity and vorticity of flow field under different flue gas velocities at coagulator inlet

入口煙氣流速v/(m·s-1)總湍流強度/(m2·s-2)總渦量/s-1平均湍流強度/(m2·s-2)平均渦量/s-1101．55×1077．11×1094．56633．56122．06×1077．87×1097．00731．38142．67×1078．20×1098．40831．83

由表1可知，隨著凝并器入口煙氣流速的增大，流場的湍流強度和渦量也隨之增大，這與之前學者的研究結果相符[13].

3.2 不同凝并器入口煙氣流速下顆粒物的停留時間

顆粒物在凝并器內的運動時間是由凝并器入口煙氣流速、凝并器結構、流場條件以及顆粒物粒徑等多種因素共同決定的.其中，凝并器入口煙氣流速是影響顆粒物在凝并器內停留時間的重要因素.圖2和圖3分別為不同凝并器入口煙氣流速下顆粒物數量遞減百分數隨時間變化圖和顆粒物數量百分數分布圖.

圖2 不同凝并器入口煙氣流速下不同停留時間的顆粒物數量遞減百分數

Fig.2 Degressive percentage of the number of particles at different retention time under various flue gas velocities at coagulator inlet

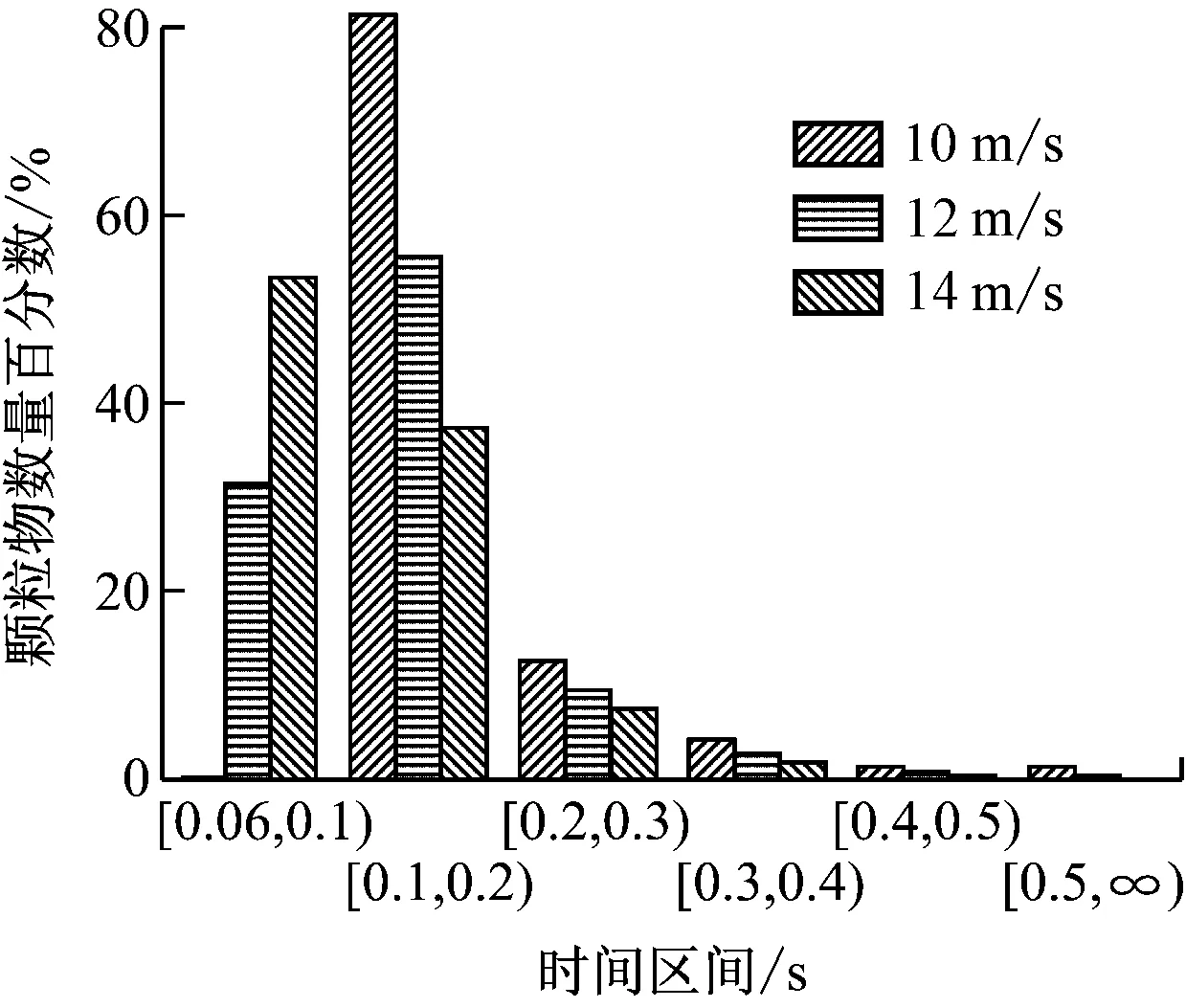
圖3 不同凝并器入口煙氣流速下不同停留時間區間的顆粒物數量百分數

Fig.3 Percentage of the number of particles in different intervals of retention time under varions flue gas velocities at coagulator inlet

從圖2可以看出，隨著凝并器入口煙氣流速的增大，顆粒物數量百分數隨時間的遞減曲線向橫軸的左側移動，停留時間長時顆粒物數量減少，停留時間短時顆粒物數量增加.同樣，從圖3也可以看出，當凝并器入口煙氣流速為10 m/s時，幾乎沒有顆粒物的停留時間在0.1 s以下；而當凝并器入口煙氣流速增大到12 m/s時，停留時間在0.1 s以下的顆粒物數量百分數就已經超過了30%；當凝并器入口煙氣流速達到14 m/s時，這一百分數更是超過了50%.凝并器入口煙氣流速越高，在凝并區停留時間長的顆粒物越少，大量顆粒物很快地運動出凝并區，降低了凝并區的顆粒物濃度，從而影響顆粒物的碰撞和凝并.

3.3 不同凝并器入口煙氣流速下顆粒物的凝并效果

從第3.1節和第3.2節的研究可以看出，一方面，凝并器入口煙氣流速的增大可以增大流場的湍流強度和產渦效果，有利于增加顆粒物的碰撞次數，提高凝并效果；另一方面，隨著流速的增大，顆粒物在凝并區的停留時間變短，造成凝并區的顆粒物濃度降低，凝并效果變差.因此，筆者重點研究凝并器入口煙氣流速和顆粒物在凝并區的停留時間對凝并效果的影響，并找出起主導作用的一方.圖4和圖5分別給出了凝并器出口不同粒徑顆粒物數量百分數遞減曲線以及不同粒徑區間的顆粒物數量百分數.

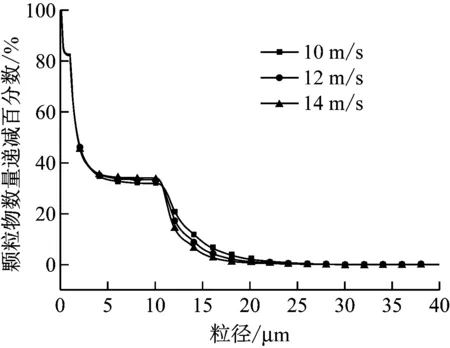
圖4 凝并器出口不同粒徑顆粒物數量遞減百分數

Fig.4 Degressive percentage of the number of particles with different diameters at coagulator outlet

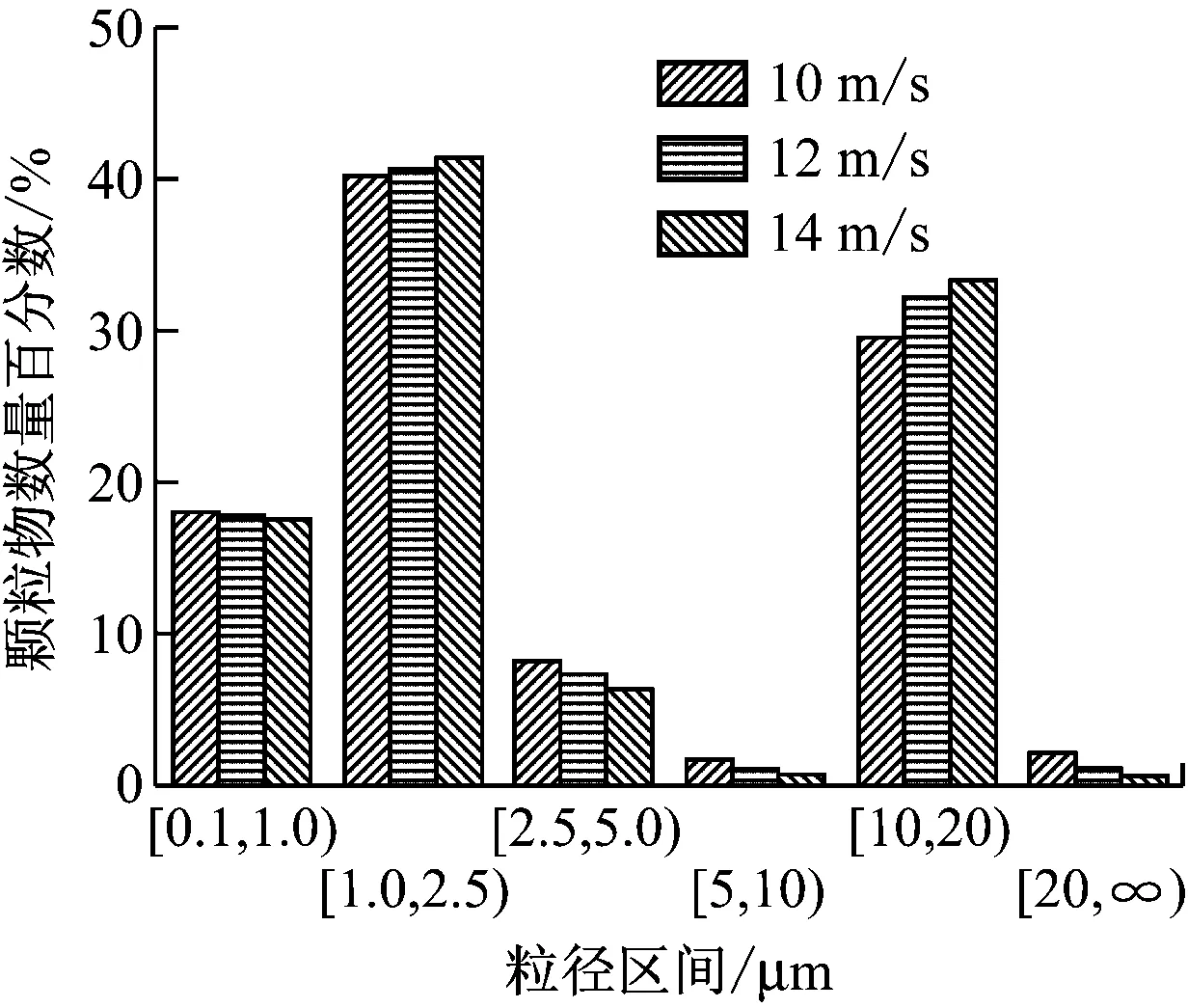
圖5 不同粒徑區間顆粒物數量百分數

模擬結果顯示，在0.1～<1 μm區間，煙氣流速高時顆粒物數量百分數較小；在1～<2.5 μm和10～<20 μm區間內煙氣流速越高，顆粒物數量百分數越大；而在2.5～<5 μm、5～<10 μm以及20 μm以上3個區間，顆粒物數量百分數隨煙氣流速的增大而減小.這是因為當煙氣流速較高時，由于流場的湍流強度大、產渦效果好，增大了細顆粒物之間以及細顆粒物與粒徑大的顆粒物之間的碰撞凝并概率，因此煙氣流速越高，粒徑為1 μm以下的顆粒物所占百分數越低.但從圖4也可以看出，隨著煙氣流速的增大，1 μm以下顆粒物所占百分數減小的幅度有限，煙氣流速14 m/s時的顆粒物數量百分數只比煙氣流速10 m/s時減小了0.61%.另一方面，由于煙氣流速的增大，顆粒物在凝并區的停留時間縮短，凝并區顆粒物的瞬時濃度降低，減小了顆粒物繼續碰撞凝并成為超大顆粒物的概率，因此，顆粒物碰撞凝并成的顆粒多集中在1～<2.5 μm和10～<20 μm 2個區間，而在2.5～<5 μm、5～<10 μm以及20 μm以上3個區間，顆粒物數量百分數隨煙氣流速的增大而減小.

4 結 論

(1) 在所模擬的煙氣流速范圍內，凝并器入口煙氣流速越高，凝并區的湍流強度和渦量越大，但顆粒物在凝并區內的停留時間也越短，當煙氣流速由10 m/s增大到14 m/s時，停留時間在0.1 s以下的顆粒物數量百分數由近乎零增大到超過50%.

(2) 提高凝并器入口煙氣流速，有利于減少細顆粒物的數量，但減少的幅度有限，煙氣流速14 m/s時粒徑在0.1～<1 μm之間的顆粒物數量百分數只比煙氣流速10 m/s時減小了0.61%.

(3) 凝并器入口煙氣流速越大，碰撞凝并形成的顆粒物粒徑也越小，不利于形成超大顆粒物，因此并不是煙氣流速越大，湍流凝并的效果就越好，通過對比模擬數據與實驗結果，可以認為在電廠滿負荷運行時，靜電除塵器前煙道的煙氣流速在10～14 m/s的條件下,凝并器入口煙氣流速的提高對湍流凝并的負面效果大于正面效果.

[1] 韓光. 超細粉塵凝并裝置中產渦段優化布置的研究[D]. 保定: 華北電力大學, 2013.

[2] 樊建人, 姚軍, 張新育, 等. 氣固兩相流中顆粒-顆粒隨機碰撞新模型[J]. 工程熱物理學報, 2001, 22(5): 629-632.

FAN Jianren, YAO Jun, ZHANG Xinyu, et al. Modeling particle-to-particle interactions in gas-solid flows[J]. Journal of Engineering Thermophysics, 2001, 22(5): 629-632.

[3] 劉忠, 劉含笑, 馮新新, 等. 湍流聚并器流場和顆粒運動軌跡模擬[J]. 電機工程學報, 2012, 32(14): 71-75.

LIU Zhong, LIU Hanxiao, FENG Xinxin, et al. Simulation for the flow field of the turbulence coalescence device and the trajectory of particles[J]. Proceedings of the CSEE, 2012, 32(14): 71-75.

[4] 鄭力銘. ANSYS Fluent 15.0流體計算從入門到精通[M]. 北京: 電子工業出版社, 2015.

[5] SPALART P R, DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195.

[6] 丁舉春, 吳宗成, 鞠勝軍. 分離渦模擬方法的研究[C]//北京力學會第18 屆學術年會論文集. 北京: 北京力學會, 2012: 47-48.

[7] O'ROURKE P J, BRACCO F V. Modeling of drop interactions in thick sprays and a comparison with experiments[J]. Proceedings of the Institution of Mechanical Engineers, 1980,194(9): 101-106.

[8] 陳亞偉, 熊揚恒, 周建龍, 等. 凝并元件結構優化對氣固兩相流流場及顆粒凝并效果的影響[J]. 熱力發電, 2016, 45(1): 60-64.

CHEN Yawei, XIONG Yangheng, ZHOU Jianlong, et al. Influence of coagulation element structure optimization on the gas-solid two-phase flow field and particulate coagulation[J]. Thermal Power Generation, 2016, 45(1): 60-64.

[9] LUO Kun, FAN Jianren, CEN Kefa. Local-focusing phenomenon and turbulence modulation in particle-laden turbulent jets[J]. Physics Letters A, 2005, 343(1/2/3): 190-198.

[10] 施學貴, 徐旭常, 馮俊凱. 顆粒在湍流氣流中運動的受力分析[J]. 工程熱物理學報, 1989, 10(3): 320-325.

SHI Xuegui, XU Xuchang, FENG Junkai. The analysis of forces on particles moving in turbulent flow[J]. Journal of Engineering Thermophysics, 1989, 10(3): 320-325.

[11] 劉含笑. 燃煤超細顆粒物渦聚并數值模擬[D]. 保定: 華北電力大學, 2012.

[12] 劉含笑, 姚宇平, 酈建國. 凝聚器二維單擾流柱流場中顆粒凝并模擬[J]. 動力工程學報, 2015, 35(4): 292-297.

LIU Hanxiao, YAO Yuping, LI Jianguo. Coagulating simulation of particles in flow field of coagulator 2D single turbulence column[J]. Journal of Chinese Society of Power Engineering, 2015, 35(4): 292-297.

Effects of Flue Gas Velocity on the Formation of Turbulent Vortex and the Coagulation of Fine Particles

CHENYawei1,XIONGYangheng1,PANZuming2,ZHOUJianlong1,ZHOUMeng1

(1.School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China; 2. Wuhan Likang Energy Co., Ltd., Wuhan 430000, China)

A simulation was conducted on the collision and coagulation of particles flowing in the flue duct before electrostatic precipitator of a power plant under full load conditions using Eulerian-Lagrangian method and O'Rouekr collision model. Results show that, the higher the flue gas velocity is at the coagulator inlet, the larger the turbulent intensity and vorticity will be, which is favorable for the reduction of small particles, but in a limited degree; whereas, the higher the flue gas velocity is at the coagulator inlet, the shorter the residence time of particles will be in the coagulation zone, and the smaller the particles will be formed by collision and coagulation, which is unfavorable for the formation of large particles. Within the common range of flue gas velocity in a power plant, the increase of flue gas velocity at the coagulator inlet has a negative impact stronger than positive impact on the turbulence coagulation.

fine particles; flue gas velocity; particle residence time; turbulence coagulation

2016-05-19

2016-07-14

陳亞偉(1990-)，男，河南輝縣人，碩士研究生，研究方向為火力發電超低排放系統建模、優化與控制. 電話(Tel.):18672755830；E-mail:cyw711@163.com.

1674-7607(2017)05-0408-05

X513

A 學科分類號：610.30