徑向換能型超聲波電機(jī)定子振動(dòng)模型

蔣春容 董曉霄 張津楊 金 龍

(1.南京工程學(xué)院電力工程學(xué)院 南京 211167 2.東南大學(xué)電氣工程學(xué)院 南京 210096)

?

徑向換能型超聲波電機(jī)定子振動(dòng)模型

蔣春容1董曉霄2張津楊1金 龍2

(1.南京工程學(xué)院電力工程學(xué)院 南京 211167 2.東南大學(xué)電氣工程學(xué)院 南京 210096)

提出了一種彈性葉片式徑向換能型超聲波電機(jī)，分析了電機(jī)的結(jié)構(gòu)與工作原理，建立了定子徑向自由振動(dòng)和受迫振動(dòng)的解析模型，同時(shí)，為了進(jìn)行對(duì)比驗(yàn)證，建立了定子振動(dòng)的有限元模型進(jìn)行模態(tài)分析和諧響應(yīng)分析。分別采用兩種模型計(jì)算得到了定子一階徑向自由振動(dòng)的頻率和在外加電壓激勵(lì)下受迫振動(dòng)的徑向振幅，兩種模型的理論計(jì)算結(jié)果接近。采用阻抗特性分析儀測(cè)量了定子一階徑向自由振動(dòng)的頻率，并采用激光測(cè)振儀測(cè)量了定子外側(cè)表面質(zhì)點(diǎn)在外加電壓作用下徑向振動(dòng)的振幅，將實(shí)驗(yàn)測(cè)試結(jié)果與理論計(jì)算結(jié)果進(jìn)行對(duì)比，二者基本吻合。實(shí)驗(yàn)測(cè)試結(jié)果驗(yàn)證了所建立的定子振動(dòng)的解析模型和有限元模型的有效性。最后，制作了原理性樣機(jī)，驗(yàn)證了所提出的徑向換能型超聲波電機(jī)動(dòng)作原理的可行性。

超聲波電機(jī) 徑向換能 定子振動(dòng) 解析模型 有限元模型

0 引言

超聲波電機(jī)結(jié)構(gòu)設(shè)計(jì)靈活多變，利用不同的壓電陶瓷極化形式和彈性體的振動(dòng)模態(tài)，可以構(gòu)造出不同結(jié)構(gòu)的超聲波電機(jī)。迄今為止，研究最為成熟的是環(huán)形行波超聲波電機(jī)[1，2]，它利用了定子的彎曲振動(dòng)模態(tài)。此外，還有利用定子的縱向振動(dòng)、扭轉(zhuǎn)振動(dòng)等模態(tài)或多種模態(tài)復(fù)合的方式構(gòu)造超聲波電機(jī)[3-6]，但利用定子的徑向伸縮振動(dòng)構(gòu)造超聲波電機(jī)的研究較少。本文提出一種利用定子徑向振動(dòng)換能方式構(gòu)造的超聲波電機(jī)。

超聲波電機(jī)的能量轉(zhuǎn)換分為兩個(gè)過(guò)程：第一個(gè)過(guò)程是將高頻交流電轉(zhuǎn)換為定子的超聲振動(dòng)；第二個(gè)過(guò)程是通過(guò)摩擦傳動(dòng)將定子的超聲振動(dòng)轉(zhuǎn)換為轉(zhuǎn)子的旋轉(zhuǎn)運(yùn)動(dòng)。超聲波電機(jī)第一個(gè)能量轉(zhuǎn)換過(guò)程是考慮壓電材料逆壓電效應(yīng)的定子振動(dòng)特性的研究，對(duì)電機(jī)的設(shè)計(jì)、優(yōu)化及控制都具有重要作用[7]。目前，國(guó)內(nèi)外學(xué)者對(duì)超聲波電機(jī)定子振動(dòng)特性展開(kāi)了較多研究。P.Hagedorn等[8]、J.L.Pons 等[9]建立了環(huán)形行波超聲波電機(jī)定子的振動(dòng)模型，采用數(shù)值計(jì)算方法求解定子的振動(dòng)方程；Y.Nakagawa等[10]、Sun Dong等[11]、Yao Zhiyuan等[12]以及王光慶等[13]建立了行波超聲波電機(jī)定子振動(dòng)的解析模型，分析了定子的振動(dòng)特性；Liu Yingxiang等[14]、夏長(zhǎng)亮等[15]、莫岳平等[16]以及A.M.Morega等[17]基于有限元法分析了行波超聲波電機(jī)定子的結(jié)構(gòu)動(dòng)力學(xué)特性。現(xiàn)有的對(duì)超聲波電機(jī)定子振動(dòng)特性的研究多數(shù)是基于較為成熟的行波超聲波電機(jī)，而對(duì)采用徑向振動(dòng)換能方式的超聲波電機(jī)有關(guān)機(jī)理的研究相對(duì)欠缺。

在超聲波電機(jī)定子振動(dòng)模型的研究方法中，多采用解析法或有限元法。采用有限元法分析時(shí)，可以考慮復(fù)雜的定子結(jié)構(gòu)，計(jì)算結(jié)果準(zhǔn)確；缺點(diǎn)是每修改一次電機(jī)的結(jié)構(gòu)，都需要重新建模，計(jì)算比較費(fèi)時(shí)。采用解析法分析時(shí)，往往需要對(duì)復(fù)雜結(jié)構(gòu)的定子作一定的簡(jiǎn)化假設(shè)，否則存在建模和求解困難的問(wèn)題，但該方法可以節(jié)省計(jì)算時(shí)間。

本文提出了一種彈性葉片式徑向換能型超聲波電機(jī)，分析了電機(jī)的結(jié)構(gòu)與工作原理，采用解析法建立了電機(jī)定子的徑向振動(dòng)模型，以便于快速地分析計(jì)算電機(jī)的振動(dòng)特性，節(jié)省計(jì)算時(shí)間。同時(shí)，為了進(jìn)行對(duì)比驗(yàn)證，基于有限元計(jì)算軟件建立了定子振動(dòng)的有限元模型。分別采用兩種模型分析了定子的徑向自由振動(dòng)和在外加電壓激勵(lì)下的受迫振動(dòng)。實(shí)驗(yàn)測(cè)量了定子的阻抗-頻率特性以及在外加電壓作用下定子的徑向振幅，驗(yàn)證了定子自由振動(dòng)和受迫振動(dòng)的理論分析結(jié)果。最后，制作了原理性樣機(jī)，驗(yàn)證了所提出的徑向換能型超聲波電機(jī)動(dòng)作原理的可行性。

1 電機(jī)結(jié)構(gòu)與工作原理

徑向換能型超聲波電機(jī)結(jié)構(gòu)如圖1所示。電機(jī)的定子由壓電陶瓷、彈性薄圓環(huán)和彈性葉片組成，壓電陶瓷外側(cè)面通過(guò)膠粘的方式與彈性薄圓環(huán)內(nèi)側(cè)面連接，壓電陶瓷的體積占整個(gè)定子體積的90%以上。彈性葉片沿周向均勻布置在彈性薄圓環(huán)的外側(cè)，并與彈性薄圓環(huán)徑向成30°夾角。彈性葉片與轉(zhuǎn)子接觸時(shí)產(chǎn)生一定的彈性彎曲變形。壓電陶瓷極化方向?yàn)檩S向，即厚度方向。給壓電陶瓷上下表面施加特定頻率的單相交流電，激發(fā)出壓電陶瓷和彈性薄圓環(huán)的一階徑向伸縮振動(dòng)，彈性葉片一方面隨彈性薄圓環(huán)一起作徑向運(yùn)動(dòng)，另一方面在徑向伸縮振動(dòng)帶動(dòng)下與轉(zhuǎn)子接觸時(shí)產(chǎn)生周期性的橫向彎曲變形，進(jìn)而在彈性葉片端點(diǎn)合成橢圓運(yùn)動(dòng)，推動(dòng)與之接觸的轉(zhuǎn)子旋轉(zhuǎn)，并由轉(zhuǎn)子帶動(dòng)轉(zhuǎn)軸輸出功率。

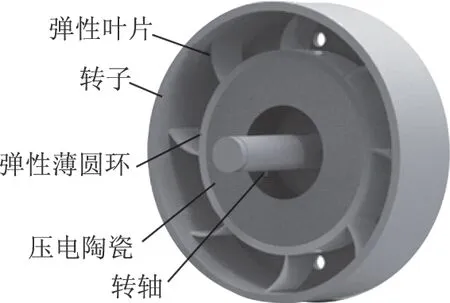
圖1 超聲波電機(jī)結(jié)構(gòu)Fig.1 Structure of the ultrasonic motor

2 定子振動(dòng)解析模型

2.1 定子的自由振動(dòng)

考慮到定子絕大部分體積為壓電陶瓷，彈性薄圓環(huán)的徑向厚度(0.5 mm)遠(yuǎn)小于壓電陶瓷的徑向厚度(5 mm)，而彈性葉片主要實(shí)現(xiàn)彎曲變形，因此在分析定子的徑向振動(dòng)時(shí)，忽略彈性薄圓環(huán)和彈性葉片的影響，建立以壓電陶瓷為代表的等效定子的振動(dòng)模型，如圖2所示。壓電陶瓷內(nèi)側(cè)面為自由狀態(tài)。壓電陶瓷外側(cè)面與彈性薄圓環(huán)之間采用膠粘的方式連接，施加在壓電陶瓷上的徑向預(yù)應(yīng)力非常有限，且膠粘劑的彈性模量遠(yuǎn)低于壓電陶瓷的彈性模量，因此可近似認(rèn)為壓電陶瓷外側(cè)面也為自由狀態(tài)。

圖2 等效定子Fig.2 The equivalent stator

根據(jù)圓環(huán)的對(duì)稱性，采用柱坐標(biāo)系(r，θ，z)最為方便。在柱坐標(biāo)系下，等效定子圓環(huán)(也即壓電陶瓷圓環(huán))徑向振動(dòng)的動(dòng)力學(xué)方程為

(1)

式中，Trr和Tθθ為正應(yīng)力；Trθ和Trz為切應(yīng)力；ur為徑向位移；ρ為壓電陶瓷的密度；Fr為外加徑向作用力。為簡(jiǎn)化分析，假設(shè)定子圓環(huán)作單純的徑向振動(dòng)，則除了徑向位移ur不為零，其他位移均為零，即切向位移uθ=0，軸向位移uz=0。單純的徑向振動(dòng)并不引起剪切變形，因此所有的切應(yīng)力和切應(yīng)變均為零[18]。在上述假設(shè)下，由式(1)可得到定子徑向振動(dòng)的簡(jiǎn)化微分方程為

(2)

當(dāng)分析定子的自由振動(dòng)時(shí)，外加作用力Fr=0。在柱坐標(biāo)系中，定子徑向振動(dòng)的應(yīng)變與位移之間的關(guān)系可表示為

(3)

(4)

式中，Srr和Sθθ分別為徑向和切向正應(yīng)變。對(duì)于沿軸向方向極化的壓電陶瓷圓環(huán)，描述其電學(xué)量和力學(xué)量的壓電方程為

(5)

(6)

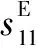
(7)

(8)

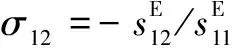
(9)

(10)

將式(9)和式(10)代入式(2)化簡(jiǎn)可得定子徑向自由振動(dòng)的微分方程為

(11)

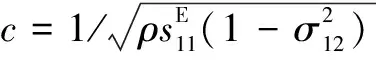
ur=R(r)ejωt

(12)

將式(12)代入式(11)可得

(13)

式中，k=ω/c。式(13)是一個(gè)貝塞爾微分方程，其解可表示為[19]

R(r)=AJ1(kr)+BN1(kr)

(14)

式中，J1(kr)和N1(kr)分別為一階貝塞爾函數(shù)和諾依曼函數(shù)；A和B為待定常數(shù)，由邊界條件決定。

將式(14)代入式(12)可得定子圓環(huán)徑向自由振動(dòng)的解為

ur=[AJ1(kr)+BN1(kr)]ejωt

(15)

將式(15)代入式(3)和式(4)，并利用貝塞爾函數(shù)和諾依曼函數(shù)的特性化簡(jiǎn)，可得正應(yīng)變Srr和Sθθ分別為

B[krN0(kr)-N1(kr)]}ejωt

(16)

(17)

式中，J0(kr)和N0(kr)分別為零階貝塞爾函數(shù)和諾依曼函數(shù)。將式(16)和式(17)代入式(7)可得自由振動(dòng)定子的徑向正應(yīng)力為

(18)

利用壓電陶瓷內(nèi)徑r=r1和外徑r=r2處應(yīng)力為零的自由邊界條件，可得

A[kr1J0(kr1)-(1-σ12)J1(kr1)]+

B[kr1N0(kr1)-(1-σ12)N1(kr1)]=0

(19)

A[kr2J0(kr2)-(1-σ12)J1(kr2)]+

B[kr2N0(kr2)-(1-σ12)N1(kr2)]=0

(20)

若要使系數(shù)A和B有非零解，則它們的系數(shù)行列式必為零，即

[kr1J0(kr1)-(1-σ12)J1(kr1)]·

[kr2N0(kr2)-(1-σ12)N1(kr2)]=

[kr1N0(kr1)-(1-σ12)N1(kr1)]·

[kr2J0(kr2)-(1-σ12)J1(kr2)]

(21)

由式(21)可求得k的值，進(jìn)而確定定子徑向振動(dòng)的共振頻率及其對(duì)應(yīng)的振動(dòng)模態(tài)。假設(shè)k=k1為定子一階徑向振動(dòng)所對(duì)應(yīng)的解，則一階徑向振動(dòng)的角頻率為

(22)

顯然，一階徑向振動(dòng)的頻率f1=ω1/(2π)。對(duì)應(yīng)于f1的一階徑向振動(dòng)模態(tài)為

R1(r)=J1(k1r)+A1N1(k1r)

(23)

其中

(24)

2.2 定子的受迫振動(dòng)

給壓電陶瓷的上下表面施加激勵(lì)電壓，定子作受迫振動(dòng)，其振動(dòng)方程為

(25)

式中，c1為阻尼系數(shù)；f(r，t)為外加激勵(lì)電壓作用產(chǎn)生的附加項(xiàng)。當(dāng)外加激勵(lì)電壓為Umejωt時(shí)，式(2)中的外加作用力Fr為[20]

(26)

式中，h為定子的軸向厚度。將式(26)代入式(2)并化簡(jiǎn)后與式(25)對(duì)比可得

(27)

方程(25)的解可用模態(tài)疊加的方法得到

(28)

式中，Rn(r)為定子的第n階徑向振動(dòng)模態(tài)，且Rn(r)滿足式(13)的關(guān)系；qn(t)為第n階模態(tài)參與因子。為了求得qn(t)，將式(28)代入式(25)并利用式(13)的關(guān)系化簡(jiǎn)可得

(29)

式中，ωn為對(duì)應(yīng)于Rn(r)振型的角頻率。將式(29)左右兩邊同時(shí)乘以第m階徑向振型函數(shù)Rm(r)，并從r1至r2對(duì)變量r積分，利用振型函數(shù)的正交性可得

(30)

式中，ζn為阻尼比，ζn=c1c2/(2ωn)。定子工作在一階徑向振動(dòng)模態(tài)，其他模態(tài)與工作模態(tài)頻率相差很遠(yuǎn)，可忽略其他模態(tài)的影響，因此，受迫振動(dòng)的解可簡(jiǎn)化為只考慮n=1的情況，即

ur=q1(t)R1(r)

(31)

為求得q1(t)，在式(30)中取n=1，并將式(27)代入，化簡(jiǎn)可得

(32)

其中

(33)

將式(23)代入式(33)，并利用數(shù)值計(jì)算方法可求得Q的值，進(jìn)而可以得到q1(t)的解

q1(t)=Xej(ωt-φ)

(34)

其中

(35)

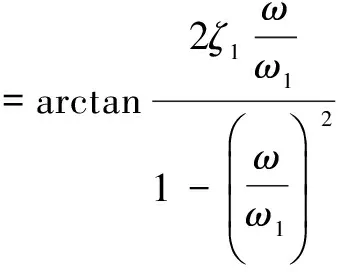
(36)

至此可得定子受迫振動(dòng)響應(yīng)的解為

ur=X[J1(k1r)+A1N1(k1r)]ej(ωt-φ)

(37)

受迫振動(dòng)的徑向振幅為

urmax=X[J1(k1r)+A1N1(k1r)]

(38)

3 定子振動(dòng)有限元模型

為了對(duì)所提出的解析模型進(jìn)行對(duì)比驗(yàn)證，建立了徑向換能型超聲波電機(jī)定子振動(dòng)的有限元模型，求得定子振動(dòng)的數(shù)值解。

根據(jù)定子振動(dòng)所滿足的有限元方程[16]，采用有限元計(jì)算軟件ANSYS(ANSYS14.0)建立定子振動(dòng)的三維有限元模型，對(duì)定子分別進(jìn)行模態(tài)分析和諧響應(yīng)分析，以得到定子徑向自由振動(dòng)和受迫振動(dòng)的數(shù)值解。所建立的有限元模型如圖3所示。有限元模型中同樣忽略了彈性薄圓環(huán)和彈性葉片的影響。由于要考慮壓電陶瓷的逆壓電效應(yīng)，因此選擇耦合場(chǎng)分析單元SOLID5(八節(jié)點(diǎn)六面體單元)對(duì)定子進(jìn)行網(wǎng)格劃分，劃分單元數(shù)為6 000個(gè)，節(jié)點(diǎn)數(shù)為7 260個(gè)。定子的內(nèi)外表面均為自由邊界條件。定子模態(tài)分析時(shí)，在上下表面節(jié)點(diǎn)施加電壓為零的約束條件[14]，所選擇的求解方法為BlockLanczos法。諧響應(yīng)分析時(shí)在定子上下表面節(jié)點(diǎn)施加特定的激勵(lì)電壓，設(shè)置阻尼比常量，并選擇Full法進(jìn)行求解。

圖3 定子有限元模型Fig.3 Finite element model of the stator

4 仿真計(jì)算與實(shí)驗(yàn)結(jié)果分析

計(jì)算所用的徑向換能型超聲波電機(jī)的參數(shù)見(jiàn)表1，壓電陶瓷及粘接好的定子樣機(jī)如圖4所示，所采用的壓電陶瓷的型號(hào)為P-81。

表1 徑向換能型超聲波電機(jī)的參數(shù)

圖4 定子樣機(jī)Fig.4 Prototype of the stator

4.1 自由振動(dòng)分析

首先應(yīng)用所提出的解析模型和在ANSYS中建立的有限元模型，計(jì)算定子徑向自由振動(dòng)的頻率。解析模型計(jì)算得到的定子一階徑向自由振動(dòng)的頻率為77.34 kHz，有限元模型計(jì)算得到的一階徑向自由振動(dòng)的頻率為76.58 kHz，兩種模型的理論計(jì)算結(jié)果接近。定子一階徑向自由振動(dòng)的振型如圖5所示。圖5中，粗實(shí)線代表定子未變形前的狀態(tài)，其余的代表定子發(fā)生一階徑向振動(dòng)擴(kuò)張后的狀態(tài)。

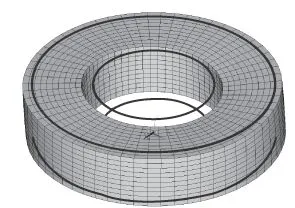
圖5 定子一階徑向自由振動(dòng)的振型Fig.5 First order radial vibration mode of the stator

表2 自由振動(dòng)分析結(jié)果

4.2 受迫振動(dòng)分析

給壓電陶瓷上下表面通以特定頻率的正弦交流電，激發(fā)出定子的一階徑向振動(dòng)。應(yīng)用解析模型對(duì)定子一階徑向振動(dòng)的振幅urmax進(jìn)行計(jì)算，同時(shí)利用有限元模型進(jìn)行諧響應(yīng)分析。當(dāng)激勵(lì)電壓幅值Um為85 V、頻率f為共振頻率f1時(shí)，定子不同半徑處質(zhì)點(diǎn)的徑向振幅如圖7所示。由圖7可見(jiàn)，解析模型和有限元模型計(jì)算結(jié)果接近，越遠(yuǎn)離圓心的質(zhì)點(diǎn)，一階徑向振動(dòng)的振幅越小。

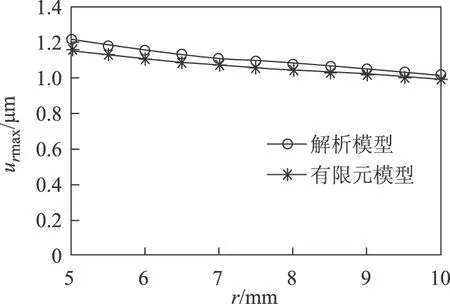
圖7 不同半徑處質(zhì)點(diǎn)的徑向振幅Fig.7 Radial vibration amplitudes of particles at different radius

當(dāng)外加激勵(lì)電壓的頻率f變化時(shí)，定子振幅隨之變化。取壓電陶瓷外側(cè)表面質(zhì)點(diǎn)，即半徑r=10 mm處的質(zhì)點(diǎn)為例，其徑向振幅隨頻率變化趨勢(shì)如圖8所示。圖8中，外加激勵(lì)電壓的幅值Um保持85 V不變，分別應(yīng)用解析模型和有限元模型進(jìn)行計(jì)算，橫坐標(biāo)取激勵(lì)頻率f與共振頻率f1的比值，以此來(lái)分析激勵(lì)頻率在共振頻率附近變化時(shí)定子振幅的變化。由圖8可知，兩種模型的理論計(jì)算結(jié)果基本一致。在共振頻率點(diǎn)，定子徑向振幅達(dá)到最大值，離共振頻率點(diǎn)越遠(yuǎn)，徑向振幅越小。

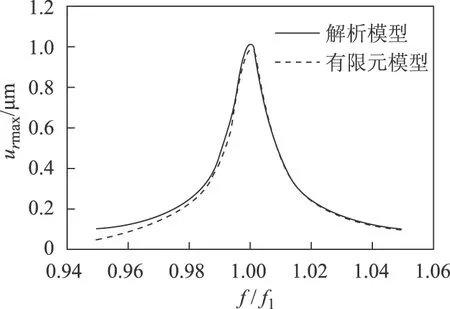
圖8 不同頻率下質(zhì)點(diǎn)的徑向振幅Fig.8 Radial vibration amplitudes of particles under different frequencies

應(yīng)用激光測(cè)振儀(德國(guó)Polytechnic公司，PSV-400-M2)對(duì)定子受迫振動(dòng)的徑向振幅進(jìn)行測(cè)量，測(cè)量方法如圖9所示。定子放置在兩個(gè)彈性絕緣墊片之間，并由上下兩個(gè)固定盤(pán)固定，上下兩個(gè)固定盤(pán)之間施加一定的預(yù)壓力，這樣既保證了測(cè)量過(guò)程中定子不發(fā)生移位，又使得定子的徑向振動(dòng)盡量不受影響。激光射線沿徑向照射到定子的外側(cè)表面上，以保證照射方向與徑向振動(dòng)方向一致。

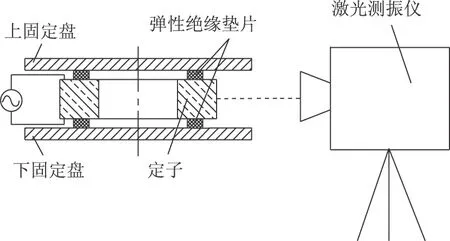
圖9 徑向振動(dòng)實(shí)驗(yàn)測(cè)量方法Fig.9 Experimental setup for measuring radial vibration

首先測(cè)量如圖4a所示的未粘接彈性薄圓環(huán)的定子受迫振動(dòng)的振幅。在壓電陶瓷上下表面施加幅值為85 V的正弦交流電，其頻率為共振頻率f1，測(cè)量得到未粘接彈性薄圓環(huán)的定子外側(cè)表面質(zhì)點(diǎn)的徑向振幅，如圖10a所示，徑向振幅為1.103 μm。同時(shí)，采用同樣的測(cè)試方法測(cè)量了如圖4b所示的粘接彈性薄圓環(huán)后的定子外側(cè)表面質(zhì)點(diǎn)在共振頻率點(diǎn)的徑向振幅，結(jié)果如圖10b所示，定子外側(cè)表面質(zhì)點(diǎn)的徑向振幅為0.913 μm。

圖10 徑向振幅測(cè)量結(jié)果Fig.10 Measurements of radial vibration amplitude

為便于進(jìn)行對(duì)比，將理論計(jì)算和實(shí)驗(yàn)測(cè)量得到的共振頻率點(diǎn)的徑向振幅一并列于表3中。由表3可知，兩種模型的理論計(jì)算結(jié)果與實(shí)驗(yàn)測(cè)量結(jié)果相吻合，驗(yàn)證了所提出的解析模型和ANSYS中建立的有限元模型的有效性。粘接了彈性薄圓環(huán)后，定子外側(cè)表面測(cè)量點(diǎn)的半徑比未粘接彈性薄圓環(huán)的定子表面測(cè)量點(diǎn)的半徑大，因此振幅略有減小。另外，由于粘合劑的作用，也使得徑向振幅有一定程度的減小。

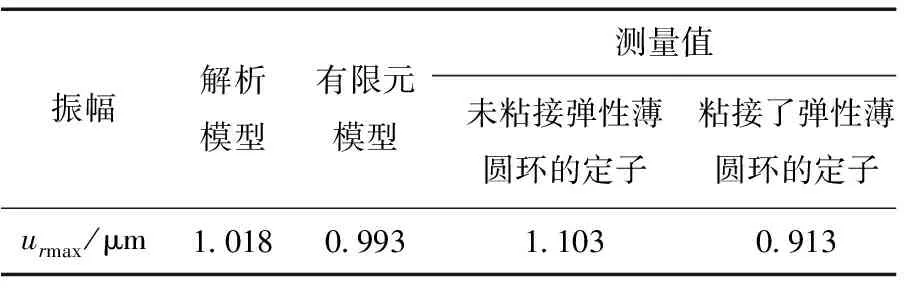
表3 受迫振動(dòng)分析結(jié)果

另外，還測(cè)試了定子一階徑向振動(dòng)模態(tài)下的縱向(軸向)振幅。以粘接了彈性薄圓環(huán)的定子為測(cè)試對(duì)象，施加電壓幅值85 V，在共振頻率點(diǎn)時(shí)，縱向振幅為0.147 μm，相比徑向振幅，縱向振幅要小得多。

4.3 原理性樣機(jī)

最后，為驗(yàn)證徑向換能型超聲波電機(jī)動(dòng)作原理的可行性，制作了電機(jī)樣機(jī)，如圖11所示，電機(jī)直徑為32 mm，厚度為13 mm。給電機(jī)通以幅值為85 V、頻率為76 kHz的正弦交流電時(shí)，電機(jī)的空載轉(zhuǎn)速為45 r/min，堵轉(zhuǎn)轉(zhuǎn)矩為0.17 N·m。

圖11 電機(jī)樣機(jī)Fig.11 Prototype of ultrasonic motor

5 結(jié)論

本文提出了一種彈性葉片式徑向換能型超聲波電機(jī)，建立了定子徑向自由振動(dòng)和受迫振動(dòng)的解析模型，同時(shí)，為進(jìn)行對(duì)比驗(yàn)證，基于有限元計(jì)算軟件建立了定子振動(dòng)的有限元模型進(jìn)行模態(tài)分析和諧響應(yīng)分析。分別采用兩種模型計(jì)算得到了定子一階徑向自由振動(dòng)的頻率和外加激勵(lì)電壓作用下的徑向振幅，兩種模型的理論計(jì)算結(jié)果接近。計(jì)算結(jié)果表明：在相同的外加激勵(lì)電壓作用下，越遠(yuǎn)離圓心的質(zhì)點(diǎn)，一階徑向振動(dòng)振幅越小；在共振頻率點(diǎn)，定子徑向振幅達(dá)到最大值，離共振頻率點(diǎn)越遠(yuǎn)，徑向振幅越小。采用阻抗特性分析儀測(cè)量了粘接彈性薄圓環(huán)前后定子一階徑向自由振動(dòng)的頻率，實(shí)驗(yàn)測(cè)試結(jié)果與定子自由振動(dòng)的理論計(jì)算結(jié)果相吻合，測(cè)量結(jié)果也表明粘接彈性薄圓環(huán)前后定子阻抗-頻率特性曲線并無(wú)明顯變化，證明模型中忽略彈性薄圓環(huán)和彈性葉片影響的簡(jiǎn)化假設(shè)是合理的。采用激光測(cè)振儀測(cè)量了粘接彈性薄圓環(huán)前后定子外側(cè)表面質(zhì)點(diǎn)在共振頻率點(diǎn)的徑向振幅，并與定子受迫振動(dòng)的理論計(jì)算結(jié)果進(jìn)行對(duì)比，二者基本吻合。實(shí)驗(yàn)測(cè)試結(jié)果驗(yàn)證了所建立的定子振動(dòng)解析模型和有限元模型的有效性。最后制作了徑向換能型超聲波電機(jī)樣機(jī)，驗(yàn)證了所提出的電機(jī)動(dòng)作原理的可行性。

定子徑向高頻振動(dòng)的產(chǎn)生是超聲波電機(jī)能量轉(zhuǎn)換的第一個(gè)過(guò)程，還需要通過(guò)接觸摩擦將定子的高頻振動(dòng)轉(zhuǎn)換為轉(zhuǎn)子的旋轉(zhuǎn)運(yùn)動(dòng)，完成第二個(gè)能量轉(zhuǎn)換過(guò)程。因此，本文下一步的研究工作是考慮彈性葉片與轉(zhuǎn)子接觸產(chǎn)生彈性彎曲變形，建立彈性葉片與轉(zhuǎn)子之間的接觸摩擦模型，進(jìn)而得到推動(dòng)轉(zhuǎn)子旋轉(zhuǎn)的轉(zhuǎn)矩及電機(jī)的輸出性能。另外，目前研究的電機(jī)樣機(jī)直徑較小，輸出轉(zhuǎn)矩有待進(jìn)一步提高，可研究直徑更大、利用徑向換能的大力矩超聲波電機(jī)。

[1] Peng Taijiang，Shi Hongyan，Liang Xiong，et al.Experimental investigation on sandwich structure ring-type ultrasonic motor[J].Ultrasonics，2015，56：303-307.

[2] 陸旦宏，胡敏強(qiáng)，金龍，等.基于空間調(diào)相的環(huán)形行波超聲波電機(jī)的幅相控制[J].電工技術(shù)學(xué)報(bào)，2014，29(3)：132-142. Lu Danhong，Hu Minqiang，Jin Long，et al.Amplitude-phase control of ring-type travelling-wave ultrasonic motors based on space phase modulation[J].Transactions of China Electrotechnical Society，2014，29(3)：132-142.

[3] 沈潤(rùn)杰，王波，郭吉豐，等.微型斜齒超聲波電機(jī)的研究[J].振動(dòng)工程學(xué)報(bào)，2007，20(5)：543-548. Shen Runjie，Wang Bo，Guo Jifeng.Study on skew teeth micro ultrasonic motor[J].Journal of Vibration Engineering，2007，20(5)：543-548.

[4] 王光慶，岳玉秋，展永政.縱-彎復(fù)合旋轉(zhuǎn)式超聲波電動(dòng)機(jī)的優(yōu)化設(shè)計(jì)與性能分析[J].電工技術(shù)學(xué)報(bào)，2015，30(22)：33-41. Wang Guangqing，Yue Yuqiu，Zhan Yongzheng. Optimum design and performances analysis of the longitudinal-bending hybrid rotating type ultrasonic motor[J].Transactions of China Electrotechnical Society，2015，30(22)：33-41.

[5] 王劍，郭吉豐.一種中空短柱徑向-扭轉(zhuǎn)振動(dòng)復(fù)合型超聲波電動(dòng)機(jī)[J].電工技術(shù)學(xué)報(bào)，2009，24(10)：6-11. Wang Jian，Guo Jifeng.A radial-torsional vibration hybrid type ultrasonic motor with hollow and short cylindrical structure[J].Transactions of China Electrotechnical Society，2009，24(10)：6-11.

[6] Sheng Mingwei，Chen Weishan，Liu Junkao，et al.Study and test of a double-rotor ultrasonic motor with symmetrical longitudinal-torsional converter[C]//18thIEEE International Symposium on the Applications of Ferroelectrics，Xian，China，2009.

[7] Shi Jingzhuo，You Dongmei.Characteristic model of travelling wave ultrasonic motor[J].Ultrasonics，2014，54(2)：725-730.

[8] Hagedorn P，Wallashek J，Konrad W.Travelling wave ultrasonic motors，part II：a numerical method for the flexural vibrations of the stator[J].Journal of Sound and Vibration，1993，168(1)：115-122.

[9] Pons J L，Rodriguez H，Ceres R，et al.Novel modeling technique for the stator of traveling wave ultrasonic motors[J].IEEE Transactions on Ultrasonics，F(xiàn)erroelectrics，and Frequency Control，2003，50(11)：1429-1435.

[10]Nakagawa Y，Saito A，Maeno T.Nonlinear dynamic analysis of traveling wave-type ultrasonic motors[J].IEEE Transactions on Ultrasonics，F(xiàn)erroelectrics，and Frequency Control，2008，55(3)：717-725.

[11]Sun Dong，Liu Jinbo，Ai Xing.Modeling and performance evaluation of traveling wave piezoelectric ultrasonic motors with analytical method[J].Sensors and Actuators A：Physical，2002，100(1)：84-93.

[12]Yao Zhiyuan，Zhao Chunsheng，Zeng Jinsong，et al.Analytical solution on the non-linear vibration of a traveling wave ultrasonic motor[J].Journal of Electroceramics，2008，20(3-4)：251-258.

[13]王光慶，陸國(guó)麗，郭吉豐.基于能量等效的行波型超聲波電動(dòng)機(jī)解析模型[J].機(jī)械工程學(xué)報(bào)，2008，44(2)：74-81. Wang Guangqing，Lu Guoli，Guo Jifeng.Analytical model of traveling-wave type ultrasonic motor based on the energy equivalent method[J].Journal of Mechanical Engineering，2008，44(2)：74-81.

[14]Liu Yingxiang，Liu Junkao，Chen Weishan.A cylindrical traveling wave ultrasonic motor using a circumferential composite transducer[J].IEEE Transactions on Ultrasonics，F(xiàn)erroelectrics，and Frequency Control，2011，58(11)：2397-2404.

[15]夏長(zhǎng)亮，鄭堯，史婷娜，等.行波接觸型超聲波電機(jī)定子振動(dòng)有限元分析[J].中國(guó)電機(jī)工程學(xué)報(bào)，2001，21(2)：25-28，32. Xia Changliang，Zheng Yao，Shi Tingna，et al.FEM analysis on stator vibration of traveling wave type contact ultrasonic motor[J].Proceedings of the CSEE，2001，21(2)：25-28，32.

[16]莫岳平，胡敏強(qiáng)，徐志科，等.超聲波電機(jī)振動(dòng)模態(tài)有限元分析[J].中國(guó)電機(jī)工程學(xué)報(bào)，2002，22(11)：92-96. Mo Yueping，Hu Minqiang，Xu Zhike，et al. The finite element analysis on the vibration mode of ultrasonic motor[J].Proceedings of the CSEE，2002，22(11)：92-96.

[17]Morega A M，Robello G，Morega M，et al.Numerical study of the stator motion in a piezoelectric ultrasonic motor[C]//9th International Symposium on Advanced Topics in Electrical Engineering，Bucharest，Romania，2015：609-613.

[18]Lin Shuyu.Study on the radial composite piezoelectric ceramic transducer in radial vibration[J].Ultrasonics，2007，46(1)：51-59.

[19]Lin Shuyu.Study on the radial vibration of a new type of composite piezoelectric transducer[J].Journal of Sound and Vibration，2007，306(1-2)：192-202.

[20]王矜奉，蘇文斌，王春明，等.壓電振動(dòng)理論與應(yīng)用[M].北京：科學(xué)出版社，2011：81-122.

(編輯 于玲玲)

Stator Vibration Model of a Radial Energy Conversion Ultrasonic Motor

JiangChunrong1DongXiaoxiao2ZhangJinyang1JinLong2

(1.School of Electric Power Engineering Nanjing Institute of Technology Nanjing 211167 China 2.School of Electrical Engineering Southeast University Nanjing 210096 China)

A radial energy conversion ultrasonic motor with elastic blades is proposed in this paper.The structure and the operational principle of the motor are presented.The analytical model for the free and the forced radial vibration of the stator is investigated.Meanwhile，in order to carry out the contrast verification，the finite element model of the stator is developed as well as the modal and the harmonic analysis are conducted.The first order resonant frequency of the stator vibration in radial direction and the forced radial vibration amplitude stimulated by the applied voltage are obtained based on the two proposed models，and good agreements between the results obtained from the two models are observed.The first order resonant frequency of the stator radial vibration is measured with impedance analyzer，and the forced radial vibration amplitudes of the stator surface points stimulated by the applied voltage are measured with laser Doppler velocimeter.The experimental results are compared with the theoretical results and good agreements are obtained，which verifies the proposed analytical model and the finite element model for the stator vibration.Finally，a prototype machine is manufactured to verify the operational principle of the proposed radial energy conversion ultrasonic motor.

Ultrasonic motor，radial energy conversion，stator vibration，analytical model，finite element model

國(guó)家自然科學(xué)基金(51507076)、江蘇省自然科學(xué)基金(BK20140766)和江蘇省配電網(wǎng)智能技術(shù)與裝備協(xié)同創(chuàng)新中心開(kāi)放基金(XTCX201610)資助項(xiàng)目。

2016-02-18 改稿日期2016-04-11

TM35

蔣春容 女，1983年生，博士，講師，研究方向?yàn)槌暡姍C(jī)建模及控制。

E-mail： jj549307089@163.com(通信作者)

董曉霄 女，1990年生，博士研究生，研究方向?yàn)槌暡姍C(jī)理論模型、大功率壓電材料。

E-mail：dongxiaoxiao120@163.com