新型橡膠隔震支座臨界行為理論模型研究

孫新陽， 楊維國， 王 萌

(北京交通大學 土木建筑工程學院，北京 100044)

新型橡膠隔震支座臨界行為理論模型研究

孫新陽， 楊維國， 王 萌

(北京交通大學 土木建筑工程學院，北京 100044)

橡膠隔震支座在地震作用下同時受到巨大軸力與剪切變形，易發生穩定性問題進入臨界狀態，現行設計方法及計算理論不能準確計算臨界力及臨界位移，嚴重威脅隔震結構安全。提出計算橡膠支座臨界行為新型理論模型，根據支座進入臨界狀態時受力規律，以兩層豎向彈簧模擬支座轉動性能，非線性水平彈簧模擬剪切性能，建立力學模型對支座臨界行為進行分析。通過與試驗結果進行對比，表明建立的理論模型能夠準確模擬橡膠支座的臨界行為，解決了現存分析模型中需要依靠試驗校正系數以及誤差過大的問題，為隔震結構設計提供有力工具。

橡膠支座；水平剛度；穩定性；臨界力；力學模型；有限元分析

結構隔震技術是一種發展較快的結構震動控制技術，近年來已在高層及超高層建筑中得到廣泛應用[1-2]。橡膠隔震支座作為隔震體系中重要的隔震構件，不僅能夠提供較大的豎向剛度[3]，并且在地震作用下，橡膠層產生剪切變形，有效延長結構的水平周期，從而減小結構的慣性力[4]。

當結構遭遇罕遇地震時，支座在上部結構重力及地震傾覆力矩作用下，受到巨大壓縮荷載；同時，支座橡膠層產生較大剪應變，頂部剪切變形往往超過支座直徑。隨著剪應變不斷增加，支座水平剛度逐漸退化，當水平剛度降為0時，支座發生失穩進入臨界狀態(如圖 1所示)。臨界行為是支座的一種重要受力特征，支座的穩定性是隔震結構設計及支座設計時需要考慮的重要環節[5]，準確的預測支座的臨界位移與臨界力對于揭示支座受力規律具有重要意義。

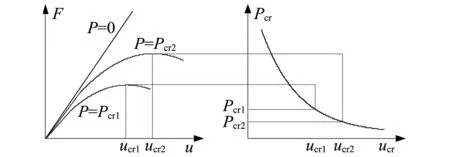
圖1 橡膠支座臨界行為Fig.1 Critical behavior of rubber bearings

因此，為了能夠模擬支座臨界行為下受力狀態，一些學者進行了廣泛研究，建立理論模型并推導了支座臨界力公式。Nagarajaiah等[6](1999)最早提出了能夠模擬支座臨界力的理論模型，該模型在雙彈簧模型(如圖 2所示)基礎上引入非線性，并通過臨界力試驗驗證了模型能夠有效模擬出臨界力隨位移增大而減小的特征，但模擬精度有所不足。Iizuka[7]同樣對雙彈簧模型進行改進，建立分析模型，較準確的模擬了豎向力與剪應變對剪力的影響，然而模型中非線性參數需經過試驗校正且對數值變化非常敏感[8]，增加了工程應用時的局限性。Han等[9](2014)總結上述模型并建立新型支座力學模型，模型很大程度上對模型進行了簡化，且提高了模型分析結果的準確性，但與支座進入臨界狀態時對角受拉受力狀態不符，理論性不足。以上研究對于推進支座精確理論模型發展及揭示支座受力規律具有重要意義。

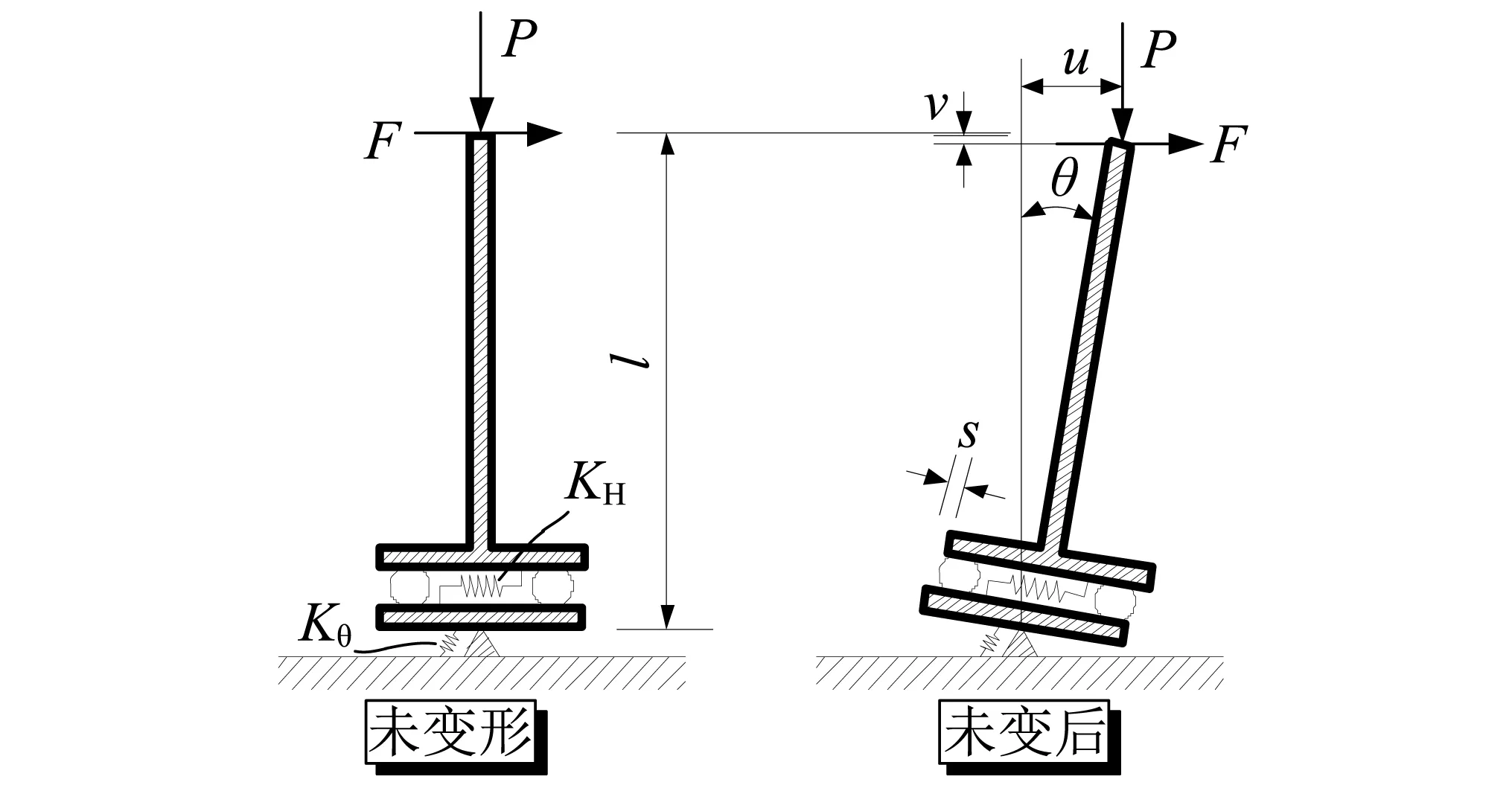
圖2 雙彈簧模型Fig.2 Two-spring model

為了研究疊層橡膠支座在臨界狀態下的受力規律，提出能夠準確模擬支座臨界行為的理論模型，解決現存理論模型中需要依靠試驗校正系數以及誤差過大的問題：本文首先根據現行臨界力計算方法，確定了基于有效面積模型的支座臨界力公式；然后從支座進入臨界狀態時受力機理入手，采用ABAQUS軟件建立支座非線性數值模型，通過對國外典型壓縮、剪切及臨界狀態試驗模擬，驗證了模型的精確性和實用性，從而指導理論模型建立；在此基礎上，綜合現有學者理論模型，建立了能夠有效模擬支座臨界狀態下受力規律的力學分析模型，并與試驗進行驗證，為支座受力進一步分析及工程應用奠定有力基礎。

1 支座臨界狀態理論

目前對于橡膠支座臨界力的計算方法，多基于小變形及橡膠線性假定，根據Haringx理論算得[10]，當支座頂部無剪切變形時，可以得到支座臨界力為

(1)

式中：Pcro為支座初始臨界力；GAs為支座剪切剛度，其中As=Abl/Tr，Ab為橡膠剪切面積，Tr為橡膠層總厚度；PE為歐拉荷載，PE=π2EIs/l2。

由于橡膠支座中PE≥GAs，式(1)簡化為式(2)的形式

(2)

地震荷載作用下，隔震層上部與基礎間發生相對位移，支座剪切變形增加，臨界力不斷減小。目前國內外采用的設計方法及規范中多根據圖3所示的有效面積模型計算，規定當頂部剪切位移為ucr時，臨界壓力Pcr為

(3)

式中：Ae為橡膠支座發生剪切變形時重疊區域面積；A為無剪切變形時橡膠層截面積。

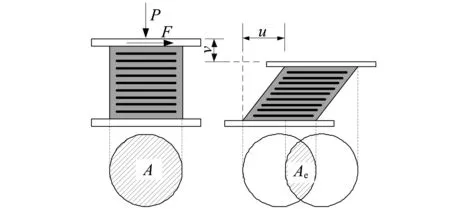
圖3 橡膠支座有效面積模型Fig.3 Effective area model of rubber bearing

由式(3)可以看出，支座臨界力隨著剪切位移增加而減小，式(3)中，當變形Ae=0時，臨界力減為0。

2 有限元模型驗證

隨著剪切變形增加，橡膠支座水平剛度不斷退化，在進入臨界狀態時出現零剛度現象，表現出強烈的非線性，支座應力狀態復雜。普通的有限元方法難以有效地模擬支座的臨界受力行為，需要建立能夠準確模擬橡膠支座壓縮、剪切以及大震作用下進入臨界狀態的有限元模型，為建立理論模型提供必要條件，同時為進一步分析提供有力工具。

為驗證所建立的有限元模型能夠準確模擬橡膠支座的實際受力情況，選取國外典型試驗進行驗證，選取文獻[11] (支座A0)中Test 8及Test 26驗證支座壓縮及剪切工況，同時選取文獻[12] (支座A0)及文獻[13](支座A1)驗證支座的臨界行為。試驗中支座參數，如表1所示。

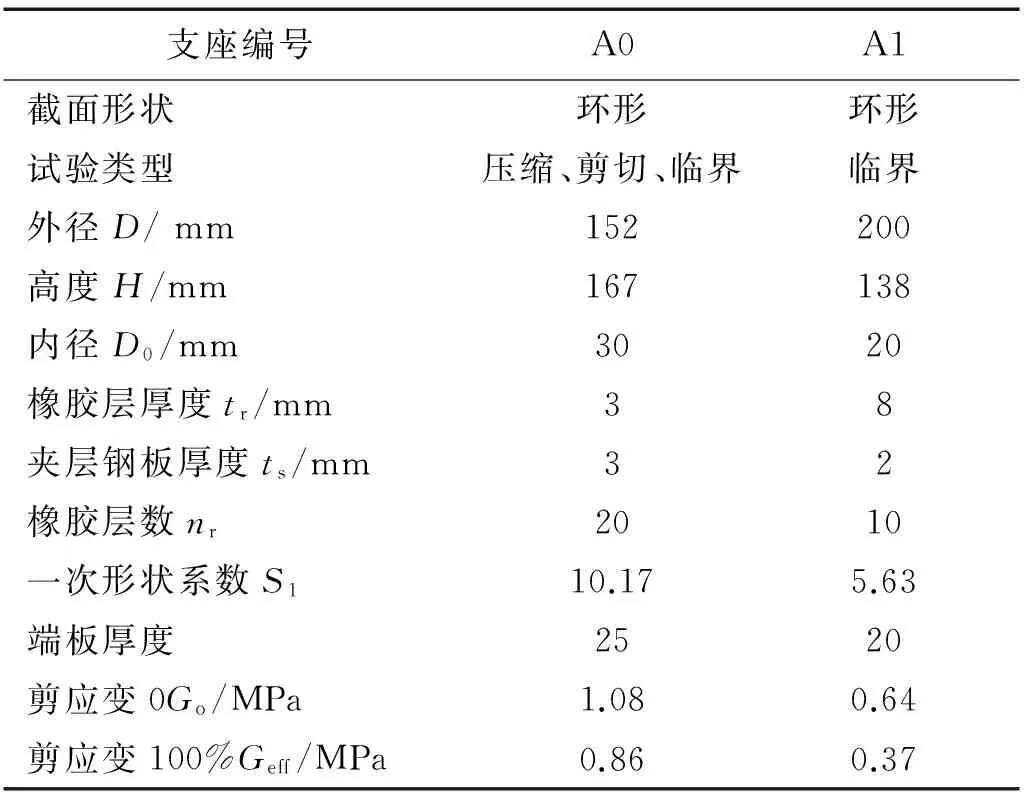
表1 橡膠隔震支座參數

2.1 有限元模型建立

采用ABAQUS軟件建立有限元模型，如圖 4所示，以雜交實體單元C3D8H模擬橡膠層，避免采用普通實體單元模擬橡膠材料產生體積自鎖，以單層非協調實體單元C3D8I模擬夾層鋼板及端板，避免完全積分時一階單元產生剪切自鎖[14]。夾層鋼板及橡膠層之間采用共用節點進行連接，避免采用接觸或耦合表面造成模型收斂困難與計算誤差。

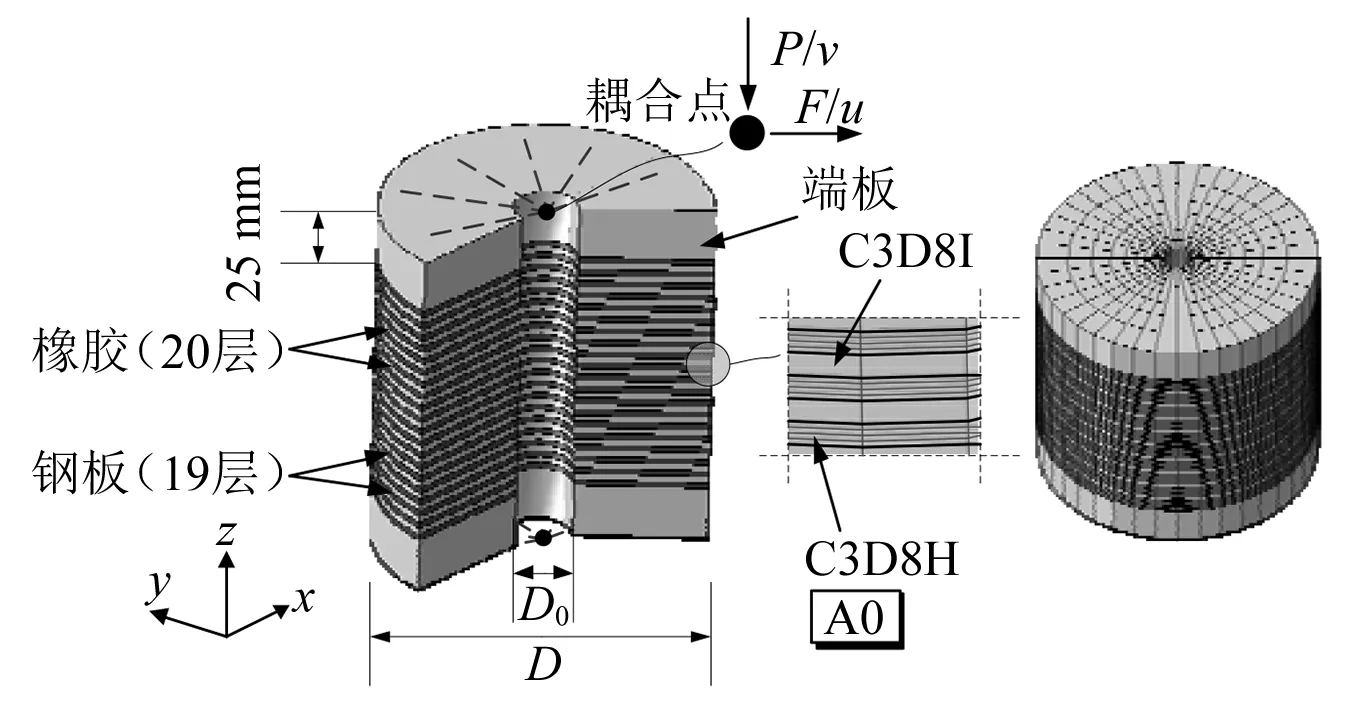
圖4 支座有限元模型Fig.4 Finite element model of bearings

為保持有限元邊界條件與試驗一致，同時為方便加載，分別在模型上下端面形心建立參考點，并將該表面自由度與參考點進行耦合。考慮實際試驗工況定義模型邊界條件，約束模型頂部參考點x向平動及轉動自由度，并固結下部參考點。有限元的加載過程與試驗一致：首先在頂部參考點施加z向荷載，模擬上部結構自重；考慮水平加載過程中支座剪切剛度不斷退化，因此以位移方式進行水平加載，通過施加y向位移，模擬隔震層在地震作用下產生的剪切變形。

2.2 本構模型選取與網格劃分

支座模型中鋼結構部分采用線彈性模型，材料彈性模量為200 Gpa，泊松比為0.3。由于橡膠材料是各向同性不可壓縮的超彈性體，故選取有限元軟件中用于模擬此類材料的超彈性本構模型，以應變勢能(U)來表示橡膠材料的力學性質。選取能夠較好的模擬橡膠材料在壓縮及剪切狀態下的受力特征Neo-Hookean本構模型進行模擬[15]，若已知橡膠剪切模量G與體積模量K，則Neo-Hookean本構模型應變勢能表達式為

(4)

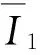
由于橡膠材料不可壓縮(泊松比ν=0.5)，體積在荷載作用下保持不變，在軸力與剪力共同作用下，橡膠材料產生較大變形，網格易產生畸變影響計算結果，因此需要對模型網格尺寸進行敏感性分析，確定合適的網格尺寸。

在對支座進行網格劃分時，為了保證單元在平面內長寬比近似為1，避免單元形狀影響計算結果，徑向單元尺寸根據式(5)進行劃分。

(5)

式中：b為徑向連續兩個單元長度比；Nr為徑向單元數；D0與D分別為支座內外半徑。得到當有限元模型周向劃分40份、徑向10份、厚度方向劃分4份可使計算誤差在2%以下，支座模型的尺寸示意如圖 4所示。

2.3 有限元與試驗計算結果對比

支座A0有限元計算的荷載—位移曲線與壓縮、剪切試驗曲線對比如圖 5所示，數值模擬結果與試驗結果基本一致，數值模型能夠較為準確地模擬出橡膠支座的壓縮及剪切特性。加載結束時，圖 5中支座剛度計算值與試驗值相差在5%以內，說明所建立的有限元方法能夠準確模擬橡膠支座壓縮與剪切剛度。

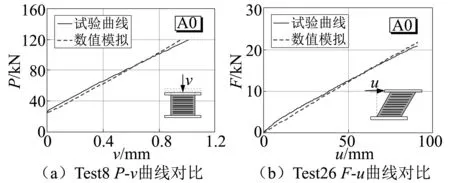
圖5 支座A0壓縮及剪切試驗有限元與試驗結果對比Fig.5 Comparison of rubber A0 between FE model and test results

不同預壓力P作用下，支座A0剪力-位移曲線數值模擬與試驗結果對比如圖6所示，數值模擬結果與試驗曲線吻合良好，有限元方法能夠有效模擬出支座在軸力與剪力共同作用下進入臨界狀態，并能夠較準確地預測出支座到達臨界狀態時的水平剪力與臨界位移。圖7為支座A0與A1臨界位移-臨界荷載曲線，可以看出，隨著頂部荷載增加，支座臨界位移減小，有限元模型同樣可以模擬出此現象。

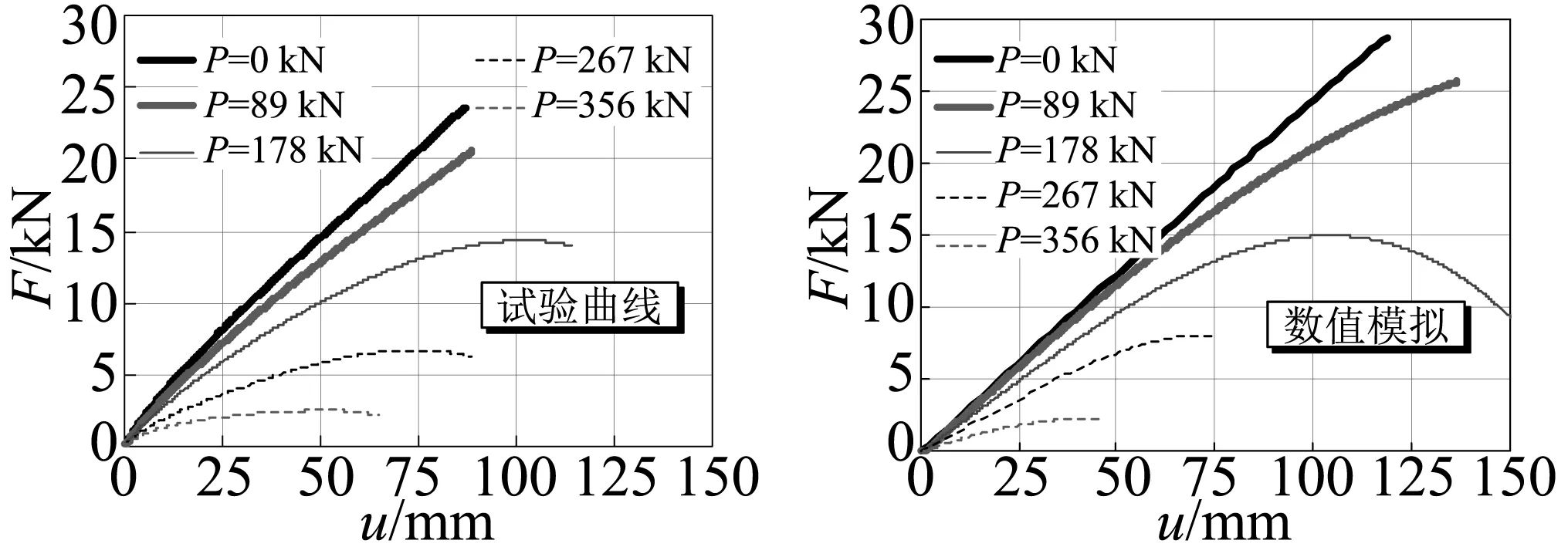
圖6 支座A0臨界狀態試驗有限元與試驗結果對比Fig.6 Comparison of rubber A0 between FE model and test results

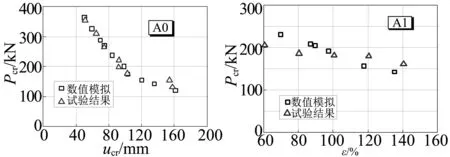
圖7 支座A0與A1臨界狀態試驗有限元與試驗結果對比Fig.7 Comparison of rubber A0 and A1 between FE model and critical test results

國際標準《建筑隔震支座》[17]及我國規范《橡膠支座》[18]對天然橡膠支座內部橡膠材料拉伸性能做了限值規定，要求其拉伸強度≥12 MPa。《建筑抗震設計規范》[19]規定：隔震支座在大震作用下的最大水平位移應滿足下列要求

umax≤0.55D

(6)

umax≤3Tr

(7)

式中：umax為隔震支座最大水平位移；D為支座直徑。圖 8為A0支座頂部壓力為10 MPa且位移達到臨界位移(u=103 mm)時豎向S33應力，圖中正值為受拉，負值受壓。可以看出，當支座進入臨界狀態時，即使頂部受到壓力作用，支座右上及左下角仍出現出拉應力區，拉應力大小約為8.5 MPa，剪切位移達到規范限值u=0.55D(83.6 mm)時，角部拉應力為6.7 MPa，均未達到橡膠極限抗拉強度，但拉應力明顯。支座拉應力區的出現是支座臨界狀態的一大受力特征，確定拉應力大小可有效指導理論模型的建立及進一步分析。

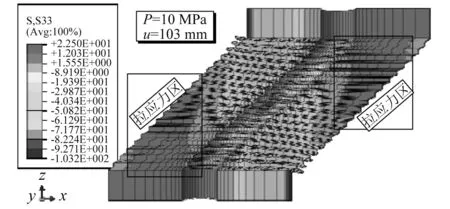
圖8 P=10 MPa, u=103 mm時A0支座豎向應力云圖Fig.8 Bearing A0 vertical stress contour for P=10 MPa at u=103 mm

3 橡膠支座力學模型

3.1 模型描述

根據以上橡膠支座的受力特征，建立如圖 9所示的力學模型。模型包含一根剛性柱、一個剪切彈簧及上下兩組豎向彈簧組成，其中剛性柱長為l，剪切彈簧剛度為Ks，豎向彈簧本構模型定義為雙線性：壓縮向及拉伸屈服前剛度為Ec，屈服后進入塑性。

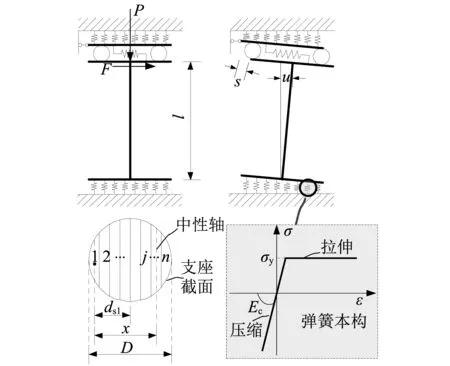
圖9 橡膠支座力學模型Fig.9 Mechanical model of rubber bearings

剛性柱頂部在軸力P與剪力F的作用下，支座產生轉角為θ，剪切彈簧變形為s，柱頂端水平位移為u，頂部在彎剪變形共同作用下豎向位移為v，則柱頂位移u及v可由s及θ表示為

u=scos(θ)+lsin(θ)

(8)

v=ssin(θ)+l[1-cos(θ)]

(9)

考慮模型在變形狀態下受力平衡，則有

Qs=Fcos(θ)+Psin(θ)

(10)

Ms=Pu+F(l-v)

(11)

式中：Qs為剪切彈簧變形為s時內力，Ms為剛性柱底部所受外力彎矩。采用文獻[7]中逐步增量法對式(8)～式(11)進行求解，根據文獻[6]研究，剪切彈簧受力關系為

(12)

式中：Go為橡膠初始剪切模量；Tr為支座中橡膠層總厚度；Ab為橡膠剪切面積；Cs為無量綱常數。文獻[20]對不同支座進行研究，得出兩支座Cs分別為0.282 1及0.325時模擬結果較好，為方便計算，本模型中取Cs=0.3模擬剪切彈簧中非線性關系。

兩排豎向彈簧內力由外力計算得到，根據受力平衡條件有

(13)

(14)

式中：σsj為模型中剪切彈簧變形為s時下部第j根彈簧中應力，Aj為第j根彈簧截面積，dsj為第j根彈簧截面中心與支座截面中心距離，豎向彈簧變形關系為

(15)

式中：x為中性軸與第1根彈簧中心距離；εsj為第j根彈簧應變；ls為彈簧未發生變形時長度。

為保證理論模型中初始轉動剛度與原支座相同，豎向彈簧長度ls需滿足

(16)

式中：Ec為橡膠材料壓縮模量；E為支座抗彎模量，有E=Ec/3；I為支座截面慣性矩；Tr為橡膠層總厚度，不同截面形狀支座壓縮模量根據橡膠初始剪切模量與一次形狀系數計算得到[21]。

豎向彈簧本構關系如式(17)所示，根據支座進入臨界狀態時支座角部受拉區拉應力值確定理論模型中模型中屈服強度，得到σy=8Go時能準確反映支座受力關系。

(17)

3.2 模型參數確定

理論上當模型上下兩側豎向彈簧足夠多時，模型可模擬支座實際受力狀態，但豎向彈簧過多，會增加模型的復雜程度與計算時間，故選取A0支座進行模型彈簧數量n參數研究，確定能夠準確模擬支座臨界行為的最小彈簧參數，同時為了減小由于支座失穩而使支座到達臨界狀態至剪力為0區段產生震蕩，對此區間曲線進行光滑化。

模型取不同豎向彈簧數量時支座剪力—位移曲線如圖 10所示，由圖 10可知，彈簧數目增加，剪切位移相同時水平剪力減小，臨界位移減小。以上下兩側分別有20根彈簧計算結果近似為精確解，考察模型中彈簧數量對于分析結果的影響，計算各不同彈簧數各加載工況下水平剪力與臨界位移平均誤差(如表2所示)。可知當n取10時，可保證當支座到達臨界狀態時，水平剪力與臨界位移誤差小于2%。因此，后續分析中取n=10進行模擬。

圖10 不同豎向彈簧數量時A0支座F-u曲線Fig.10 Shear force-lateral displacement results of bearing A0 for different vertical springs number

彈簧數目誤差/%213.563.8101.3200

3.3 模型驗證

根據上述模型，支座A0的剪力-位移曲線與試驗曲線對比如圖11所示，由圖可知，所建立的理論模型能夠較準確的模擬出支座水平剛度隨變形增大而減小的特性，力學模型曲線與試驗曲線吻合較好。由于理論模型中剪切彈簧非線性受力關系假定對實際支座剪切性能的簡化，使得當剪切變形較大(u>0.5D)時，理論模型曲線與試驗曲線沒有完全重合；同時，由于模型中豎向彈簧本構模型屈服后部分對于支座轉動性能的簡化，使支座頂部壓力較大(P>10 MPa)時，支座進入臨界狀態后水平剛度與試驗值產生一定誤差。

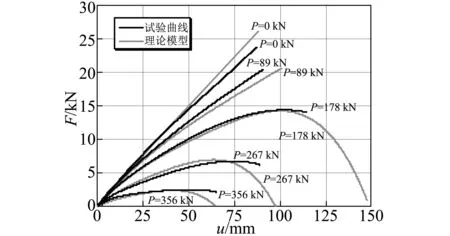
圖11 支座A0 F-u曲線理論模型與試驗結果對比Fig.11 Comparison of F-u for rubber A0 between mechanical model and test results

支座A1與A2臨界力與臨界位移分析結果與試驗結果對比如圖 12所示，理論模型結果與試驗結果吻合較好，隨著臨界力增加，支座臨界位移減小。我國《建筑抗震設計規范》規定：直徑小于300的橡膠隔震支座最大壓應力設計值不宜大于10 MPa。當支座頂部壓力大于10 MPa時，理論模型仍然能夠較準確的反映臨界力與臨界位移關系，與試驗相比，最大誤差均控制在20%以內，所建立的理論模型能夠準確分析支座在軸力與剪力組合作用下進入臨界狀態。現行計算方法(圖中曲線)雖能反映臨界力-臨界位移變化趨勢，但在相同臨界位移下，過于低估臨界力大小，不能準確預測支座臨界特性。

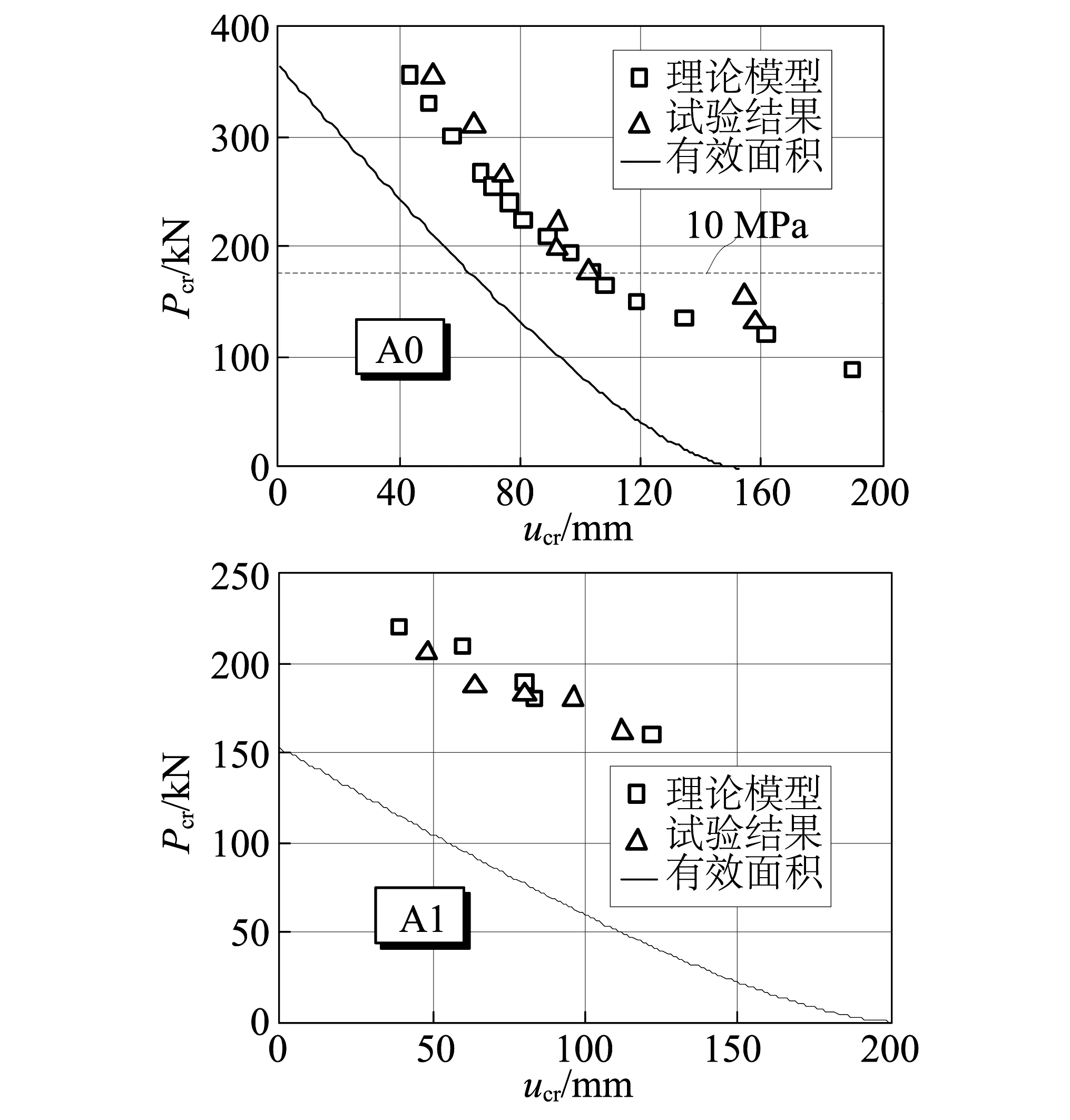
圖12 臨界力-臨界位移曲線理論模型與試驗結果對比Fig.12 Comparison of critical load-lateral displacement between mechanical model and test results

4 結 論

為了模擬橡膠隔震支座在軸力與剪力組合作用下的臨界行為，本文建立能夠準確模擬支座臨界力與臨界位移大小的支座理論模型。模型以非線性水平彈簧模擬剪切性能，以兩排豎向彈簧模擬轉動性能。結合國外典型臨界試驗，驗證了所提出的力學模型的準確性和有效性，并與現行設計中臨界狀態計算方法進行對比，得到以下結論：

(1) 隨著剪應變增加，支座臨界壓力減小；隨著頂部壓力與剪切位移增加，支座水平剛度不斷退化，并在臨界位移處出現零剛度現象。所建立的理論模型能夠準確的模擬出此現象。

(2) 與現有學者所提出的模型相比，本文建立的理論模型中，所有參數均不需試驗校正，并與實際支座進入臨界狀態時對角受拉受力特征相符，為工程設計了提供便利條件。

(3) 現行支座臨界力計算設計方法過于保守，嚴重低估了支座的臨界力。小震(ε<100%)作用下，臨界力試驗值約為計算值1.5倍，大震(ε>150%)作用下，試驗值約為計算值3倍。

[1] 周錫元, 閻維明, 楊潤林, 等. 建筑結構的隔震、減振和振動控制[J].建筑結構學報,2002,23(2):2-12. ZHOU Xiyuan, YAN Weiming, YANG Runlin, et al. Seismic base isolation, energy dissipation and vibration control of building structures[J]. Journal of Building Structures,2002,23(2):2-12.

[2] 杜東升, 王曙光, 劉偉慶, 等.高層建筑組合隔震的設計方法及應用[J].東南大學學報(自然科學版),2010,40(5):1039-1046. DU Dongsheng, WANG Shuguang, LIU Weiqing, et al. Design method and its application in hybrid base-isolation of high-rise buildings[J]. Journal of Southeast University (Natural Science Edition), 2010, 40(5): 1039-1046.

[3] WARN G P, WHITTAKER A S, CONSTANTINOU M C. Vertical stiffness of elastomeric and lead-rubber seismic isolation bearings[J]. Journal of Structural Engineering, 2007, 133(9): 1227-1236.

[4] WEISMAN J, WARN G P. Stability of elastomeric and lead-rubber seismic isolation bearings[J]. Journal of Structural Engineering, 2011, 138(2): 215-223.

[5] WARN G P, WEISMAN J. Finite-element and experimental investigation of the post-buckling stability of an elastomeric seismic isolation bearing[C]∥Structures Congress 2010. Orlando, FL: ASCE, 2010: 1452-1461.

[6] NAGARAJAIAH S, FERRELL K. Stability of elastomeric seismic isolation bearings[J]. Journal of Structural Engineering, 1999, 125(9): 946-954.

[7] IIZUKA M. A macroscopic model for predicting large-deformation behaviors of laminated rubber bearings[J]. Engineering Structures, 2000, 22(4): 323-334.

[8] HAN X, KELLEHER C A, WARN G P, et al. Identification of the controlling mechanism for predicting critical loads in elastomeric bearings[J]. Journal of Structural Engineering, 2013, 139(12): 04013016.

[9] HAN X, WARN G P. Mechanistic model for simulating critical behavior in elastomeric bearings[J]. Journal of Structural Engineering, 2014, 141(5): 04014140.

[10] HARINGX J A. On highly compressive helical springs and rubber rods and their applications to free mountings—Parts I, II and TTT[J]. Philips Research Reports, 1948,3(6):401-449.

[11] WARN G P. The coupled horizontal-vertical response of elastomeric and lead-rubber seismic isolation bearings[D]. New York: The State University of New York, 2006.

[12] SANCHEZ J, MASROOR A, MOSQUEDA G, et al. Static and dynamic stability of elastomeric bearings for seismic protection of structures[J]. Journal of Structural Engineering, 2013,139(7):1149-1159.

[13] CARDONE D, PERRONE G. Critical load of slender elastomeric seismic isolators: an experimental perspective[J]. Engineering Structures, 2012, 40: 198-204.

[14] ABAQUS. Analysis user’s manual I_V. Version 6.10 [M]. USA: ABAQUS, Inc., Dassault Systèmes, 2010.

[15] 孫新陽, 楊維國, 王萌, 等. 剪切變形下橡膠支座壓縮剛度比分析研究[J]. 工程力學, 2017,34(1):58-68. SUN Xinyang, YANG Weiguo, WANG Meng, et al. Compression stiffness ratio of rubber bearings under shear deformation[J]. Engineering Mechanics, 2017,34(1):58-68.

[16] WARN G P, WHITTAKER A S. A study of the coupled horizontal-vertical behavior of elastomeric and lead-rubber seismic isolation bearings[R]. Multidisciplinary Center for Earthquake Engineering Research, 2006.

[17] International Standard: Elastomeric seismic-protection isolators. Part 3: Applications for buildings. Specifications: ISO 22762-2[S]. 2010.

[18] 橡膠支座第3部分: 建筑隔震橡膠支座:GB 20688.3—2006[S]. 北京: 中國建筑工業出版社,2006.

[19] 中華人民共和國建設部. 建筑抗震設計規范:GB 50011—2010 [S]. 北京. 中國建筑工業出版社, 2010.

[20] VEMURU V S M, NAGARAJAIAH S, MASROOR A, et al. Dynamic lateral stability of elastomeric seismic isolation bearings[J]. Journal of Structural Engineering, 2014, 140(8): A4014014.

[21] CONSTANTINOU M C, KARTOUM A, KELLY J M. Analysis of compression of hollow circular elastomeric bearings[J]. Engineering Structures, 1992, 14(2): 103-111.

New theoretical model of rubber bearings for simulating critical behavior

SUN Xinyang, YANG Weiguo, WANG Meng

(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Rubber seismic isolation bearings are usually subjected to large axial loads and lateral displacements at the same time during earthquakes, and they are prone to turn into critical state. The current design methods and calculation approaches cannot calculate the critical forces and corresponding displacements with enough accuracy, which poses a direct threat to the isolated structures. Therefore, a new theoretical model that could simulate the critical behaviors of rubber bearings was proposed. According to the mechanics regularity of bearings in critical state, the rotational behavior of rubber was represented by two groups of vertical springs, the shear behavior was modeled by a nonlinear horizontal spring, and then a mechanical model was established to analyze the critical behaviors of rubber bearings. By comparing with test curves, the results show that the model has the ability to simulate the critical behaviors of rubber bearings with ideal accuracy. It can tackle the problems of the necessity of relying on experimentally calibrated parameters and the appearance of considerable errors by existing models, and it is able to provide a powerful tool for isolated structures design.

rubber bearing; horizontal stiffness; stability; critical load; mechanical model; finite element analysis

國家自然科學基金資助項目(51578046;51408031)

2016-02-14 修改稿收到日期： 2016-04-11

孫新陽 男，博士生，1990年生

楊維國 男，博士，教授，博士生導師，1973年生

E-mail：wg_yang@263.net

TU352.1

A

10.13465/j.cnki.jvs.2017.10.002