基于Holt—Winters時間序列的圖書選題預測模型

林海++康寶中

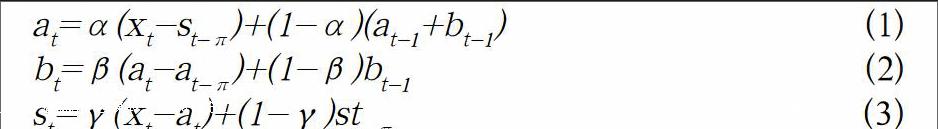
摘要：針對出版選題策劃依賴主觀經驗的問題，提出了采用Holt-Winters時間序列預測模型按圖書類別預測圖書銷量的方法。為出版單位作出合理的選題策劃提供依據。通過選題預測可有效把握市場規律，迎合用戶消費傾向，有效減少因錯過最佳銷售時機造成庫存積壓導致人力物力的消耗。

關鍵詞：圖書銷售預測；數據挖掘；R語言；圖書選題

中圖分類號：TM73 文獻標識碼：A 文章編號：1007-9416（2017）03-0051-03

圖書選題作為圖書出版的最初環節，歷來被出版單位所重視。本文主要解決出版單位確定某一時間出版選題類別的問題。如提供未來幾個月內，某些類別的圖書將會有較好的收益。出版行業選題策劃的基本流程包括信息篩選、選題設計、選題論證、選題優化等[1]，圖書銷售數據直觀反應市場規律與用戶消費傾向，對選題策劃有著至關重要的影響。近年來隨著圖書銷售數據管理的規范化、信息化，選題策劃人員面對書城近期銷售排行榜，銷售月報以及《開卷圖書調查報告》等眾多報表，進行深度研究、定量分析，獲得的結果極有價值，是未來圖書市場調查研究的趨勢。[2]

鑒于圖書市場具有短期的波動性與中長期的周期性、銷售數量巨大與銷售品種的繁多同時并存的特點，給出版機構進行選題策劃帶來很大的困難。根據圖書市場中長期周期性特點，提出了使用時間序列方法預測圖書銷量，可為出版單位推薦選題類別和選題規劃的最佳時段。

1 基于Holt-Winters模型的銷售預測分析

1.1 預測模型應用

Holt-Winters模型是較常見的預測模型，由Winters（1960）提出的，又由后人不斷改進（如Hyndman et al.（2002），Cipra and Romera（1997），Cipra et al.（1995）），才有了現在的形式[3]。Holt指數平滑法加入了趨勢指數作為修正而建立的模型，無論用在什么領域，Holt指數平滑法都被有效的驗證，并且具有優秀的預測能力（Holt，2004；Eddie & Everette，2010；Luis，2011）[4]。Holt-Winters模型通常分加法模型和乘法模型，分別適用于季節變動大致相等和長期趨勢大致成正比的情形。

時間序列預測方法在眾多預測領域得到了應用廣泛，文獻通過運用時間序列對黃河徑流量等水文數據預測，為黃河防汛作出預，進而減弱自然災害的影響；文獻[6]同樣采用時間序列方法對自動售貨機的銷量進行預測分析，可提出一個快速的銷售方案，減少人力物力不必要的耗費。

通過大量論文例證表明時間序列預測方法不僅廣泛應用于各預測領域，而且適用于銷售數據的預測分析，鑒于圖書銷售市場具有一般普遍性，故本文選用的時間序列方法對圖書銷售數據進行預測是切實可行的。

1.2 Holt-Winters三參數指數平滑方法原理

指數平滑法是移動平均法的改進和發展，Holt-Winters三參數指數平滑模型本質上是一種高級指數平滑模型，可同時處理趨勢和季節性變化，可適當地過濾隨機波動的影響，對兼有長期趨勢和季節模式的數據進行預測。

當時間序列圖顯示的時間序列的季節變動大致相等時，采用加法模型；當時間序列的長期趨勢大致成正比時，應該采用乘法模型。鑒于本文討論的數據規律與加法模型相符合，故本文選擇季節和趨勢為加法模型，假設要進行指數平滑的序列為{xt}，則Holt-Winters三參數指數平滑模型構造如下：

at=α（xt-st-π）+（1-α）（at-1+bt-1） （1）

bt=β（at-at-π）+（1-β）bt-1 （2）

st=γ（xt-at）+（1-γ）st-π （3）

其中：π為季節性時間的長度π=12，對于月度數據；s季節調整因素；xt為現行數值；at為平滑值；bt為長期趨勢值；γ為加權值；α，β為調整因子；t為當前時間。（1）式中xt為圖書銷售數據的序列值，經過參數α的平滑處理得到平滑序列at，同理長期趨勢序列bt與周期序列st經過參數β與γ的處理后得到。

預測值由下式計算：

y= at+ kbt+ st+k-π

其中k表示向后平滑期數，即決定預測未來幾個月份的序列的參數，y值即所預測圖書銷量序列。

1.3 數據清洗

以《開卷圖書銷售報告》（2013-2016）為例，該數據覆蓋全國2000余家實體書店門市，20余家獨立網店及天貓書城，具有良好的連續性、代表性和完整性。采用2012-2013連續2年的圖書零售市場逐月觀測數據作為訓練集，2014-2015年為測試集，銷售總碼洋31.77億元、銷售圖書總計2300余萬本。

首先對原始銷售數據進行數據清洗，剔除冗余字段、缺失字段后，保留規范化和有效的數據，如銷售分類、銷售量、售價、時間等字段；然后按年份與銷售分類分組統計。篩選后對各圖書銷售分類數據分析，包括銷售類別、碼洋與市場占有率。

鑒于每本圖書作品在圖書出版過程中都要進行ISBN號申請，申請目的主要是為了圖書市場更好的管理與規范，確保出版發行高質量圖書。申請時長作為一個重要因素影響出版單位出版選題的規劃，ISBN的平均申領時長是一個需要獲取的重要指標。

1.4 確定預測模型

圖書銷量的訓練和預測過程大致如下所示，首先在（1）式之前將數據dataframe1準備就緒，通過（2）式建立預測模型，將測試集帶入預測模型由plot函數比對擬合程度后，確定參數后即可由（3）式預測圖書銷量。

s1=ts（dataframe1，frequency=12， start=c（2012，1）） （1）

bookforecasts <- HoltWinters（s1，alpha=TRUE，beta=0， gamma=0.1） （2）

forecasts <- forecast.HoltWinters（bookforecasts， h=4）（3）

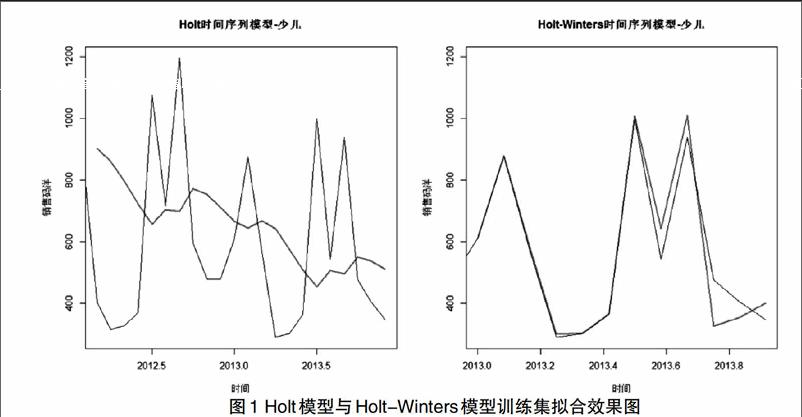
采取對少兒類圖書舉例分析，其它類別圖書分析方法類似，在此不再贅述。首先通過對Holt模型與Holt-Winters模型進行對比分析，如圖1所示橫軸表示年份，縱軸表示銷售碼洋，圖中黑色曲線表示實際圖書銷售碼洋變化規律，粗體曲線為模型對訓練集的擬合效果。

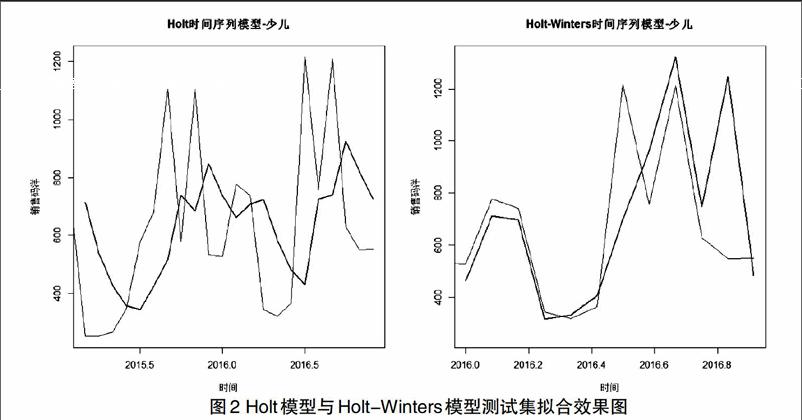
根據訓練集選取的時間序列預測模型，對測試集做時間序列預測。對比效果如圖2所示，橫軸表示年份，縱軸表示銷售碼洋，圖中黑色曲線表示實際圖書銷售碼洋變化規律，粗體曲線為模型對測試集的擬合效果。由圖2可表明Holt-Winters模型擬合效果優于Holt模型，所以選取Holt-Winters模型進行銷量預測。

通常評估模型擬合程度與誤差分析，通過預測誤差殘差偏移做自相關和偏相關分析，可判定預測模型的統計學意義。然后對Holt-Winter時間序列模型預測結果的誤差殘差偏移做自相關ACF和偏相關PACF分析，如圖3所示，圖3中第一部分橫軸表示時間，縱軸表示誤差殘差偏移量，曲線描述了預測值與實際值波動范圍的差值。圖3中的第二部分和第三部分表示殘差自相關圖與殘差偏相關圖，ACF與PACF隨著階數的升高，殘差均在意義界限虛線之內，表示預測結果符合統計學意義。由此表明選定的預測模型符合預期要求。

2 實驗結果及應用

2.1 預測圖書銷量

因為時間序列預測隨受近期數據影響因子較大，預測時間較長會丟失預測精確度，所以選取預測模型預測未來四個月的各類別圖書銷量。預測結果如圖4所示，其中橫軸表示時間，縱軸表示銷售碼洋，黑色曲線為實際銷售碼洋的值，其中圓點表示2016年1月只4月的月銷售碼洋，深灰色區域表示85%的置信區間，灰色區域表示95%的置信區間。

預測得到的預測結果如表1所示，時間表示預測時間，為2016年1月至4月，預測結果為各月份的銷售碼洋數值。

同理可得其余類別圖書未來4個月的銷售預測和所占比例。

2.2 預測結果分析與應用

根據本文預測數據，可以通過用戶輸入一定范圍內的年月信息（輸入的年月信息跨度較大會有較大的誤差，造成推薦方案的不準確性），由表2中的數據可以為出版單位提供出版選題比例結果推薦方案；如輸入2016年1月后，可以推薦給用戶該月份的選題比例，如推薦可提供較多盈利的類別TOP 8（排名前8種類別），如法律、文學、傳記、政治經濟與管理、少兒以及這六種類別選題的推薦比例，出版單位用戶可以由此可獲得各類別選題的結構比例推薦方案。

另一方面，由出版單位提供選題基本信息，可根據分類圖書平均申領時間表為出版單位選題規劃日期給出精確到日的信息。如出版單位提供的選題類別、頁數、開本、裝訂形式、首印量等信息，可以根據類別得到選題的ISBN申領時長；因為不同頁數、開本、裝訂形式的圖書作品印刷周期不同，如頁數較多并且裝訂形式是精裝版的圖書耗費的印刷時間也比較長，所以根據頁數、開本、裝訂形式、首印量等信息可以估算出印刷時耗。由以上兩部分時長可較為準確的得到該類選題的時耗，出版單位便可根據選題耗費時長提前規劃相應類別選題。

通過以上分析，從數據層面提供了選題預測的可靠性，并且從數量給予出版單位用戶直觀的反應，為出版單位某一時間出版什么類別選題提供了依據。由此使用以上方法可以建立起一整套根據圖書銷售數據對圖書選題規劃的應用，為圖書出版行業建立大數據分析的奠定基礎。

3 結語

本文運用時間序列的方法，基于圖書銷售數據采用數據挖掘分析方法，預測出各銷售類別圖書的銷售碼洋，進而為出版單位提供未來一段時間內某一類選題的推薦方案，并針對選題規劃周期時長提供預測，為出版單位選題規劃周期提供精確到日的推薦方案，為實現出版單位收益最大化提供良好的保障。

參考文獻

[1]傅祚華.選題策劃與出版流程[J].中國編輯，2016.2.

[2]李長青.如何透視圖書銷售數據背后的奧秘——圖書銷售數據定量分析方法淺探[J].科技與出版，2008（03）.

[3]沙川.Holt-Winters時間序列模型參數估計和預測[D].南京大學，2011.

[4]廈瑞鴻，鄭博文.醫院衛材需求預測與存貨管理[J].國立云林科技大學全球運籌管理所碩士論文，2013.1.