基于免組裝有限元的懸架控制臂拓撲優化

卞翔+方宗德

摘 要：為了提高拓撲優化在實際工程應用中的速度，將一種基于拓撲靈敏度的拓撲優化算法與免組裝有限元法結合，對汽車懸架控制臂進行多工況拓撲優化.該方法使用一致的體素單元劃分網格，用壓縮共軛梯度法（DCG）加速有限元的求解，得到結構的應力和應變場，從而獲得拓撲靈敏度場，用來控制結構拓撲變化.通過添加多工況優化以及加工約束功能，使該方法更符合工程應用的要求.通過對比，該方法和商用軟件能夠獲得性能接近、形狀相似的優化結構，而整個優化過程的速度有顯著提高.

關鍵詞：懸架控制臂；多工況拓撲優化；免組裝有限元；體素化；壓縮共軛梯度法；拓撲靈敏度

中圖分類號：U463.33 文獻標志碼：A

Topology Optimization of Suspension Control Arm Based on Assembly-free Finite Element Method BIAN Xiang， FANG Zongde

（Department of Mechanical Engineering， Northwestern Polytechnic University， Xian 710072， China）

Abstract： A suspension control arm was optimized by topology optimization under multi-working condition. In order to improve the speed of topology optimization for practical engineering problems， a topology optimization method based on topological sensitivity was combined with an assembly-free finite element method. The structure was discretized via uniform voxels. A deflated conjugate gradient （DCG） method was used to accelerate the finite element analysis. After the finite element analysis， the stress and strain field can be used to generate the topological sensitivity field， and the topological sensitivity field can be used to control the change of topology. Multi-working condition optimization and manufacturing constraints were used to make the method more suitable for practical problem. The comparison shows that the method can result in the close performance and similar shape of optimized structure to the commercial software. Meanwhile， the speed of the entire optimization is increased significantly.

Key words：suspension control arm； topology optimization under multi-working condition； assembly-free finite element method； voxelization； deflated conjugate gradient； topological sensitivity

輕量化設計是汽車設計中的一項重要內容，對于降低重量、提高性能、降低油耗等有重要作用.拓撲優化技術在汽車結構的輕量化設計中運用越來越多，拓撲優化能在結構設計的初始階段提供一個概念性設計，使結構在布局上采用最優方案，改變了以往的設計、校核、修改這樣一個不斷反復的開發流程，可以提高設計效率和質量，縮短研發周期，降低成本.

近年來，拓撲優化技術逐漸成熟，國內外研究較多的有固體各向同性材料懲罰法（Solid Isotropic Material with Penalization，SIMP）[1]，進化結構優化法（Evolutionary Structural Optimization，ESO）[2-3]，水平集法（Level-Set）[4-5]等.其中SIMP方法基于有限元法，給每個單元賦予偽密度，通過優化各單元的偽密度來達到優化目標[6].由于其概念簡單，算法容易實現，被推廣應用于多材料、多工況、多物理場等多種實際問題中，成為主流的拓撲優化方法之一[7].目前，常用的商用拓撲優化軟件如 Hyperworks 和 ANSYS 都采用SIMP方法進行拓撲優化.國內有許多研究使用Hyperworks進行汽車零部件的拓撲優化設計，文獻[8-11]使用Hyperworks對轉向節、懸架控制臂、發動機懸置支架、車架等汽車結構進行了拓撲優化設計.

如今，拓撲優化技術發展的挑戰之一是計算速度[12]，尤其是對于大型有限元模型，比如對于上百萬自由度的優化問題需要數小時甚至數天來完成.文獻[12-14]提出了一種基于拓撲靈敏度的拓撲優化算法，對多目標優化問題帕雷托最優解的計算十分高效，該方法將拓撲靈敏度作為水平集，用來控制孔洞的形成，得到的結果相比于SIMP方法更加清晰、明確，不需要網格過濾等技術.但是這種方法的研究還處于初步階段，沒有商用軟件全面的功能，還不能滿足實際的工程應用.

本文基于C++語言，將這種基于拓撲靈敏度的拓撲優化算法與一種免組裝（Assembly-free）有限元分析方法[15-16]相結合，并用壓縮共軛梯度法[17]進一步加速拓撲優化的速度，通過添加多工況優化、加工約束等滿足實際工程應用的功能，用于汽車零部件的結構優化設計.以懸架控制臂的優化為例，通過與商用軟件Hyperworks對比，證明該方法的有效性.

1 免組裝有限元模型

1.1 懸架控制臂體素化模型

一些商用軟件需要花費大量時間在網格劃分上，需要人工進行簡化幾何、拆解幾何和改變網格尺寸等操作，才能獲得滿足軟件要求的網格模型.

體素化[18]是一種簡單的有限元網格離散方法，通過統一的六面體單元（體素）來劃分幾何模型.由于使用了形狀和尺寸一樣的單元，體素化網格具有穩健性和內存占用空間低的優點[19]，能夠配合免組裝方法，提高有限元分析的計算速度.

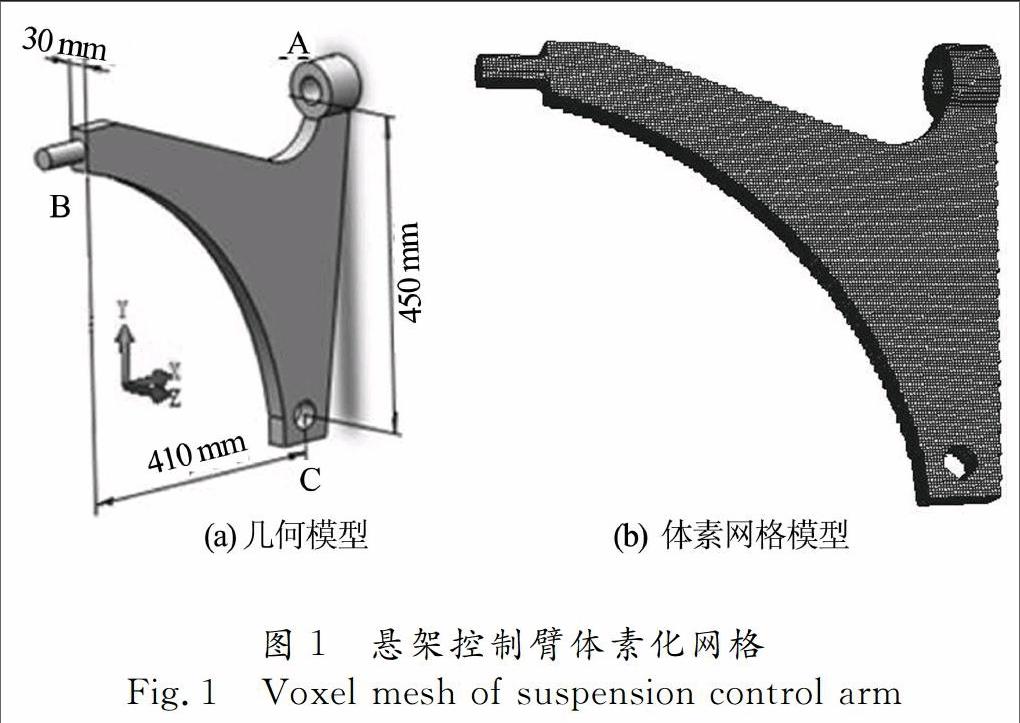
體素化模型由于使用一致的網格，可以通過編程實現快速的自動網格劃分，圖 1 （a）所示是懸架控制臂的幾何模型，圖1（b）為相應的體素網格模型，單元數量為79 000，自由度為280 000，自動網格劃分時間僅為4 s.

由于網格一致性的限制，體素化模型不能夠完全精確體現所有的幾何細節.但是考慮到拓撲優化是設計初期的概念設計階段，其主要目的是為后期設計提供參考，在多數情況下，尤其是對于諸如柔度、頻率等全局參數的優化變量，一些幾何細節并不重要.對于本文考慮的懸架控制臂模型，3個連接端這幾個細節部分都屬非設計區域，細節的計算精度并不影響主體設計區域的拓撲優化，所以體素化網格適用于本文對懸架控制臂的拓撲優化.

1.2 免組裝的壓縮共軛梯度法

拓撲優化中的迭代過程需要進行多次有限元求解，本文將基于壓縮共軛梯度法的免組裝有限元算法引入到拓撲優化過程中，可以提高每次有限元分析的速度，從而大幅縮短整個拓撲優化過程的時間.

免組裝（Assembly-free）有限元法，即總剛矩陣免組裝的有限元法，最初是Hughes等[15]在1983年提出的，隨著并行算法的發展，這種方法也得到了改進[17].免組裝有限元方法的基本概念是單元剛度矩陣不用組裝成總體剛度矩陣，而是在單元層面進行稀疏矩陣向量乘法.換而言之是將“組裝然后相乘”的過程：

變為“相乘然后組裝”：

式中：K為總體剛度矩陣；d為位移向量.

共軛梯度法Conjugate Gradient （CG）是求解大型稀疏線性方程的一種迭代算法，迭代過程中最占用計算時間的是矩陣向量乘法運算Kd，其大部分的內存占用來自存儲和提取剛度矩陣.如上節所述，由于結構使用統一的單元進行網格劃化，所有單元的形狀和尺寸是一樣的，所以單元剛度矩陣是一樣的，不需要組裝并存儲總體剛度矩陣K，而只需要儲存單個單元剛度矩陣Ke.這將大大減少內存占用，提高矩陣向量乘法運算的速度，從而提高迭代算法的計算速度.

壓縮共軛梯度法Deflated Conjugate Gradient （DCG）是一種加速的迭代算法[20].它將有限元網格的點劃分成少數的幾塊，把每塊網格當作剛體處理，構造出壓縮空間.在某塊里的一個點的位移表示為

式中：（u0，v0，w0， θx， θy， θz）T是此塊在6個自由度上的剛體運動.（x，y，z）是該塊中一點相對此塊幾何中心的坐標.通過所有點的相對坐標，構造出壓縮矩陣W，于是有：

式中：d有3N個自由度（N是所有點個數）；λ是6G個與塊相關的自由度（G是分塊的個數）.可以使用壓縮空間矩陣W進行共軛梯度運算.（具體推導及理論分析可參考文獻[21]）.由于分塊的數量G遠小于節點數量N，所以壓縮矩陣的尺度比剛度矩陣的小，在迭代過程中能夠提高矩陣向量乘法運算的速度，從而對迭代過程起到加速作用.同時，這種壓縮共軛梯度算法也能使用Assembly-free方法，就像在式（2）中的Kd運算不需要組裝總體剛度矩陣，總體壓縮矩陣W也不需要組裝，而是采用“相乘然后組裝”的方式：

這種免組裝的壓縮共軛梯度方法能夠高效地處理高達幾百萬自由度的大型有限元問題[17].

如圖 2所示，本文將懸架控制臂的網格模型分為200個組.使用免組裝的壓縮共軛梯度法求解靜力學問題，并得到位移和應力場.

2 多工況懸架控制臂拓撲優化

2.1 拓撲靈敏度控制的水平集優化算法

不同于利用偽密度的SIMP方法，本文使用的拓撲優化方法基于拓撲靈敏度.拓撲靈敏度是當拓撲上發生極小的改變時，目標量的變化率.這是由Eschenauer[22]最早研究的，隨后諸多學者[23-25]對其進行了擴展研究.

這里通過圖 3中的二維例子對拓撲靈敏度進行闡述，研究的目標量是Q，假設結構域某處p去除一個極小的半徑為r的小孔，結構的變形將會發生改變，所關心的目標量Q也會改變，拓撲靈敏度TQ定義為[22]：

本文的目標量是柔度J，從公式（6）可以推導出關于柔度拓撲靈敏度[26]的解析表達式：

式中：TJ為關于柔度J的拓撲靈敏度；p表示網格中的某點；σ為應力張量；ε為應變張量；v為泊松比.

設計域內所有點的拓撲靈敏度構成一個靈敏度場，由定義可知，這個靈敏度場中具有相對較高值的區域表示這個部分對于目標量Q相對重要.使用此拓撲靈敏度場作為水平集，可以用來引入孔洞，確定新的結構域.例如圖 4中，引入了一個任意閾值為τ=0.02的“切割”平面，通過式（8）可以確定圖 5所示的拓撲結構Ωτ：

式中的閾值τ是通過當前所需的體積比確定的.結構域Ωτ是所有拓撲靈敏度超過τ的點的集合.

然而直接得到的結構域Ωτ并不一定是pareto最優解[13]，需要反復進行以下3步：1）對生成的結構域進行有限元分析；2）重新計算拓撲靈敏度；3）根據當前目標體積分數確定新的閾值τ，并生成新結構域.通常這個過程需要3到4次迭代能夠收斂[12].收斂之后，可以繼續降低當前目標體積分數，重復上述過程，直至得到最終設計要求的體積分數f V0.總體的流程如圖 6所示，優化算法的步驟概括為：

①從初始結構Ω=Ω0開始，初始體積V=V0；

②對初始結構Ω0進行有限元分析，通過公式（7）計算拓撲靈敏度；

③按給定的體積減少步長ΔV，確定當前目標體積V=V-ΔV；

④按當前目標體積和拓撲靈敏度場，確定水平集參數τ，使新結構Ωτ的體積等于當前目標體積V；

⑤進行迭代處理：對新結構Ωτ進行有限元分析、計算拓撲靈敏度、得到新結構……直到目標函數J收斂；

⑥判斷當前的體積V是否達到最終設計要求的體積fV0，如果沒有達到，繼續按照步長ΔV降低目標體積分數，返回步驟②；

⑦當前體積達到設計要求的體積分數時，算法終止.

2.2 多工況優化模型

多工況條件下懸架控制臂的拓撲優化模型為

式中：J為綜合目標函數；m為工況總數；Ji為第i個工況的柔度；ωi為第i個工況的權重；V為優化后的體積；V0為結構初始體積；f為體積約束的百分比.

根據各工況的權重系數，可以構造一個新的多工況條件下的拓撲靈敏度：

式中：Ti為第i個工況下的拓撲靈敏度.

各工況的權重系數可以通過經驗法、層次分析法等確定.由于如何選擇權重系數并不是本文研究重點，本文重在使用相同的工況和權重系數設置與基于SIMP方法的商用軟件作對比.所以本文考慮表 1所示的穩態轉向和直線制動兩種最基本的工況[27]，假設兩種工況的權重系數都為0.5.

對于本文考慮的麥弗遜懸架的下控制臂，在前襯套A和后襯套B通過鉸接副與車架相連，在外球銷點C通過球形副與轉向節相連.主要在加速、制動時承受縱向力Fx，以及在轉向時承受側向力Fy.對于垂向力，下控制臂只是抵消前后橡膠襯套扭轉變形時的一些結構反力，而垂向力主要由懸架彈簧來承受，控制臂承受的垂向力的數量級遠小于縱向力及側向力，所以在分析下控制臂時通常不考慮垂向力Fz.分析麥弗遜懸架控制臂時通常固定前襯套X，Y，Z 3個方向平動自由度，后襯套Y，Z方向平動自由度，外球銷點Z方向平動自由度.制動、轉向時的縱向、側向力分為兩個工況施加到外球銷點上.

2.3 加工約束

通過拓撲優化方法進行性能最優化設計的結果常常會出現中空的復雜結構，不適合傳統加工方法.目前，大多數汽車零部件還是采用傳統的方法加工，所以此懸架控制臂的拓撲優化中需要考慮加工制造約束.為了使控制臂結構易于制造加工，在Z方向添加方向約束.具體方法就是對Z方向的各單元的拓撲靈敏度進行額外處理，使外側單元的拓撲靈敏度不大于內側單元的拓撲靈敏度，這樣就能保證在拔模方向上不會出現中空的結構.值得注意的是，由于使用了體素單元劃分網格，網格的排列十分工整，有利于編程實現加工制造約束.

3 優化結果

使用本文方法基于C++語言開發的程序和Hyperworks分別進行拓撲優化，設置相同的材料參數，彈性模量210 GPa，泊松比0.3，使用前文所述的工況設置，網格模型自由度為280 000，目標體積分數為50%.優化后的結果分別如圖 7 （a） （b）所示.圖 8給出了優化過程中兩種工況下的柔度變化曲線，以及優化過程中的一些拓撲結構和應力云圖.

兩種方法的最優拓撲略有不同，但除了一些細小結構的區別，主要的材料分布趨勢是近似的.根據最優拓撲提供的參考，對結果進行幾何重構后如圖9所示，性能對比如表2所示.

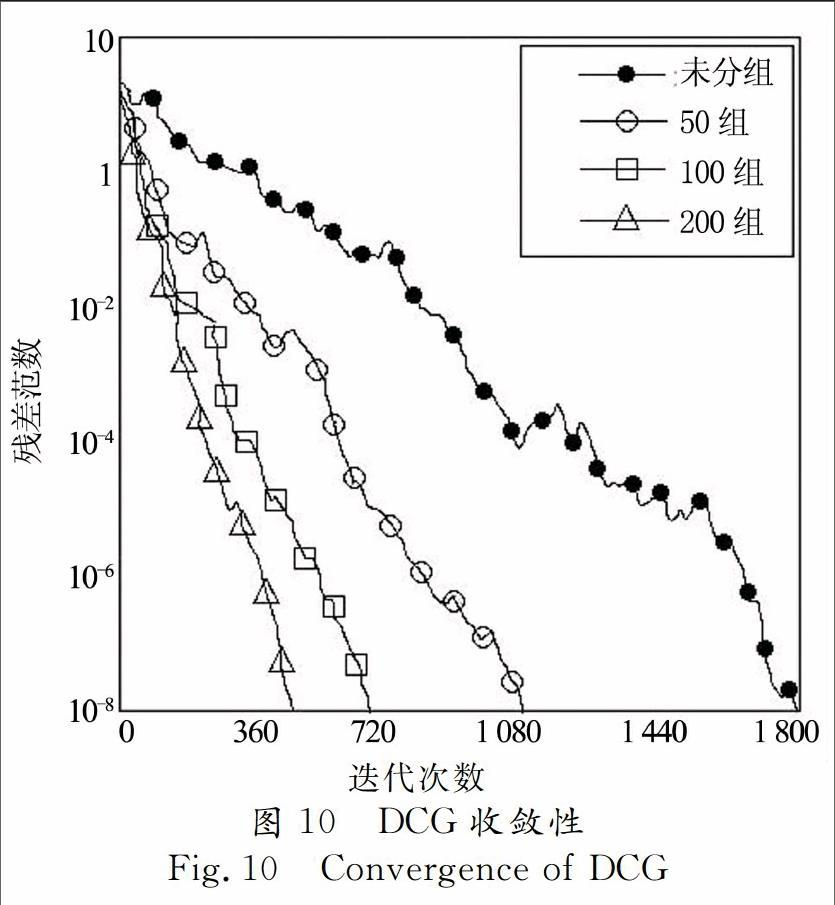
通過表 2中各工況的柔度、最大位移、最大應力的對比可知，兩種結構的性能接近，且本文方法優化的結構性能略優于Hyperworks優化的結果.而在計算時間上，兩種方法有很大不同，本文方法是Hyperworks的26 %，可見對于大自由度的模型，本文方法有明顯的速度優勢.這主要是由于DCG算法對有限元求解的加速作用.圖10表明了使用不同分組數的DCG算法的收斂性，分組數量的不同導致DCG運算收斂所需的迭代次數不同.如圖所示，分成200組比未分組的CG運算所需的迭代次數大幅降低，這意味著單次有限元分析所需的時間大幅降低，從而縮短了整個拓撲優化過程的時間.不同分組數下相應的拓撲優化時間如表3所示.

迭代次數

此外，對于復雜結構，商用軟件需要人工進行幾何分解、網格劃分、網格質量檢查等步驟，直到滿足商用軟件的特定要求后才能開始拓撲優化.而本文方法采用體素化網格實現自動網格劃分，在拓撲優化的前處理階段就可以節省大量的時間.

4 結 論

本文將一種基于拓撲靈敏度的拓撲優化算法與免組裝壓縮共軛梯度法結合，提高了大型三維拓撲優化的速度，通過添加多工況優化和加工約束功能，使其更適合實際工程應用.通過懸架控制臂的多工況優化，與基于SIMP方法的商用軟件對比，結果表明，該算法具有明顯的速度優勢，且能獲得性能相近的結構.由于拓撲優化是初始的概念設計，體素化網格的精度局限性對拓撲優化結果并不會產生很大影響，而速度優勢可以在前處理階段以及拓撲優化階段得到很好的發揮.在未來的研究中，可以拓展更全面的優化功能，使該算法能更好地滿足實際工程應用的要求.

參考文獻

[1] SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural & Multidisciplinary Optimization， 2001， 21（2）：120-127.

[2] HUANG X， XIE Y M. A new look at ESO and BESO optimization methods[J]. Structural & Multidisciplinary Optimization， 2008， 35（1）：89-92.

[3] MUNK D J， VIO G A， STEVEN G P. Topology and shape optimization methods using evolutionary algorithms： a review[J]. Structural & Multidisciplinary Optimization， 2015， 52（3）：613-631.

[4] MEI Y， WANG X. A level set method for structural topology optimization and its applications[J]. Advances in Engineering Software， 2004， 35（7）：415-441.

[5] DIJK N P V， MAUTE K， LANGELAAR M， et al. Level-set methods for structural topology optimization： a review[J]. Structural & Multidisciplinary Optimization， 2013， 48（3）：437-472.

[6] BENDSE M P， SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics， 1999， 69（9/10）： 635-654.

[7] ROZVANY G I N. A critical review of established methods of structural topology optimization[J]. Structural & Multidisciplinary Optimization， 2009， 37（3）：217-237.

[8] 祝小元，方宗德，申閃閃，等. 汽車懸架控制臂的多目標拓撲優化[J]. 汽車工程， 2011， 33（2）： 138-141.

ZHU Xiaoyuan， FANG Zongde， SHEN Shanshan， et al. Multi-objective topology optimization for the control arm of vehicle suspension[J]. Automotive Engineering， 2011， 33（2）： 138-141. （In Chinese）

[9] 蘭鳳崇，張浩鍇，王家豪，等. 汽車轉向節拓撲優化方法研究及應用[J]. 汽車工程， 2014， 36（4）： 464-468.

LAN Fengchong， ZHANG Haokai，WANG Jiahao， et al. Study and application of topology optimization technique for vehicle steering knuckles[J]. Automotive Engineering， 2014， 36（4）： 464-468. （In Chinese）

[10]朱劍峰，林逸，施國標，等. 考慮工程約束的發動機懸置支架拓撲優化[J]. 汽車工程， 2014， 36（12）： 1508-1512.

ZHU Jianfeng， LIN Yi， SHI Guobiao， et al. Topology optimization of engine mount bracket with consideration of engineering constraints[J]. Automotive Engineering， 2014， 36（12）： 1508-1512. （In Chinese）

[11]張偉， 侯文彬， 胡平. 基于拓撲優化的電動汽車白車身優化設計[J]. 湖南大學學報：自然科學版， 2014，41（10）：42-48.

ZHANG Wei， HOU Wenbin， HU Ping. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University：Natural Sciences， 2014，41（10）：42-48. （In Chinese）

[12]SURESH K. Efficient generation of large-scale pareto-optimal topologies[J]. Structural & Multidisciplinary Optimization， 2013， 47（1）：49-61.

[13]SURESH K. A 199-line matlab code for pareto-optimal tracing in topology optimization[J]. Structural & Multidisciplinary Optimization， 2010， 42（5）：665-679.

[14]INNA T， KRISHNAN S. Efficient generation of pareto-optimal topologies for compliance optimization[J]. International Journal for Numerical Methods in Engineering， 2011， 87（12）：1207-1228.

[15]HUGHES T J R， LEVIT I， WINGET J. An element-by-element solution algorithm for problems of structural and solid mechanics[J]. Computer Methods in Applied Mechanics & Engineering， 1983， 36（2）：241-254.

[16]YADAV P， SURESH K. Assembly-free large-scale modal analysis on the graphics-programmable unit[J]. Journal of Computing & Information Science in Engineering， 2013， 13（1）：1-11.

[17]YADAV P， SURESH K. Large scale finite element analysis via assembly-free deflated conjugate gradient[J]. Journal of Computing & Information Science in Engineering， 2014， 14（4）： 1-9.

[18]KARABASSI E A， PAPAIOANNOU G， THEOHARIS T. A fast depth-buffer-based voxelization algorithm[J]. Journal of Graphics Tools， 1999， 4（4）： 5-10.

[19]DSTER A， PARVIZIAN J， YANG Z， et al. The finite cell method for three-dimensional problems of solid mechanics[J]. Computer Methods in Applied Mechanics & Engineering， 2008， 197（45/48）：3768-3782.

[20]AUBRY R， MUT F， DEY S. Deflated preconditioned conjugate gradient solvers for linear elasticity[J]. International Journal for Numerical Methods in Engineering， 2011， 88（11）： 1112-1127.

[21]SAAD Y， YEUNG M， ERHEL J， et al. A deflated version of the conjugate gradient algorithm[J]. Siam Journal on Scientific Computing， 1998， 21（5）： 1909-1926.

[22]ESCHENAUER H A， KOBELEV V V， SCHUMACHER A. Bubble method for topology and shape optimization of structures[J]. Structural & Multidisciplinary Optimization， 1994， 8（8）：42-51.

[23]PARS J， NAVARRINA F， COLOMINAS I， et al. Topology optimization of continuum structures with local and global stress constraints[J]. Structural & Multidisciplinary Optimization， 2010， 39（4）：419-437.

[24]STOLPE M， STIDSEN T. A hierarchical method for discrete structural topology design problems with local stress and displacement constraints[J]. International Journal for Numerical Methods in Engineering， 2007， 69（5）：1060-1084.

[25]RAMANI A. Multi-material topology optimization with strength constraints[J]. Structural & Multidisciplinary Optimization， 2011， 43（5）：597-615.

[26]GIUSTI S M， NOVOTNY A A， PADRA C. Topological sensitivity analysis of inclusion in two-dimensional linear elasticity[J]. Engineering Analysis with Boundary Elements， 2008， 32（11）：926-935.

[27]上官文斌，蔣翠翠，潘孝勇. 汽車懸架控制臂的拓撲優化與性能計算[J]. 汽車工程， 2008， 30（8）： 709-712.

SHANGGUAN Wenbin， JIANG Cuicui， PAN Xiaoyong. Topology optimization and performance calculation for control arm of vehicle suspension[J]. Automotive Engineering， 2008， 30（8）： 709-712. （In Chinese）