高速永磁無刷直流電機無位置全轉速控制策略

陳少華， 劉剛， 鄭世強， 郭金超

(1.北京航空航天大學 慣性技術國防科技重點實驗室，北京 100191；2.北京航空航天大學 新型慣性儀表與導航系統技術國防重點學科實驗室，北京 100191；3.北京市高速磁懸浮電機技術及應用工程技術研究中心，北京 100191)

高速永磁無刷直流電機無位置全轉速控制策略

陳少華1，2，3， 劉剛1，2，3， 鄭世強1，2，3， 郭金超1，2，3

(1.北京航空航天大學 慣性技術國防科技重點實驗室，北京 100191；2.北京航空航天大學 新型慣性儀表與導航系統技術國防重點學科實驗室，北京 100191；3.北京市高速磁懸浮電機技術及應用工程技術研究中心，北京 100191)

針對高速磁懸浮大功率永磁無刷直流電機無位置傳感器起動問題，分析了高速磁懸浮無刷直流電機運行時導通相磁鏈函數與相電壓的精確表達式，給出了轉子位置和電機磁鏈的函數方程，分析了高速磁懸浮無刷直流電機低速時轉子位置難以檢測的原因。據此分析提出了一種基于高速電機繞組磁鏈函數的新型無位置控制G函數方法，以換相前后非換相相電流幅值等值為控制目標，以G函數換相閾值為控制量，通過PI調節來保證相位可靠校正，實驗驗證了該閉環校正方法應用于磁懸浮鼓風機無刷直流電機時，在20 000 r/min范圍內能夠對換相信號誤差進行了實時補償，實現全轉速運行。

磁懸浮鼓風機；無刷直流電機；無位置傳感器；G函數；換相閾值

0 引 言

高速磁懸浮永磁無刷直流電機以其功率密度高、轉子無摩擦損耗，噪聲低、重量輕等優點，被廣泛應用于鼓風機、壓縮機等高端工業制造裝備中。

傳統的無刷直流電機安裝的霍爾傳感器增加了電機的體積和成本、可靠性低、抗擾動能力弱，嚴重限制了其應用發展[1]。近年來提出的無刷直流電機無位置傳感器控制策略從根本上解決了傳遞霍爾傳感器的弊端。因此無刷直流電機無位置傳感器研究具有重要意義。

無位置傳感器控制策略發展至今，主要包括反電勢法(EMF)[1-3]，三次諧波法[4-5]，反電勢積分法[6-7]，磁鏈估測法[8]，續流二極管法[9]，智能控制算法[10-11]等。其中反電動勢法目前應用最為廣泛，但低速時反電動勢幅值難以檢測，高速時低通濾波、電路延時等因素導致位置信號產生誤差，嚴重影響電機性能。

文獻[12]研究了端電壓法檢測誤差，通過相電流偏差判定轉子位置超前或滯后，提出一種轉子位置閉環校正方法，但檢測電路對大功率電機不太合適；文獻[13]通過硬件電路實現相位固定延時90°得到轉子位置信號，但高速電機滯后相位難以實施補償；文獻[11]針對小電感電機，將三相H橋結構引入到電機的三相六狀態控制中，實現了反電動勢過零點檢測，但實現較為復雜；文獻[14-19]基于鐵心飽和效應或者電機凸極效應，主要研究了電壓注入式控制方法，判定轉子初始位置進而實現啟動，但本實驗電機凸極效應不明顯，難以實現；文獻[20]采用新型反電動勢檢測方法，消除了濾波電路帶來的誤差，但是當續流超過30°時不能檢測到反電動勢過零點，可靠性不高。

針對高速磁懸浮鼓風機用無刷直流電機的定子電阻和電感極小的特點，分析傳統無位置傳感器控制方法低速時相位難以檢測的原因，在傳統無位置控制G函數方法的基礎上，提出了一種優化的繞組磁鏈函數無位置控制方法，以換相前后非換相相電流微分等值為控制目標，以G函數換相閾值為控制量，通過PI調節來保證相位可靠校正

通過仿真和實驗驗證了該閉環校正方法應用于磁懸浮鼓風機無刷直流電機時，在20 000 r/min范圍內能夠對換相信號誤差進行了實時補償，實現全轉速運行。

1 無刷電機數學模型與換相分析

1.1 高速無刷直流電機數學模型

采用的高速磁懸浮無刷直流電機驅動系統拓撲結構，如圖1所示。

圖1 高速磁懸浮無刷直流電機驅動系統拓撲結構Fig.1 Topological structure of the brushless DC motor based on Buck Converter

假設電機定子三相完全對稱，各相繞組R，L參數完全相同；忽略定子繞組電樞反應的影響；電機氣隙磁導均勻，磁鋼性能一致，忽略磁路飽和，渦流損耗、鐵耗、漏感及電流飽和效應。無刷直流電機相電壓方程如下所示

(1)

其中：Ua、Ub、Uc分別為電機三個相電壓；ia、ib、ic分別代表電機三相線(相)電流；ea、eb、ec分別代表電機三個相反電勢；R、L分別代表相電阻、電感。

1.2 無位置傳感器轉子位置檢測分析

傳統的基于電機反電動勢無位置控制方式通過檢測電機不導通相的端部電壓，經過濾波處理后與電機繞組中線電壓進行比較，得到反電動勢的過零點信號，延時30°作為轉子換向信號。但電機在靜止或者轉速很低時，電機端部電壓為零或非常低，需要通過開環外同步的方法將電機強拖到一個較高的轉速。用于端部電壓檢測的濾波電路和電壓比較電路如圖2所示。

無刷直流電機采用PWM調制時，電磁轉矩為

(2)

式中：Te為電機電磁轉矩，ωm為電機角速度，e為相反電動勢，i為相電流，E為反電動勢幅值，對于同一臺電機。從式(2)知，隨電流增大，電機電磁轉矩增大，當電磁轉矩大于負載轉矩時，電機開始旋轉，實現啟動。等效電路如圖2所示，Ud為電機定子繞組兩端的電壓，L為等效電感，R為等效電阻，e為導通相等效反電動勢。

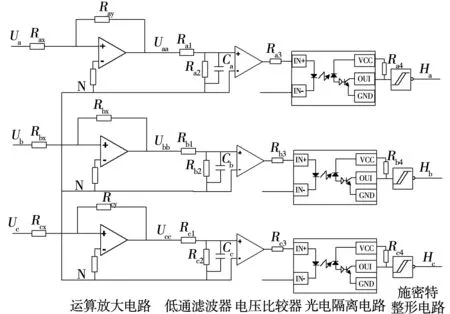
圖2 電機非導通相端部電壓檢測電路Fig.2 Voltage detection circuit of motor phase

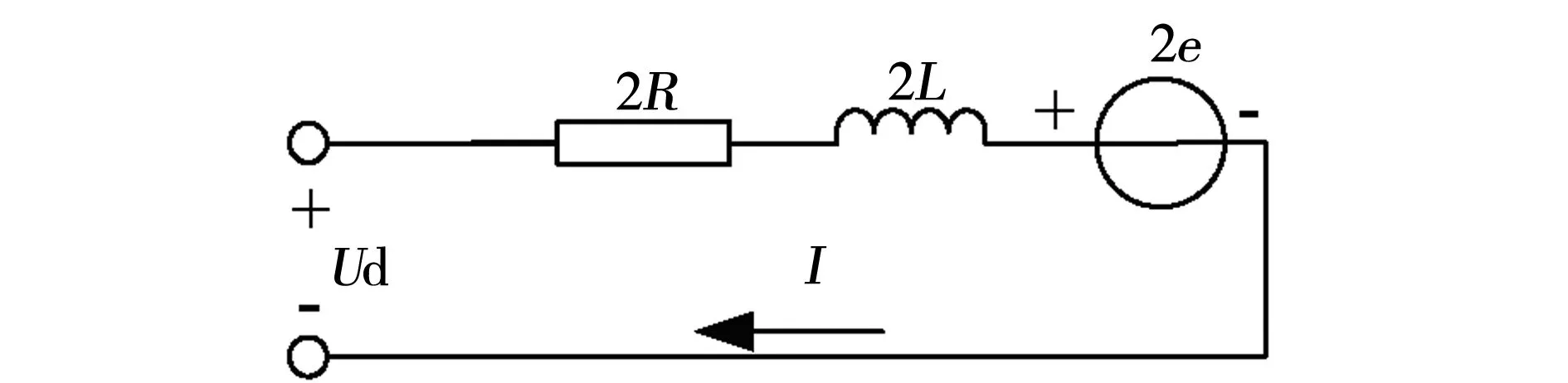
圖3 電機啟動時等效電路Fig.3 Equivalent circuit of motor start-up

其等效電流幅值為

(3)

當采用單管PWM控制啟動，在電機轉速很低時，等效反電動勢e≈0，且ω≈0。以實驗電機為例，Ud=100 V，R≈1.5×10-3Ω，調制頻率為5kH，最小占空比為0.1時，，瞬間啟動電流幅值 ，導致功率器件損壞。單管PWM調制啟動時實驗波形如圖3所示，啟動相電流峰峰值400A，啟動后PWM調制高頻噪聲易干擾轉子位置信號，導致電機錯誤換相，產生相電流波動，電流波動引起電機轉矩脈動，易導致啟動失敗，同時易產生電機噪聲，電機渦流損耗增大，影響電機壽命。

如圖4所示，電機在“三段式自啟動”階段,相電壓波形畸變嚴重，相電流幅值過大，母線電壓隨PWM調制波動。如圖5所示，由于采用PWM斬波調整定子側電壓，轉子位置信號中包含有高頻干擾信號，會導致轉子“誤換相”。此時，相電流出現尖峰，出現電機負轉矩，電機噪聲增大，嚴重時，電機堵轉，損壞功率器件。

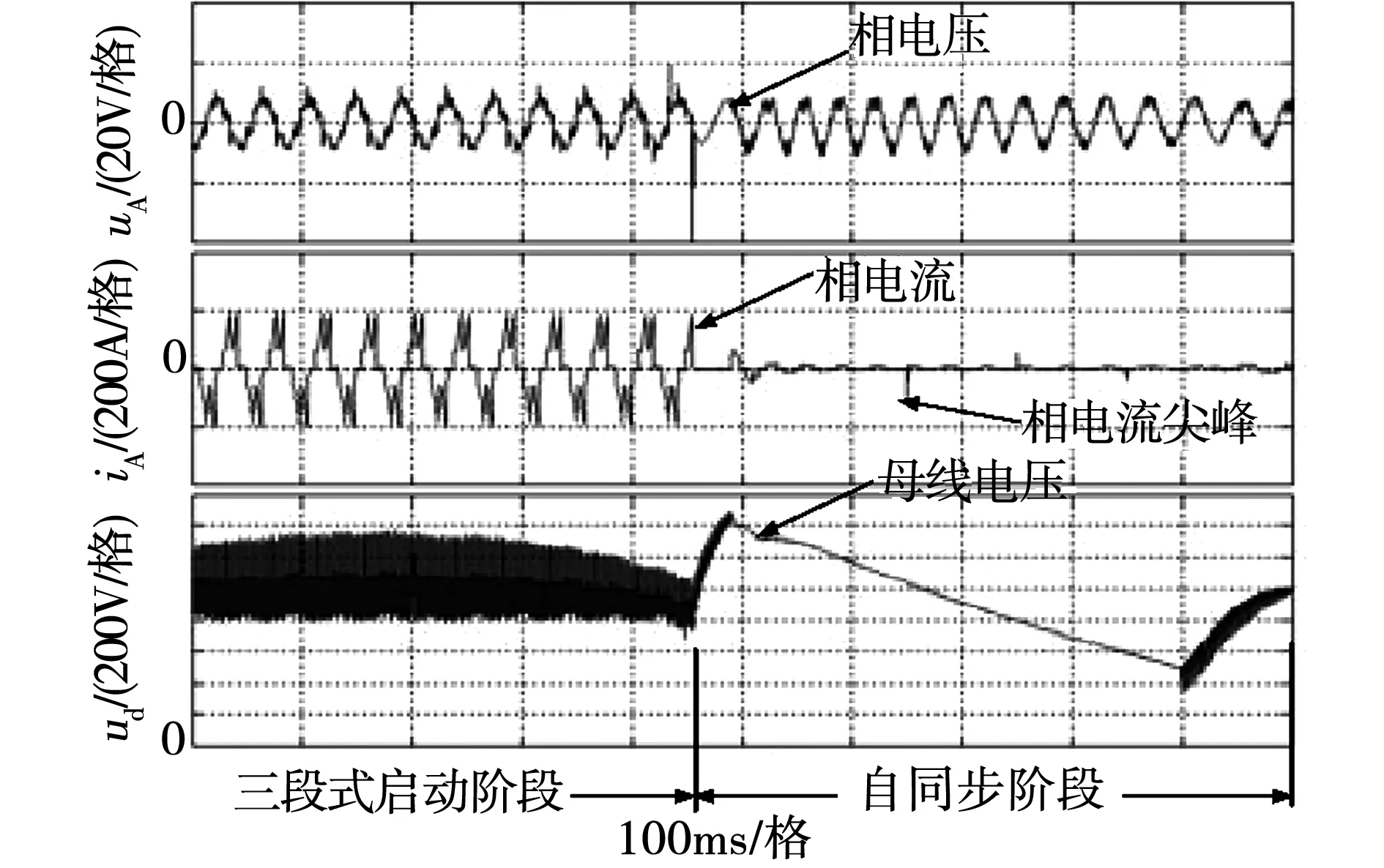
圖4 電機啟動時相電壓，相電流和母線電壓波形Fig.4 Phase voltage,phase current and bus voltage in start-up

圖5 PWM調制電機啟動時轉子位置信號Fig.5 Rotor position signal in start-upby PWM modulated

因此，針對極小電阻電感高速磁懸浮無刷直流電機需要專門設計啟動控制策略和相位校正策略。

2 電機換相特性分析

無刷直流電機反電動勢表示為

(4)

其中：n=a,b,c，ke為反電動勢系數。

將式(4)代入式(1)可得，

(5)

為便于計算，通過類比式(5)，線電壓方程式為

(6)

同理可得

(7)

(8)

fxyr(θ)為反映轉子位置的磁鏈形式函數。由式(6)得

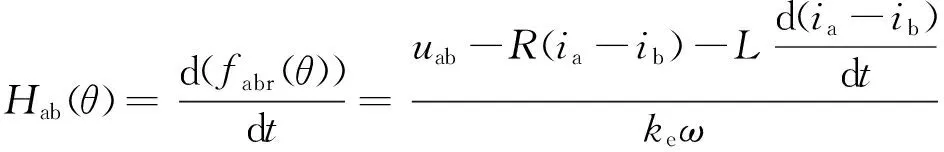
(9)

Hab(θ)是一個關于轉子位置的函數，可用于電機轉子位置的估算。但由于函數中包含轉速因子，在低速時轉速不平穩，高速時產生誤差累計。為此，將反電動勢相鄰兩式相除以消去轉速項，可得

(10)

(11)

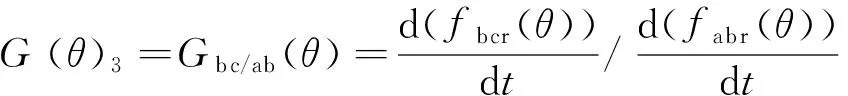
(12)

G(θ)函數可以通過測量電壓、電流和相關參數信息得到。由于函數中不包含速度變量，所以它是速度無關的函數，可實現任意速度的轉子位置估計。可得H(θ)函數、G(θ)函數、相電流和位置信號的波形圖如圖6所示。

如圖所示，在一個換相周期內，線性函數H(θ)依次連續相比，可得到與速度無關的G(θ)函數，其換相點就是G(θ)函數的最大峰值點。但是檢測電路必然導致相位延遲，因此需要在G(θ)函數的最大峰值點之前換相，假設F為換相閾值，當G(θ)函數值大于F時即開通換相信號。由于G(θ)函數與電機轉速無關，因此在電機轉速很低時仍然可以通過計算G(θ)函數得到電機轉子位置信號，實現換相。在高速時由于檢測電路延時和計算誤差易導致G(θ)函數計算偏差，因此需要閉環校正換相閾值F，實現高效精確換相。

圖6 H(θ)函數、G(θ)函數、相電流和位置信號Fig.6 H(θ)function,G(θ)function,phase current and position signal

由于電機電感的存在，換相電流將會出現兩個階段。第1個階段由于關斷相電感中的電流不能立刻突變，將通過二級管進行續流。大功率高速磁懸浮電機，電機電阻和電感都非常小。所以，電機換相時間接近0，可以忽略。第2個階段是換相結束后相電流已經建立，B+，A-導通。換相第1階段，VT3、VT4以及與VT5反并聯的二極管同時導通，電路狀態示意圖如圖7所示。

圖7 正常換相第1階段電路狀態示意圖Fig.7 Schematic diagram of the state of the normal commutation circuit

三相相反電勢ea、eb、ec方程分別為：

(13)

E代表反電勢有效值。

當VT3、VT4導通，此時電路狀態示意圖如圖6(b)所示：由ia+ib=0，ic=0，和式(1)得到

(14)

求解式(14)得到

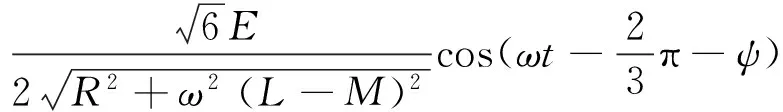
(15)

由式(15)可看出，正常換相時，時間常數τ非常小，可忽略不計，式(15)可以簡化為

(16)

正常換相時，ib的波形如圖8所示，從中可看出換相前后非換相相電流幅值相等。超前換相時，B+，A-導通，C-關斷，ud=ub-ua，超前ε′(ε′>0)角度換相時，結合ia+ib=0，ic=0，和式(1)得到

(17)

求解式(17)得到

(18)

由于時間常數τ非常小，同理式(18)可以簡化為：

(19)

超前換相ε′角度時，ib對應的波形圖如圖8(b)所示，從中可以看出：超前換相時，換相前后非換相相電流幅值不相等，超前換相角度越大，幅值差別越大，電流波動幅值越大。

圖8 正常換相第2階段ib與線電勢的關系圖Fig.8 Relationship of ib and line back-EMF in the second stage of normal commutation

滯后換相時電流表達式為：

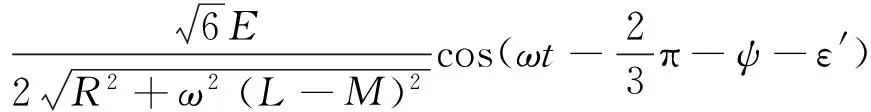
(20)

同理當B+，A-導通時式(20)可以簡化為

(21)

超前換相ε′角度時，ib對應的波形圖如圖8(c)所示，從中可以看出：超前換相時，換相前后非換相相電流幅值不相等，滯后換相角度越大，幅值差別越大。

綜上所述：超前或者滯后換相都會使電流脈動加大，且超前角或者換相角越大，電流脈動越大。

3 無位置傳感器全轉速控制策略

以G(θ)函數值閾值F為控制量，以非換相相在換相前后電流幅值偏差相等為控制目標，提出一種校正無位置傳感器全轉速控制策略。新型控制系統如圖9所示，整個控制系統主要由轉速環、電流環、反電勢換相信號檢測、換相策略控制等環節構成。電機經過預定位和啟動之后，切換到無位置工作狀態，與傳統的無刷直流電機調速系統相比，給出的控制系統針對極小電感電機啟動困難、高速相位誤差大等問題實現了全轉速運行。

圖9 帶有換相信號位置偏差補償的新型調速系統Fig.9 New speed control system with the commutation error compensation

4 實驗驗證與分析

在以上分析基礎上搭建實驗平臺，采用TI公司的DSPTMS320LF28335控制芯片，PWM調制頻率10kH，逆變橋采用英飛凌6PS18012E4FG35689模塊，采用4極電機，額定轉速20 000 r/min，額定轉矩150 N·m，額定功率100 kW，額定電流210 A。實驗平臺如圖10所示。

圖10 系統實現框圖Fig.10 System block diagram

當電機靜止或速度很低時，無法檢測到換相信號，采用“三段式起動”方法。首先任意導通兩相繞組，為防止力矩為零或力矩極小的情況，再導通相鄰兩相繞組，兩次定位，保證將轉子定位在固定的位置上。然后采用升頻升壓的方式逐步提升電機轉速。直到得到準確的G函數，確定準確的換相信號時，切換到無位置閉環校正換相控制階段。G函數波形，換相信號波形和相電流波形如圖13所示。

圖11 G函數閉環校正啟動時電壓，電流和轉子位置信號Fig.11 Voltage,current and rotor position signal by G function

由圖11可知,先由“三段式起動”，采用兩步定位法，確定轉子位置，然后采用升頻升壓的方式逐步提升電機轉速，直到G函數被精確檢測到，切換到無位置閉環校正換相控制階段。

針對本實驗室電機采用傳統的“三段式起動”時，相電流，相電壓，位置信號波形如圖12所示。

圖12 “三段式起動”，相電流，相電壓，位置信號波形Fig.12 Phase voltage,phase current and rotor position signal in traditional way

如圖12所示，在電機外同步強推時,由于采用PWM調制,高頻PWM信號導致位置信號包含大量高頻干擾信號，易換相失敗；且由于本實驗電啟動負載轉矩很大，需要設計復雜的啟動曲線，啟動階段當負載變化時極易導致啟動失敗。

為驗證G函數閉環校正控制策略在系統負載變化時的有效性，當電機運行時，突然改變電機負載，圖13(a)為電機負載突然增大時，電機相電壓，相電流和直流母線電壓波形，圖13(b)為電機負載突然減小時，電機相電壓，相電流和直流母線電壓波形。

由圖13可知,在電機由外同步強推到自同步切換時,電機負載突變時會影響電機切換時間，當電機負載突然增大時，電機相電流增大，電機轉速降低，此時無法，故電機仍處于強推狀態，繼續升速，直至到號，實現自同步切換；當電機負載突然變小時，電機相電流減小，電機轉速增大，當G函數信號能被精確檢測到時，實現自同步切換。該控制策略在啟動階段具有魯棒性。

采用軟件濾波在電機轉速達到3 000 r/m以上時，采用PWM調制會造成嚴重的相位滯后，由于采用軟件濾波屏蔽啟動時的高頻干擾信號，高速時，濾波產生的延時導致轉子位置信號無法精確提取，相電壓和相電流波形圖發生畸變，嚴重時導致電機轉子位置信號提取錯誤，產生誤換相，發生電機堵轉，損壞功率器件。為此在高速時，采用PAM控制，且退出軟件濾波，按照G函數閉環校正控制策略實時補償轉子位置信號，電機轉速在6 000 r/min和20 000 r/min時，電機相電壓和相電流波形如圖14所示。

圖13 G函數校正策略下電機負載突然變化時，相電壓、相電流和直流母線電壓波形Fig.13 Phase voltage and phase current waveform when the motor load suddenly changed by G function

圖14 電機在6 000 r/min和20 000 r/min時，相電壓和相電流波形圖Fig.14 Phase voltage and phase current waveforms of the motor in 6 000 r/min and 20 000 r/min

由圖14可知，電機轉速在6 000 r/min和20 000 r/min時，電機相電壓和相電流波形對稱，實現轉子位置信號精確補償。

圖15是n=8 000 r/min時電機帶載三相電流，其中圖15(a)是超前換相時的三相電流，此時換相前電流幅值小于換相后的電流幅值，圖15(b)是滯后換相時的三相電流，此時換相前的電流幅值大于換相后的電流幅值，圖15(c)是采用G函數閉環校正之后的三相電流，經過閉環校正之后，三相電流的波形對稱，精確補償了換相誤差角度。

圖15 n=8 000 r/min三相電流波形Fig.15 Three-phase current waveform of 5 000 r/min

圖16是n=20 000 r/min時電機帶載三相電流，圖16(a)是超前換相時的三相電流，圖16(b)是滯后換相時的三相電流，圖16(c)是采用閉環校正之后的三相電流，經過閉環校正之后，電機準確換相，換相誤差被校正。

圖16 n=20 000 r/min三相電流波形Fig.16 Three-phase current waveform of 20 000 r/min

5 結 論

本文采用的基于G函數的無位置換相閉環校正策略能夠保證電機小電流安全啟動，高速平穩運行，精確補償了換相誤差，硬件電路實現簡單。

1)給出高速大功率磁懸浮電機無位置啟動電流幅值巨大的原因，分析了基于線反電動勢的無位置傳感器正常換相與不準確換相時相電流的精確表達式；

2)提出一種基于G函數的低速無位置換相信號檢測新型控制方法，通過構造與電機轉速無關的G函數，將G函數閾值作為換相信號，有效的降低了大功率電機的無位置啟動切換轉速，減小了啟動電流。

3)實驗證明本文給出的基于G函數的無位置閉環校正策略能夠對換相信號偏差進行有效的、實時的補償，提高無位置傳感器的換相精確度，而且硬件電路實現相對簡單。

[1] 李志強,夏長亮,陳煒.基于線反電動勢的無刷直流電機無位置傳感器控制[J].電工技術學報,2010,25(7):39-25． LI Zhiqiang,XIA Changliang,CHEN Wei.A position sensorless control strategy for BLDCM based on line Back-EMF[J].Transactions of China Electro technical Society,2010,25(7):39-25．

[2] LIN C T,HUNG C W,LIU,C W.Sensorless control for four-switch three-phase brushless DC motor drive [J],in Conf.Rec.IEEE IAS Annu.Meeting,2006,4:2048-2053．

[3] 張磊,瞿文龍,陸海峰,等.一種新穎的無刷直流電機無位置傳感器控制系統[J].電工技術學報,2006,21(10):26-30,43. ZHANG Lei，QU Wenlong，LU Haifeng，et al． A novel sensorless control system of brushless DC motors [J]． Transactions of China Electro technical Society,2006,21(10):26-30,43.

[4] 韋鯤,任軍軍,張仲超.三次諧波檢測無刷直流電機轉子位置的研究[J].中國電機工程學報,2004,24(5):163-167. WEI Kun，REN Junjun，ZHANG Zhongchao．Research on the scheme of sensing rotor position of BLDCM based on the third harmonic component[J].Proceedings of the CSEE,2004,24(5):163-167.

[5] SHEN J X,IWASAKI S,Sensorless control of ultrahigh-speed PM brushless motor using PLL and third harmonic back-EMF[J].IEEE Trans.Ind.Electron.,2006,53(2):421-428.

[6] JAHNS T M,BECERRA R C,EHSANI M,Integrated current regulation for a brushless ECM drive[J].IEEE Trans.Power Electron.,1991,6(1):118-126.

[7] 周波,魏佳.反電勢邏輯電平積分比較法實現的無刷直流電機無位置傳感器控制[J].電工技術學報,2000,15(4):5-9. ZHOU Bo,WEI Jia.A new method of indirect sensing for rotor flux position of a sensorless brushless DC motor[J].Transactions of China Electro technical Society,2000,15(4):5-9．

[8] ERTUGRUL N,ACARNLEY P，A new algorithm for sensorless operation of permanent magnet motors [J]．IEEE Trans.Ind.Appl.,1994,30(1):126-133．

[9] 宋飛,周波,吳小婧,校正無位置傳感器無刷直流電機位置信號相位的閉環控制策略[J].中國電機工程學報,2009,29(12):52-56. SONG Fei,ZHOU Bo,WU Xiaojing．Closed loop vontrol method to correct position phase for sensorless brushless DC motor[J]． Proceedings of the CSEE,2009,29(12):52-56.

[10] 鄒繼斌,江善林,張洪亮.一種新型的無位置傳感器無刷直流電機轉子位置檢測方法[J].電工技術學報,2009,24(4):48-53. ZOU Jibin,JIANG Shanlin,ZHANG Hongliang.A novel method of detecting for rotor position of a sensorless brushless DC motor[J].Transactions of China Electro Technical Society,2009,24(4):48-53．

[11] 石堅,李鐵才,王孝偉,等.小電感無刷直流電動機三相H橋無位置傳感器控制方法[J].中國電機工程學報,2014,34(12):1905-1911. SHI Jian,LI Tiecai,WANG Xiaowei,et al.A sensorless control method of small inductance brushless DC motors with three-phase H-bridge connection[J].Proceedings of the CSEE,2014,34(12):1905-1911.

[12] 史婷娜,吳志勇,張茜,等.基于繞組電感變化特性的無刷直流電機無位置傳感器控制[J].中國電機工程學報,2012,32(27):45-52. Shi Tingna,WU Zhiyong,ZHANG Qian,et al.Sensorless control of BLDC motors based on variation behavior of winding inductances[J].Proceedings of the CSEE,2012,32(27):45-52．

[13] 王強,王友仁,孔德明,等.隱極式無刷直流電機轉子初始位置估計[J].中國電機工程學報,2012,32(33):105-110. WANG Qiang，WANG Youren，KONG Deming，et al．Initial rotor position estimation for non-salient pole brushless DC motors [J]．Proceedings of the CSEE,2012,32(33):105-110.

[14] 王高林,楊榮峰,李剛,等.基于高頻信號注入的 IPMSM 無位置傳感器控制策略 [J].電工技術學報,2012,27(11):62-67. WANG Gaolin,YANG Rongfeng,LI Gang．Position sensorless control strategy of IPMSM based on high frequency signal injection[J].Transactions of China Electro Technical Society,2012,27(11):62-67.

[15] SHAO Jianwen,NOLAN D,TEISSIER M,et al．A novel micro controller-based sensorless brushless DC(BLDC) motor drive for automotive fuel pumps[J].IEEE Trans.on Industry Applications,2003,39(6):1734-1740．

[16] PASQUESOONE G,MIKAIL R,HUSAIN I.Position estimation at starting and lower speed in three-phase switched reluctance machines using pulse injection and two thresholds[J].IEEE Transactions on Industry Applications,vol.47,No.9,pp.1724-1731,July,2011.

[17] 林明耀,劉文勇,周谷慶.無位置傳感器無刷直流電機短時脈沖定位加速方法[J].電機與控制學報,2011,26(09):80-86. LIN Mingyao，LIU Wenyong，ZHOU Guqing.A location and acceleration method of sensorless brushless DC motor Utilizing Short Voltage Pulse.Electiric Machines and Control，2011,26(09):80-86.

[18] 付敏,陳洋.U型單相永磁同步電機振動及噪聲的有限元分析[J].哈爾濱理工大學學報,2015,20(3):86 -90. FU Min,CHEN Yang.The vibration and noise finite elementanalysisi of U type single phase permanent magnet synchronous motor[J].Journal of Harbin University of Science and Technology,2015,20(3):86-90.

[19] JANG J H,SUL S K,HA J L.Sensorless drive of surface-mounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency,IEEE Transactions on Industry Applications,vol.39,no.4,pp.1031-1038,Mar.2003.

[20] YUAN L,XIAO F,SHEN J Q,et al.Sensorless control of high-power interior permanent magnet synchronous motor drives at very low speed,IET Electr.Power Appl.,2013,7,(3),pp.199-206.

(編輯：賈志超)

Sensorless full speed range control strategy of high-speed maglev brushless DC motor

CHEN Shao-hua1,2,3， LIU Gang1,2,3， ZHENG Shi-qiang1,2,3， GUO Jin-chao1,2,3

(1.School of Instrumentation Science and Optoelectronics Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China;2.Beijing Engineering Research Center of High-Speed Magnetically Suspend Motor Technology and Application,Beijing 100191,China; 3.University of Aeronautics and Astronautics,Beijing 100191,China)

This paper focuses on start-up strategy of high-speed maglev brushless DC Motor,and the accurate expressions of voltage and flux linkage have been obtained,and the functional equation of rotor position and motor flux linkage have been pointed out.The reason of the rotor position being difficult to be tested in the low speed of the high speed maglev brushless DC motor has been analyzed.A G function method of high speed maglev brushless DC motor has been proposed.This method took the equivalent phase current of non-commutation phase amplitude as the target and takes the phase current difference of non-commutation phase before and after the commutation as feedback amount,and corrected the commutation signals automatically through G function threshold by PI regulator.Experimental results show that the proposed sensorless full speed range control strategy can ensure the full speed range of 20 000 r/min.

maglev blower； brushless DC motor； sensorless； G function； closed-loop correction

2016-02-18

國家自然科學基金(61374029)；國家自然科學基金(61403015)

陳少華(1985—)，男，博士研究生，研究方向為高速大功率永磁電機控制； 劉 剛(1970—)，男，教授，博士生導師，研究方向為航天器姿態控制技術、精密機電控制系統； 鄭世強(1981—)，男，副教授，研究方向為航天器用磁懸浮慣性執行機構、高速磁懸浮電機技術； 郭金超(1990—)，男，碩士研究生，研究方向為高速大功率永磁電機控制。

陳少華

10.15938/j.emc.2017.04.015

TP 273

A

1007-449X(2017)04-0105-10