待測信號線性驅動Duffing振子弱信號檢測系統

盧 明，馬松山,2，丁家峰，黃 偉，袁 洪

待測信號線性驅動Duffing振子弱信號檢測系統

盧 明1，馬松山1,2，丁家峰1，黃 偉3，袁 洪3

(1.中南大學物理與電子學院，湖南長沙，410083；2.中南大學先進材料超微結構與超快過程研究所，湖南長沙，410083；3.中南大學湘雅三醫院，湖南長沙，410013)

針對周期驅動的Duffing振子微弱信號檢測系統存在臨界閾值影響信號檢測精度和對待檢測信號頻率分辨率不高的問題，提出一種以待檢測信號為驅動力的Duffing振子線性驅動弱信號檢測系統。該系統以待測信號作為系統線性驅動信號，利用系統線性驅動參數的微小變化會導致系統輸出狀態發生改變的特性，對淹沒在背景噪聲中的弱信號進行檢測。同時，通過計算系統的梅爾尼科夫函數和最大李氏指數，并結合系統相軌跡狀態的變化，對該系統檢測信號的可行性進行分析。研究結果表明：該檢測系統大大提高了對微弱信號頻率的分辨能力；檢測精度可達10?4，即諧波信號頻率與驅動力頻率之間的相對偏差ω-ω1/ω達10?4時依然可以檢測；增強系統對噪聲有免疫能力，同時可消除臨界閾值對系統檢測精度的影響，提高系統檢測效率。

Duffing振子；混沌；微弱信號檢測；頻率

混沌理論在弱信號檢測領域具有廣闊的應用前景，從而使其成為非線性科學中研究熱點，許多學者對其基本特點和實際應用進行了研究[1?5]。目前，利用混沌理論對信號的檢測主要體現在微弱信號的檢測方面，而基于Duffing混沌振子實現微弱信號的檢測是最典型的檢測系統[6?9]。由于Duffing混沌振子對信號初始值具有很強的敏感性，同時對噪聲具有很強免疫性，通過觀察體系相軌跡狀態的變化，即可實現微弱信號的檢測[10?11]。如范劍等[12]采用周期信號驅動的方式實現對Duffing狀態變化的控制，研究了Duffing振子檢測性能；WANG等[13]則研究了Duffing振子在強噪聲背景中進行信號檢測的基本原理及其可行性；李月等[14]研究了在噪聲背景下不同微弱方波信號激勵的Duffing振子檢測性能；鄧宏貴等[15]研究了采用小波去噪信號作為驅動力的改進型Duffing振子弱信號檢測方法，克服了對混沌臨界狀態與周期態區別的模糊性。這些針對Duffing系統微弱信號檢測的研究大都采用周期驅動的Duffing振子微弱信號檢測系統，而周期驅動信號檢測系統存在以下問題：1)該檢測系統由于混沌臨界閾值存在，檢測效率不高；2)該檢測系統的頻率分辨率不高，只有0.03[16]，當諧波噪聲頻率與驅動力頻率之間的相對偏差大于0.03時，系統無法免疫此類諧波噪聲，從而降低系統檢測精度。為此，本文作者提出一種以待測信號為驅動力，通過線性擾動方式來控制Duffing系統的狀態變化而實現弱信號檢測的Duffing振子弱信號檢測方法。在該方法中，用線性驅動的方式使Duffing系統狀態的變化得到更精確控制，通過設置新的系統測量參數，提高系統對噪聲的免疫程度，進一步改善系統檢測性能，消除臨界閾值對檢測系統影響。同時，對該檢測系統在不同頻率與幅值下的最大李雅普諾夫指數進行分析，并利用梅爾尼科夫函數分析系統狀態，研究系統相軌跡變化規律和系統的檢測性能。

1 線性驅動Duffing振子弱信號檢測模型

在周期驅動下，Duffing振子弱信號檢測模型可表示為[17?18]

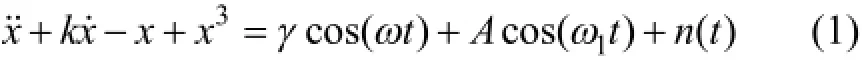
其中：k為阻尼系數；-x+ x3為非線性恢復力；γcos(ωt)為周期驅動信號項；γ為驅動信號幅值；ω為驅動信號頻率；Acos(ω1t)為待檢測信號項；A為待測信號幅值；ω1為待測信號頻率；n( t)為背景噪聲項。式(1)對應的狀態方程為

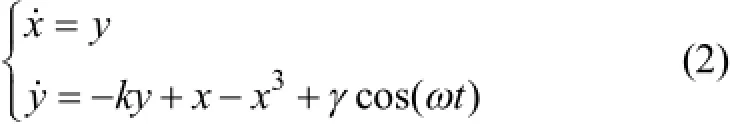
由(2)式可知：當0=γ時，系統的相平面為3個奇點，分別為鞍點(0,0)，焦點(1，0)和(?1，0)，且初始狀態不同，將導致點),(xx˙最終停在2個焦點之一。當γ較小時，系統的相軌跡表現為Poincare映射意義下的吸引子，相點將圍繞1個焦點或者另外1個焦點作周期運動。隨著γ增大，系統非線性部分影響增大，系統將進入同宿軌道狀態，如圖1(a)所示；進一步增大γ，系統將進入混沌狀態，如圖1(b)所示；但當γ增大到超過臨界閾值dγ時，系統非線性部分影響開始減弱，線性振子影響加強，系統將進入大周期狀態，如圖1(c)所示。

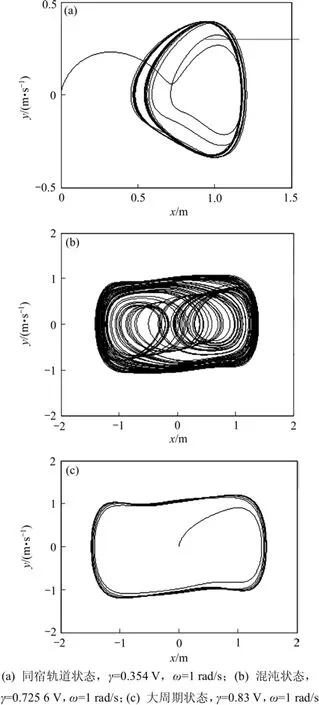
圖1 系統相軌跡狀態和時域狀態圖Fig.1 System trajectory state and time domain state

在進行信號檢測時，需將檢測系統設置為混沌臨界狀態。根據梅爾尼科夫指數[19]，周期信號驅動的混沌臨界閾值為由此可得周期信號驅動的混沌系統臨界閾值隨驅動信號頻率變化關系如圖2所示。由圖2可知：對于周期信號驅動的混沌系統來說，不同的驅動信號頻率對應不同的混沌系統臨界閾值，因此，當檢測不同頻率的信號時，需重新設置系統臨界閾值，這極大地降低了信號的檢測效率；另一方面，該檢測系統的頻率分辨力低于0.03，即ω-ω1/ω＞0.03，當諧波噪聲頻率與驅動力頻率之間的相對偏差大于0.03時，系統無法免疫此諧波噪聲，從而降低系統檢測精度。

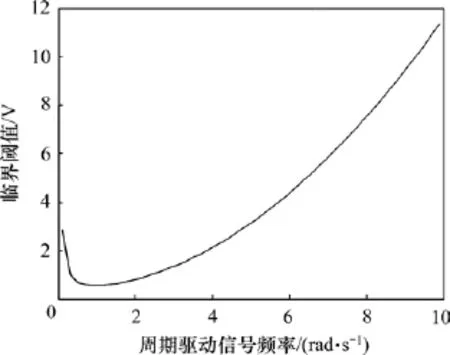
圖2 周期信號驅動Duffing系統臨界閾值與驅動信號頻率關系Fig.2 Relationship betw een chaos threshold of periodic driving force signalsand frequency

可見：對周期信號驅動的Duffing振子系統進行信號檢測時，系統對待檢測信號頻率敏感程度最低只能達到10?2[16]，且存在臨界閾值影響。因此，為提高對微弱信號頻率檢測的精度，根據混沌控制理論，構建基于待測信號線性驅動的Duffing混沌振子檢測系統，其Duffing方程可表示為

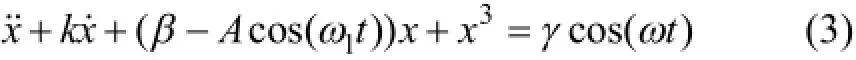
其中：β-Acos(ω1t )為輸入系統的待檢測信號項；ω1為待測信號頻率，其狀態方程為

為研究待測信號線性驅動Duffing振子弱信號檢測方法的可行性，利用梅爾尼科夫函數和不同頻率與幅值下的最大李雅普諾夫指數對其檢測原理進行分析。

2 線性驅動Du ffing振子弱信號檢測可行性分析

利用Duffing振子檢測信號時，系統能否在驅動信號影響下由混沌狀態進入大周期狀態是系統能否完成信號檢測的關鍵，由于梅爾尼科夫(Melnikov)通常用來區分系統是否進入混沌狀態，因此，利用梅爾尼科夫(Melnikov)對線性驅動的Duffing振子檢測系統狀態進行分析。當系統未受到擾動時，式(4)可以表示為Ham ilton系統：

該系統的Hamilton常量可表示為

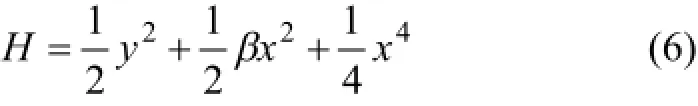
由式(5)可得系統的2個Hamilton軌道常量：

其中：0()x t和0()y t是系統2條同宿軌道的坐標參量，利用式(7)可求得系統的梅爾尼科夫函數，由此可知系統Melnikov函數為

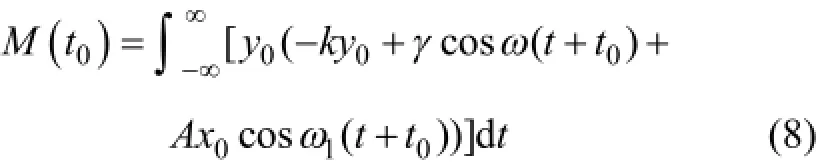
將式(7)代入式(8)，可得

根據Melnikov函數，若系統能進入混沌狀態，則式(9)將存在零解，也就是說，與式(3)相應的Poincare映射中，穩定不變行流與不穩定不變形流必然相交，即此時出現橫截同宿點，系統進入混沌狀態。因此，只需選擇合適的系統參數，線性驅動的Duffing振子能進入混沌狀態。

梅爾尼科夫函數存在零解只是系統進入混沌狀態的必要條件，因此，通過對該系統進行數據仿真，分析其最大李雅普諾夫指數，并結合系統梅爾尼科夫指數進一步分析系統所處狀態，判斷系統是否能在混沌狀態和大周期狀態之間轉換。

應當指出的是：只要式(9)有零解，Duffing振子微弱信號檢測系統即處于混沌狀態，因此，參量k和β等可以取不同值。為使問題簡化，設定系統參數為：k=0.5，1=β，3.0=γV，A=0.2V，ω=1 rad/s，并通過數值計算得到系統最大李雅普諾夫指數隨待測信號頻率之間的關系，如圖3所示。從圖3可見：只有當輸入待檢測信號的頻率ω1=ω或ω1=3ω時，系統的最大李氏指數小于0，分別為?0.004 97和?0.003 16，表明系統處于周期狀態。而當待檢測信號頻率為其他值時，系統最大李氏指數都大于0，系統仍處于混沌狀態。因此，隨著待測信信號頻率變化，系統可以實現混沌狀態與周期狀態轉變。

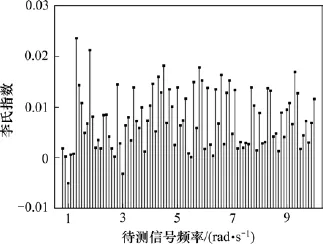
圖3 系統最大李氏指數與待檢測信號頻率關系Fig.3 Relationship between the largest Lyapunov index and themeasured signal frequency

為進一步研究系統對待測信號頻率的分辨精度，通過數值計算ω1=ω，ω1=1.000 1ω及ω1=0.999 9ω時系統的Melnikov函數，如圖4所示。從圖4(a)可知：當待測信號的頻率ω1=ω時，系統的Melnikov函數介于?2.0與?0.5之間，全部小于0，因此，式(9)不存在零解，說明系統此時已經進入周期狀態。而從圖4(b)和圖4(c)可知：當待檢測信號頻率分別取ω1=1.000 1ω和ω1=0.999 9ω時，系統的Melnikov函數介于?1.5與0.2之間，出現多個大于0的情況，式(9)存在多個零解，說明此時系統處于混沌狀態。

可見：通過待測信號線性驅動的方式可以實現系統由混沌狀態向大周期狀態轉變。因而在進行信號檢測時，只需將待檢測信號輸入Duffing振子檢測系統，通過調節信號頻率，當系統周期驅動力信號頻率ω與待檢測信號頻率ω1保持嚴格一致時，系統相軌跡狀態

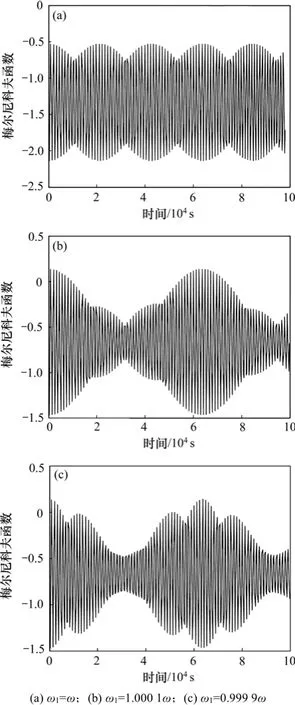
圖4 不同待測信號頻率下系統梅爾尼科夫函數值Fig.4 ValueofMelnikov function for different frequenciesof signals

將由混沌狀態進入大周期狀態，從而可完成信號檢測。

3 線性驅動Du ffing振子微弱信號檢測系統性能分析

由檢測原理可知，待測信號線性驅動Duffing振子系統具備弱信號檢測能力，下面進一步分析其檢測性能。考慮到噪聲的影響，此時Duffing振子方程可表示為

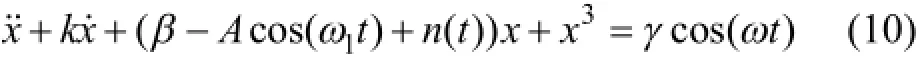
其中：()n t為高斯白噪聲信號項。

3.1 系統初始狀態對檢測效率的影響

從圖1可見：對于周期信號驅動的Duffing振子微弱信號檢測系統，系統從混沌狀態進入大尺度周期狀態時其相圖變化非常明顯，因此，該系統進行信號檢測時，必須將系統調整至混沌臨界狀態，也就是說，在周期信號驅動的Duffing振子微弱信號檢測系統中，待檢測信號的“混沌抑制力”必須在系統臨界狀態時才能體現。然而，目前混沌臨界閾值的確定主要通過觀察相位狀態的改變進行確定，因此，無法精確地對混沌臨界閾值進行確定，且由圖2可知，當系統驅動信號頻率不同時，系統臨界閾值亦不相同，這極大地降低了信號檢測效率。

利用待檢測信號線性驅動的Duffing振子微弱信號檢測系統進行信號檢測時，通過適當的系統參數設置，使系統處于混沌狀態。如前所述，取k=0.5，β=?1， γ=0.3V，ω=1 rad/s，此時系統處于混沌狀態，如圖5(a)所示。增大系統周期信號的幅值，如取γ=0.5V，此時系統狀態仍為混沌狀態，如圖5(b)所示。但在系統周期信號幅值保持不變即同樣取γ=0.3V時，一旦待檢測信號輸入檢測系統，系統由混沌狀態立即進入大周期狀態，如圖5(c)所示。通過進一步計算得到此時系統的最大李亞普若夫指數與待測信號幅值的關系，如圖5(d)所示。可知：當輸入系統的待檢測信號幅值逐漸增大時，系統的最大李雅普諾夫指數亦呈增大趨勢，但其值小于0，表明系統處于大周期狀態。也就是說，當輸入系統的待測信號幅值在較大范圍內變化時，系統依然能保持大周期狀態，可見在待檢測信號自驅動的Duffing振子混沌檢測系統中待檢測信號具有較強的“混沌抑制力”。因此，在實際檢測時，無需將系統調整至混沌臨界狀態，消除臨界閾值對檢測系統的影響，從而極大改善系統檢測性能，提高系統信號檢測能力。

3.2 檢測系統對噪聲“免疫”能力分析

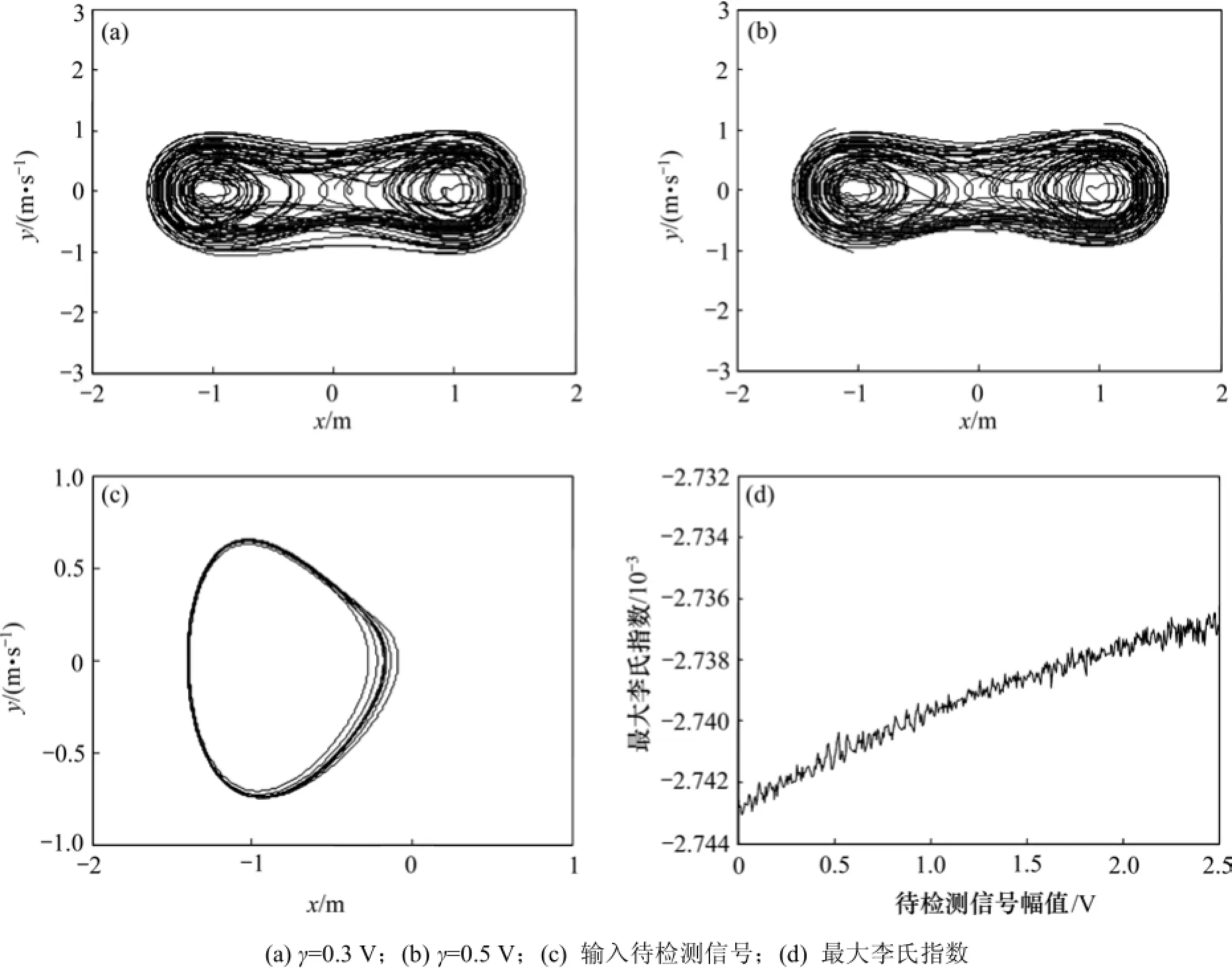
圖5 線性驅動Duffing系統的相軌跡Fig.5 Phase trajectoriesof linear drive Duffing system

對周期信號驅動的Du ffing系統進行信號檢測時，周期擾動信號與待檢測信號頻率的偏差應小于0.03[16]，即當待測信號頻率與周期擾動信號頻率的相對偏差小于0.03時，系統將由混沌狀態進入大周期狀態，從而完成信號檢測。但在信號檢測過程中，待測信號通常淹沒于系統噪聲和環境噪聲中，當噪聲頻率也與周期驅動信號頻率的偏差小于0.03時，系統無法分辨噪聲和待檢測信號，從而對檢測結果造成影響，產生檢測誤差。然而，對于待測信號線性驅動的Duffing振子信號檢測系統而言，當輸入系統的待檢測信號與系統頻率保持一致時，由圖4(a)可知，系統處于大周期狀態；但當待檢測信號頻率與系統頻率的偏差為0.000 1時(如圖4(b)和4(c)所示)，系統即可轉變為混沌狀態。可見：待測信號線性驅動的Duffing振子信號檢測系統的頻率分辨力可達0.000 1，這極大地提高了檢測系統的頻率分辨能力，檢測精度可達10?4數量級，即諧波信號頻率與驅動信號頻率之間的相對偏差ω-ω1/ω達10?4時依然可以進行檢測，從而有效地排除了諧波噪聲對檢測系統性能的影響。由此可知：線性擾動Duffing振子對噪聲具有更強的區分能力，能進一步提高信號檢測能力。在線性驅動的Duffing振子弱信號檢測系統中，該信號檢測系統擁有較強的頻率分辨能力和混沌抑制力，但利用該系統進行信號檢測時，對待檢測信號頻率精確度要求較高，且必須對信號頻率進行處理，這對系統檢測效率存在較大影響。

4 系統仿真結果與分析

4.1 系統仿真模型

為進一步檢測線性驅動Duffing振子系統的檢測性能，對其進行Matlab/Simulink仿真，仿真模型如圖6所示。設系統參數k=0.5，β=?1，γ=0.3V，ω=1 rad/s，通過仿真，可獲得不同信號頻率下系統的檢測結果，如表1所示。從表1可知：線性驅動Duffing弱信號檢測系統能有效完成信號頻率的檢測，提高頻率檢測分辨率，如當待檢測信號頻率為0.800 0 rad/s時，普通方法檢測結果為0.765 6 rad/s，相對誤差達4.3%，而采用待測信號線性驅動Duffing振子檢測系統進行檢測時，檢測結果為0.800 3 rad/s，相對誤差為0.003 7%，可知系統擾動系統具有更高的頻率分辨力。

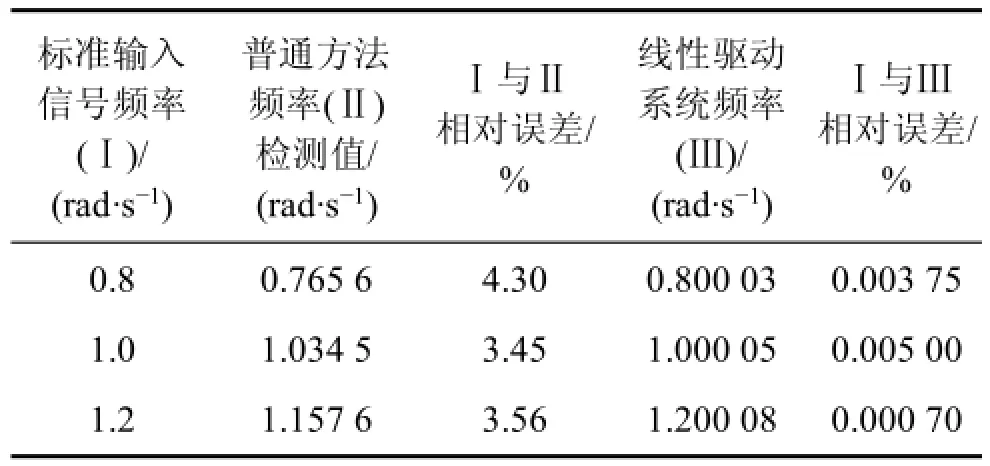
表1 不同頻率下系統檢測結果Table1 Detection resultsunder different frequencies

進一步研究待測信號線性驅動Duffing弱信號檢測系統對待測信號幅值檢測性能的影響，仿真結果如表2所示。從表2可知：當信噪比相同時，待檢測信號幅值越大，檢測時相對誤差越小，如當信噪比為?20 dB，待測信號理論幅值為0.01m V時，系統檢測到的幅值相對誤為4.7%，但當待測信號理論幅值為0.1m V時，系統檢測到的幅值相對誤差為3.9%。同時，輸入系統的待檢測信號信噪比越大，系統幅值檢測的相對誤差越小。可見，待測信號線性驅動Duffing振子檢測系統能有效完成對弱信號的檢測。

圖6 系統仿真模型Fig.6 Simulationmodelof the system

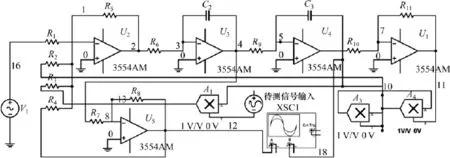
圖7 系統仿真電路圖Fig.7 Simulation circuitof system

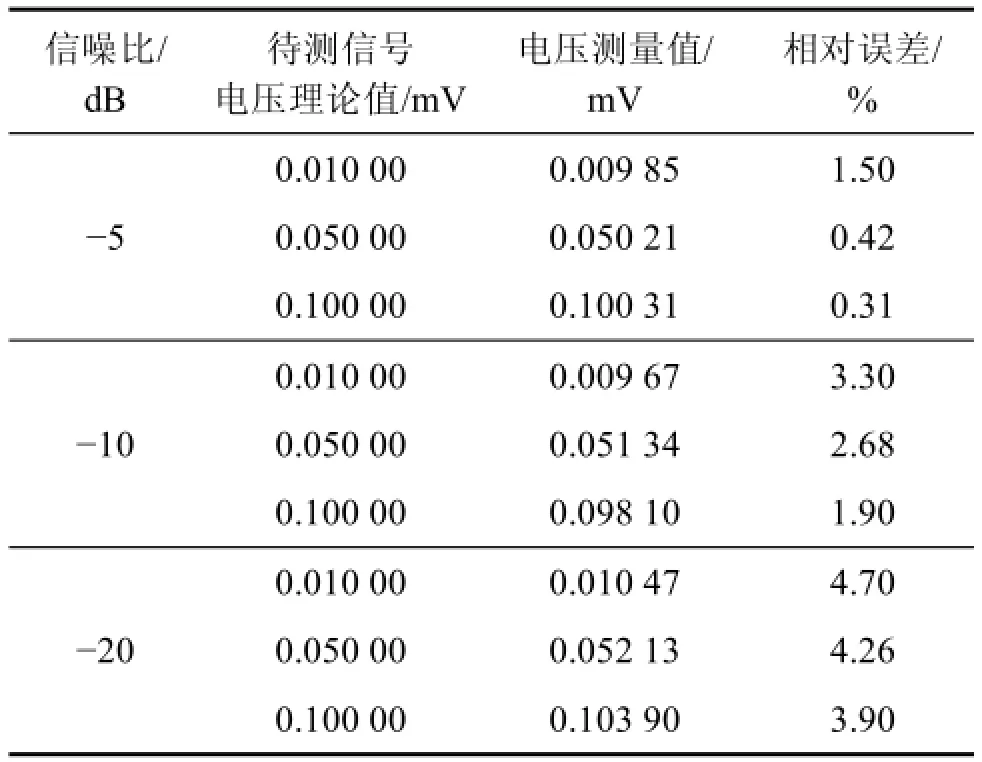
表2 線性驅動系統幅值檢測結果Table2 Am plitude detection resultsof system

4.2 系統仿真電路設計

利用Multisim軟件進一步對待檢測信號線性驅動的Duffing振子弱信號檢測系統的電路進行設計。在系統參數設定為k=0.5，β=?1的情況下，式(4)可改寫為

與(11)式對應的電路狀態方程為

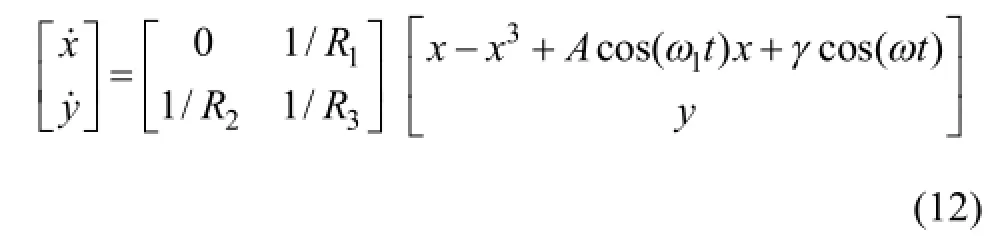
根據式(12)，可得到其電路圖，如圖7所示。在此電路中，選定電阻R3=2R1=2R2，C1=C2。利用該仿真電路，可先將電路調制在混沌狀態，然后將待檢測信號加入檢測系統，可以發現系統將由混沌狀態進入周期狀態，證明該仿真電路系統能很好地實現弱信號檢測。

5 結論

1)提出了待測信號線性驅動Duffing振子微弱信號檢測系統。系統的梅爾尼科夫函數和最大李雅普諾夫指數及仿真結果表明待測信號線性驅動Duffing振子微弱信號檢測系統能很好地實現弱信號的檢測。

2)待測信號線性驅動Duffing振子微弱信號檢測系統能大大提高系統對待檢測信號的頻率分辨力，其頻率檢測精度可達10?4，從而提升系統噪聲免疫能力。

3)待測信號線性驅動Duffing振子微弱信號檢測系統能有效地消除在周期信號驅動Duffing振子檢測系統中的臨界閾值的影響，提高系統檢測效率，實現較強噪聲背景下的微弱周期信號檢測。

[1]DENG Xiaoying,LIU Haibo,LONG Teng.A new complex Duffing oscillator used in complex signal detection[J].Chin Sci Bull,2012,57(17):2185?2191.

[2]RASHTCHI V,NOURAZAR M.A multiprocessor ions II imp lementation of Duffing oscillator array for weak signal detection[J].Journal of Circuits Systems and Computers,2014, 23(4):1450054.

[3]CHANG Yuan,HAO Yi,LI Chunwen.Phase dependent and independent frequency identification of weak signals based on Duffing oscillator via particle swarm optim ization[J].Circuits Systems And Signal Processing,2014(1):223?239.

[4]胡方靜.用于金屬探測的混沌振子系統研究[D].濟南:山東大學電氣工程學院,2012:20?43.

HU Fangjing.Study of chaotic oscillator formetal detection[D]. Jinan:Shandong University.School of Electrical Engineering, 2012:20?43.

[5]魏恒東.混沌直擴信號檢測與混沌同步研究[D].成都:電子科技大學電子工程學院,2010:4?32.

WEI Hengdong.A study on the detection of chaotic direct sequence spread spectrum signal and chaos synchronization[D]. Chengdu:School of Electronic Engineering,University of Electronic Science and Technology of China,2010:4?32.

[6]RASHTCHIV.Detecting the state of the Duffing oscillator by phase space trajectory auto-correlation[J].International Journal of Bifurcation and Chaos,2013,23(4):1350065.

[7]RASHTCHI V,NOURAZAR M,AGHMASHEH R.Fault diagnosis of broken bars in squirrel cage inductionmotors using Duffing oscillators[J].International Review of Electrical Engineering,2012,7(3):4457?4468.

[8]JIN Tian,ZHANG Hua.Statistical approach to weak signal detection and estimation using Duffing chaotic oscillators[J]. ScienceChina:Information Sciences,2011,54(11):2324?2337.

[9]蔣芳芳.體震信息監測系統中的微弱信號檢測與分析方法研究[D].沈陽:東北大學信息科學與工程學院,2011:42?55.

JIANG Fangfang.Research on weak signal detection and analysis approach in the ballistocardiogram information Monitoring system[D].Shenyang:Northeastern University. Collegeof Information Science and Engineering,2011:42?55.

[10]汪金山,汪曉東,施曉鐘.基于Duffing混沌系統微弱信號檢測的數值分析[J].儀器儀表學報,2005,26(8):33?34.

WANG Jinshan,WANG Xiaodong,SHI Xiaozhong,et al. Numerical analysis for weak signal detection based on Duffing chaotic system[J].Chinese Journalof Scientific Instrument,2005, 26(8):33?34.

[11]LEUNG H,HUANG Xingping.Sinusoidal frequency estimation in chaotic noise[J].International Conference on Acoustics, Speech,and Signal Processing,1995,3(2):1344?1347.

[12]范劍,趙文禮,王萬強,等.基于Duffing振子的微弱周期信號混沌檢測性能研究[J].物理學報,2013,62(18): 180502-1?180502-6.

FAN Jian,ZHAOWenli,WANGWanqiang,et al.Study on the weak sinusoidal signal detection property using Duffing chaos system[J].Acta Physica Sinica,2013,62(18):180502-1?180502-6.

[13]WANG Guanyu,HE Sailing.A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators[J].IEEE Transactions on Circuits and Systems I: Fundamental Theory and App lications,2003,50(7):945?953.

[14]李月,石要武,馬海濤,等.湮沒在色噪聲背景下微弱方波信號的混沌檢測方法[J].電子學報,2004,32(1):87?90.

LIYue,SHIYaowu,MA Haitao,etal.Chaotic detectionmethod for weak squarewave signal submerged in colored noise[J].Acta Electronica Sinica,2014,32(1):87?90.

[15]鄧宏貴,曹文暉,楊兵初,等.基于混沌理論和小波變換的微弱周期信號檢測方法[J].中南大學學報(自然科學版),2012, 43(5):1773?1779.

DENG Honggui,CAO Wenhui,YANG Bingchu,et al.Weak periodical signal detection based on wavelet threshold de-noising and chaos theory[J].Journal of Central South University (Science and Technology),2012,43(5):1773?1779.

[16]馮進鈐,徐偉,牛玉俊,等.Duffing單邊碰撞系統的顫振分岔[J].物理學報,2010,59(1):157?163.

FENG Jinqian,XUWei,NIU Yujun.Chattering bifurcations in a Duffing unilateral vibro-impact system[J].Acta Physica Sinica, 2010,59(1):157?163.

[17]李月,路鵬,楊寶俊,等.用一類特定的雙耦合Duffing振子系統檢測強色噪聲背景中的周期信號[J].物理學報,2006, 55(4):1672?1677.

LIYue,LU Peng,YANG Baojun.Applying a special kind of two coupled Duffing oscillator system to detect periodic signals under the background of strong colored noise[J].Acta Physica Sinica,2006,55(4):1672?1677.

[18]SHISihong,YUAN Yong,WANG Huiqi.Weak signal frequency detection method based on generalized Duffing oscillator[J]. Chinese Physics Letters,2011,28(4):040502.

[19]李月,祁放,張銘,等.微弱正弦信號的一種新的混沌檢測系統[J].儀器儀表學報,2004,25(Z1):19?20.

LIYue,QI Fang,ZHANG M ing.The detection of weak sine signals using special chaotic system[J].Chinese Journal of Scientific Instrument,2004,25(Z1):19?20.

(編輯 陳燦華)

W eak signaldetection system based on
Duffing oscillator w ith linear driven by to-be-detected signal

LUM ing1,MA Songshan1,2,DING Jiafeng1,HUANGWei3,YUAN Hong3

(1.School of Physics and Electronics,Central South University,Changsha410083,China; 2.Institute of Super-m icrostructure and Ultrafast Process in Advanced M aterials,Central South University, Changsha 410083,China; 3.The third X iangya Hospital,Central South University,Changsha 410083,China)

Considering that the weak signal detection methods based on Duffing oscillator w ith periodic driving force signal have the defects that the detection accuracy can be affected by the critical threshold and the frequency resolution is nothigh enough,a new weak signal detectionmethodwas presented based on Duffing oscillator,which wasdriven by the linear perturbation of the to-be-detected signal.In the method,the small change of the linear perturbation parameters could cause the output change,and then this characteristic could be used to detect the w eak signals submerged in the background noise.Meanwhile,based on the Melnikov function and themaximum of Lyapunov exponent,the feasibility of the detection system was analyzed.The results show that themethod can greatly improve the frequency resolution of weak signal,and the precision of the frequency achieves 10?4.It can also enhance the noise immunity ability and elim inate the effectof critical threshold on the precision of the system.

Duffing oscillator,chaos;weak signal detection;frequency

TN911.7

A

1672?7207(2017)03?0721?08

10.11817/j.issn.1672-7207.2017.03.021

2016?03?21；

2016?05?25

國家自然科學基金資助項目(61172047,11204263)；湖南省科研條件創新專項(2011TT1009)(Projects(6172047,11204263) supported by the National Natural Science Foundation of China;Project(2011TT1009)supported by the Special Funds of Scientific Research Innovation of Hunan Province)

馬松山，副教授，從事微弱信號處理研究；E-mail:songshan@csu.edu.cn