有領導者線性多智能體系統一致性的分析與設計

蓋彥榮，陳陽舟，宋學君，齊耀輝

有領導者線性多智能體系統一致性的分析與設計

蓋彥榮1，陳陽舟2，宋學君1，齊耀輝1

(1.河北師范大學物理科學與信息工程學院，河北石家莊，050024；2.北京工業大學城市交通學院，北京，100124)

研究有向信息拓撲下有領導者線性多智能體系統的一致性分析與設計問題。利用提出的線性變換，將領導者有擾動輸入的多智能體系統一致性問題轉換為輸入到狀態穩定性問題。得到有向信息拓撲下有領導者線性多智能體系統達到一致的基于矩陣Hurw itz穩定的判據和誤差估計函數，同時設計反饋增益矩陣，并將有領導者多智能體系統的一致性問題擴展到編隊控制問題。數值實例驗證表明：所得理論具有有效性。

多智能體系統；有領導者一致性；輸入到狀態穩定性；一致性判據；編隊控制

多智能體系統的一致性問題是多智能體系統協作控制中的典型問題之一，受到了眾多領域學者的廣泛關注[1]。文獻[1?6]研究了無領導者多智能體系統的一致性問題，其一致函數是所有智能體初始狀態的加權平均值或加權冪平均值。但是當要求所有智能體達到一個指定的一致函數時，則需要研究有領導者的多智能體系統的一致性問題[7?14]。領導者作為特殊的智能體，其行為獨立于其他的智能體；而其他智能體跟隨該領導者，最終達到領導者確定的一致函數。文獻[7]研究了一階多智能體系統跟蹤時變一致參考狀態的問題，考慮了控制能力有界和有向切換信息拓撲下只有部分智能體可以獲得參考狀態的情況；文獻[8，11]研究了有領導者一階和二階多智能體系統在領導者信息不可測量情況下的一致性問題；文獻[15?17]對有領導者不同系統動態的高階多智能體系統的一致性進行了研究。在分布式協作控制系統中，智能體多為高階系統，而且領導者的運動狀態在實際運行中難免會受到干擾。因此在領導者存在擾動輸入的情況下，設計跟隨者智能體的控制協議，在允許的有界范圍內達到多智能體系統的一致是一個值得研究的問題。本文作者利用適當的線性變換[6]，將有向信息拓撲下領導者有擾動輸入的有領導者線性多智能體系統(leaderfollow ing linearmulti-agent systems，LLMASs)的一致問題轉換為相應系統的輸入到狀態穩定問題。利用輸入到狀態穩定理論[18?19]，得到有向信息拓撲下LLMASs一致性判據。同時設計反饋增益矩陣，使得LLMASs達到輸入到狀態穩定一致。與已有文獻相比，本文具有以下優點：第一，提出的線性變換矩陣構造簡單，推理過程簡潔易懂；第二，利用該線性變換，將領導者有擾動輸入的多智能體系統一致性問題轉換為相應系統的輸入到狀態穩定性問題，得到的一致性判據更容易驗證，只需要判斷一個實數矩陣的Hurwitz穩定性即可；第三，利用Riccati方程，設計反饋增益矩陣，使得給定有向信息拓撲下有領導者多智能體系統達到輸入到狀態穩定一致；第四，將領導者輸入有擾動的LLMASs一致性問題的研究成果應用于多智能體系統編隊控制。

1 問題描述

為便于描述，給出如下定義：Rn和Rn×m分別表示n維實數向量和n×m維的實數矩陣；I和0分別表示合適維數的單位矩陣和零矩陣；1N表示所有元素為1的列向量；?表示矩陣或向量的Kronecker積[20]，Kronecker積有2個性質：

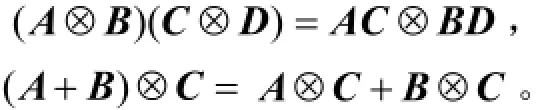
考慮N個智能體構成的LLMASs，第1個智能體為領導者，其他智能體為跟隨者，系統動態方程為:

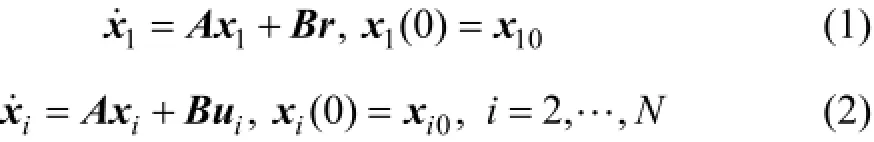
其中：xi∈ Rn和ui∈ Rm分別為系統的狀態變量和控制輸入變量；r∈ Rm為第1個智能體的擾動輸入變量，是滿足||r||∞≤δ(|| r||∞=supt≥0|| r( t )||,δ∈ R)的光滑有界函數；A和B是合適維數的矩陣。

控制輸入 ui的建立基于智能體i可以得到的信息，令Ni表示可以發送信息給智能體i的鄰居智能體集合。我們稱NT={ Ni: i=1,…, N}為LLMASs(1)和(2)的信息拓撲。眾所周知，可以用有向加權圖G=( V, E,W)來表示信息拓撲 NT，其中頂點V={1,…, N}是N個智能體的集合，E? V× V描述智能體間信息交互的有向邊集，即(j, i)∈ E? j∈ Ni。基于有向邊集可以構建與信息拓撲相關聯的權值矩陣W=[wij]N×N。當j= i時，元素wij=0，當i≠ j時，若j∈ Ni，則wij≥0；若j? Ni，則wij=0。相應的加權入度矩陣和加權圖Laplacian矩陣分別定義為Dw=diag{d1,…, dN}和Lw= Dw- W，其中di=是頂點i的入度。本文信息拓撲可以描述為以領導者1為根節點的有向圖。

假定領導者的擾動輸入r可以在線測量，則給定有向信息拓撲 NT下跟隨者的控制協議為

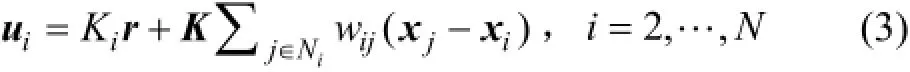
其中：K為反饋增益矩陣；Ki描述智能體i能否在線直接測量領導者的擾動輸入r，若1iN∈，則Ki＞0；否則Ki=0。

LLMASs(1)和(2)在協議(3)下的矢量形式如下：

定義1給定有向信息拓撲 NT，若系統(4)存在KL類函數β:R+× R+→ R和K類函數γ:R+→ R使得式(5)成立，

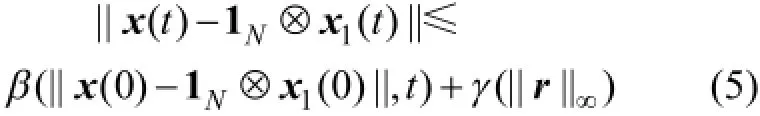
則稱LLMASs(1)和(2)在協議(3)下可達到輸入到狀態穩定一致。若γ(||r||∞)=0，則稱LLMASs(1)和(2)在協議(3)下可達到(嚴格)一致。

2 輸入到狀態穩定一致性分析

下面分析LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致問題。首先利用選取的線性變換，等價地將有領導者多智能體系統的一致性問題轉換為相應線性系統的輸入到狀態穩定性問題；然后依據穩定性理論，得到LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致的判據。

2.1 問題轉換

根據文獻[6]中線性變換的思想，為了簡單起見，選取的線性變換矩陣T為

相應的逆矩陣1-T為

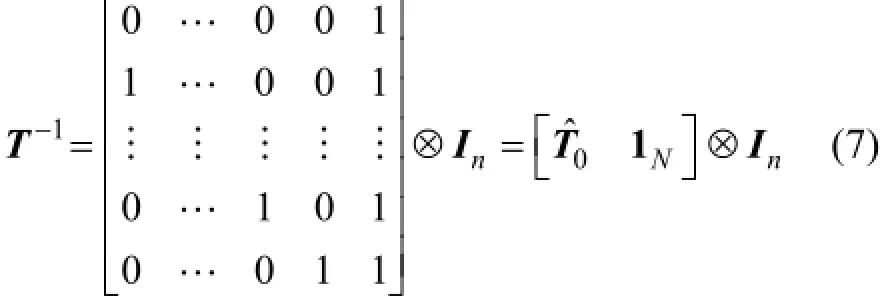
利用線性變換矩陣(6)對系統(4)進行線性變換

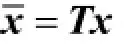
得到下面形式的線性系統

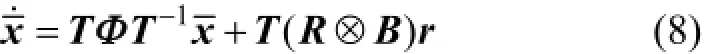
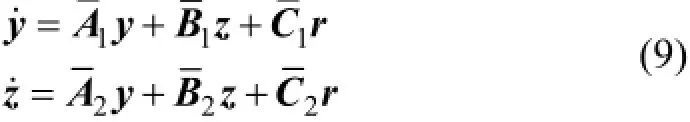
其中：

引理1線性系統(9)具有下面的形式

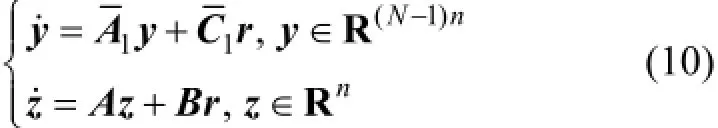
其中：

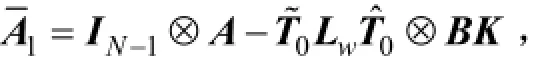
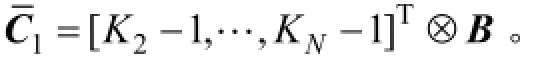
證明：由于線性變換矩陣T和圖Laplacian矩陣滿足3個條件：

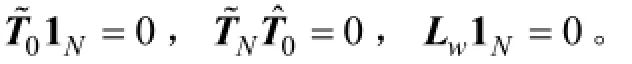
利用這3個條件和Kronecker積的2個常用性質，得到線性系統(9)中的系數矩陣分別為因此系統(9)具有系統(10)的形式。

2.2 一致性判據

引理2 LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致的充分條件是系統(10)的平衡點y=0∈ R(N-1)n是李亞普諾夫意義下輸入到狀態穩定的。

證明：假設系統(10)的平衡點y=0是李亞普諾夫意義下輸入到狀態穩定的，即存在KL類函數β和K類函數γ，使得||y(t)||≤β(|| y(0)||,t)+γ(|| r ||∞)成立。由線性變換x= Tx得到xi= xi+1- x1，i=1,2,…, N-1。因此，如果平衡點y=0為李亞普諾夫意義下輸入到狀態穩定的，可以得到系統(4)滿足式(5)，即LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致。

綜合引理1和引理2，得到如下定理。

定理1給定有向信息拓撲 NT，LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致的條件是系統(10a)的系數矩陣A1是Hurw itz穩定的。同時，如果矩陣A1是Hurwitz穩定的，對于給定正數c和σ，多智能體系統的跟蹤誤差由下面的不等式確定

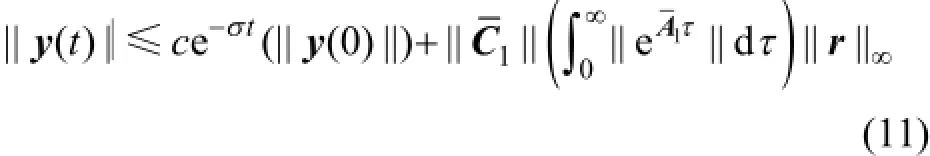
其中：

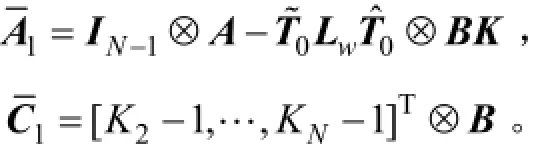
證明：根據引理1和引理2，得到LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致等價于系統(10)的輸入到狀態穩定，而系統(10)的輸入到狀態穩定可以通過系數矩陣A1的Hurwitz穩定得到。同時，根據輸入到狀態穩定性理論[19]，系統達到輸入到狀態穩定一致的跟蹤誤差由不等式(11)確定。

通過把矩陣A1轉換為其約當標準型，可以得到下面的定理：

定理2給定信息拓撲 NT，LLMASs(1)和(2)在協議(3)下達到輸入到狀態穩定一致的條件是N-1個矩陣A-λiBK是Hurw itz穩定的，其中λi是矩陣T~0LwT?0的N-1個特征值。如果N-1個矩陣A-λiBK是Hurwitz穩定的，對于給定正數c和σ，多智能體系統的跟蹤誤差由不等式(11)確定。

注1：矩陣T~0LwT?0的N-1個特征值為矩陣 Lw的N-1個非零特征值。

注2：若領導者的擾動項r不可直接測量，則設計跟隨者的控制協議為

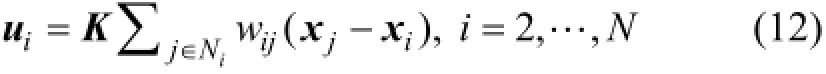
利用同樣的變換方法，LLMASs(1)和(2)在協議(12)下可以得到形如式(10)的系統，其中于是得到下面的推論。

推論1給定有向信息拓撲 NT，LLMASs(1)和(2)在協議(12)下達到輸入到狀態穩定一致的條件是線性系統(10a)的矩陣A1是Hurw itz穩定的；如果矩陣A1是Hurwitz穩定的，對于給定正數c和σ，多智能體系統的跟蹤誤差由不等式(11)確定。其中A1= IN-1? A- T~0LwT?0? BK，C1=[-1,…,-1]T?B。

推論2若領導者為確定系統，即r≡0，則給定有向信息拓撲 NT，LLMASs(1)和(2)在協議(3)或(12)下達到(嚴格)一致當且僅當線性系統(10)的矩陣A1是Hurwitz穩定的，且一致函數為ξ(t)=x1( t)。

3 反饋增益矩陣設計

根據定理2得到，矩陣A1是Hurwitz穩定的，等價于所有矩陣A-λiBK是Hurwitz穩定的，其中λi, i=1,…, N -1，是矩陣的N-1個特征值。當給定系統動態和信息拓撲后，只需設計反饋增益矩陣K，確保有領導者多智能體系統達到輸入到狀態穩定一致。受到文獻[5]的啟發，得到下面的定理。

定理3假定(A, B)可鎮定，給定的有向信息拓撲 NT使得具有N-1個特征值-λi的矩陣-T~0LwT?0是Hurwitz穩定的，其中：i=1,…, N-1，那么反饋增益矩陣K=λ-1( BTP)可以確保LLMASs(1)和(2)在協議

min

(3)下達到輸入到狀態穩定一致，其中λmin= min(Re(λi))，PT= P≥ 0是下面Riccati方程的解。

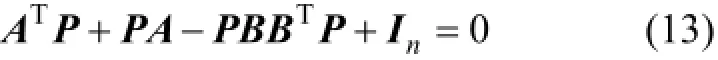
證明：由于信息拓撲 NT是連通的，即矩陣T~0LwT?0的N-1個特征值λi都在復平面的右半平面，亦即Re(λi)＞0，i=1,…, N-1。令λmin= min(Re(λi))，可以得到λmin＞0。考慮下面的系統

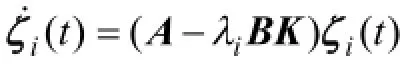
構建如下的Lyapunov候選函數

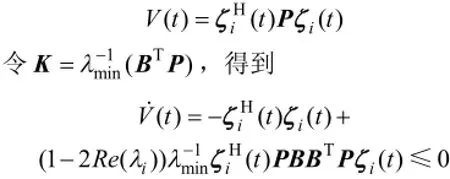
即N-1個矩陣A-λiBK都是Hurw itz穩定的，所以LLMASs(1)和(2)在協議(3)下可以達到輸入到狀態穩定一致。

根據定理3，可以得到反饋增益矩陣K的算法，具體設計步驟如下：

步驟1)判斷(A, B)的可鎮定性和信息拓撲的連通性。若2個條件中的任一個不成立，則算法終止；

步驟2)求解Riccati方程(13)，得到矩陣P；

步驟3)求得λmin= min{Re(λi)}；

4 編隊控制

在給定信息拓撲 NT下，以領導者為參照物，使得多智能體系統達到期望的隊形h=。

構建跟隨者分布式編隊控制協議為

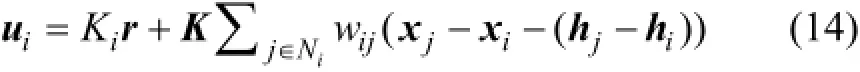
需要指出的是：當hj- hi=0，編隊控制協議(14)變為一致性控制協議(3)。

定義2給定信息拓撲 NT，若存在KL類函數β:R+× R+→ R和K類函數γ:R+→ R使得下式成立，則稱LLMASs(1)和(2)在協議(14)下可達到輸入到狀態穩定編隊。

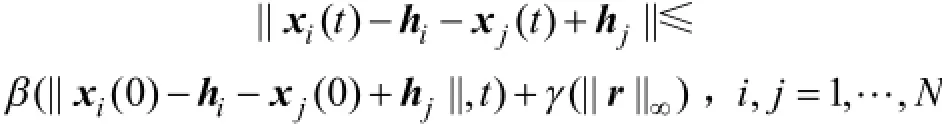
定理4給定信息拓撲 NT，LLMASs(1)和(2)在協議(14)下達到期望隊形h，當且僅當線性系統(10)的A1是Hurw itz穩定的，且對于給定正數c和σ，多智能體系統的編隊誤差由不等式(11)確定。

證明當r=0時，令x~i= xi- hi，LLMASs(1)和(2)可以達到期望隊形h當且僅當limt→∞x~i(t)- x~j( t)=0。

LLMASs(1)和(2)變為

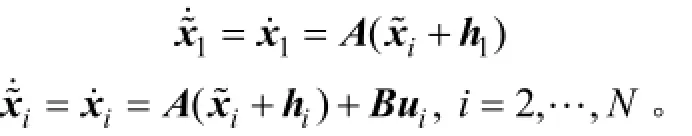
LLMASs(1)和(2)的向量形式表示如下：

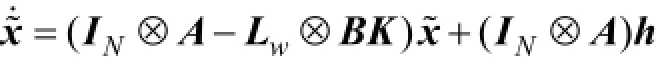
對上式進行線性變換x= Tx~，得到

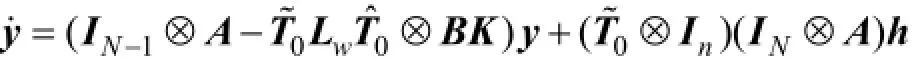
因為y=0一定是平衡點，所以有(T~0? A) h=0。且狀態參考一致函數為ξ(t)=x1( t)。

當r≠0時，可參照定理1的方法來證明LLMASs(1)和(2)在協議(14)下達到輸入到狀態穩定編隊。

類比于多智能體系統的一致性問題的研究，得到下面關于多智能體系統編隊控制的推論。

推論3給定通信拓撲 NT，LLMASs(1)和(2)在協議(14)下達到期望隊形h，當且僅當所有矩陣A-λiBK是Hurw itz穩定的，而且(T~0? A) h=0，其中λi是矩陣的特征值，i=1,…, N-1。

注3：注意到LLMASs(1)和(2)在協議(14)下不是所有隊形都可達的，可達的隊形必須滿足約束條件(T~0? A) h=0。

注4：對于給定的可達隊形，協議(14)中反饋增益矩陣可以利用第3節的算法進行設計。

5 數值實例

本節選用2個數值實例分別驗證有領導者線性多智能體系統在有向信息拓撲下的輸入到狀態穩定一致問題和編隊控制問題。

5.1 輸入到狀態穩定一致實例

假定LLMASs包含6個智能體，其中第1個智能體為領導者，則LLMASs的動態為

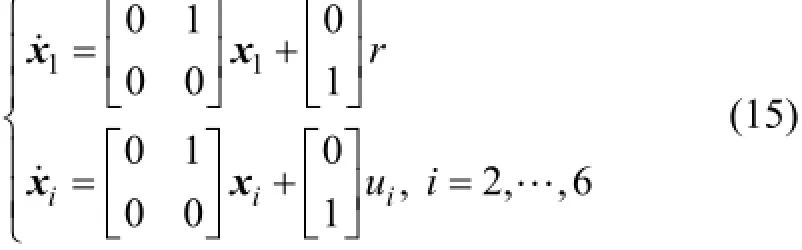
信息拓撲如圖1所示。

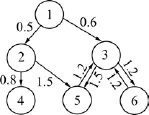
圖1 信息拓撲Fig.1 Information topology

信息拓撲對應的加權圖Laplacian矩陣為

經檢驗，(A，B)是可鎮定的，且信息拓撲是連通的。根據反饋增益矩陣設計算法，得到系統的反饋增益矩陣K=[3.289 6 2.788 8]。由于在給定的信息拓撲和設計的反饋增益矩陣下，系統(10)的系數矩陣A1是Hurwitz穩定的。根據定理1得到LLMASs(15)在給定信息拓撲(圖1)和一致性控制協議(3)下可以達到輸入到狀態穩定一致。

情形1)r可測量時，

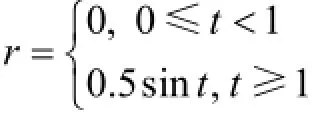
假定所有智能體起始于相同的初始狀態xi1(0)=1，xi2(0)=4。LLMASs(15)在控制協議(3)和圖1所示信息拓撲下的狀態誤差軌跡如圖2所示。狀態誤差分別為yi1= xi1- x11，yi2= xi2- x12，其中i=1,…,6。從圖2可以看出：LLMASs(15)達到輸入到狀態穩定一致，且狀態誤差是有界的。

情形2)r不可測量時，

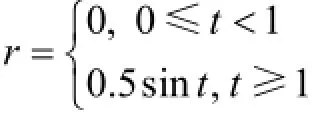
所有智能體的初始狀態同情形1)，LLMASs(15)在協議(12)和圖1所示信息拓撲下的狀態誤差軌跡如圖3所示，其中狀態誤差的定義同情形1)。從圖3可以看出：跟隨者和領導者的誤差在一定范圍之內，即輸入有界，系統狀態也有界。所以LLMASs(15)在給定圖1信息拓撲和不可測量擾動輸入下，達到輸入到狀態穩定一致。

圖2 多智能體系統在情形1)下的狀態誤差軌跡Fig.2 Error trajectoriesof LLMASs under situation 1)

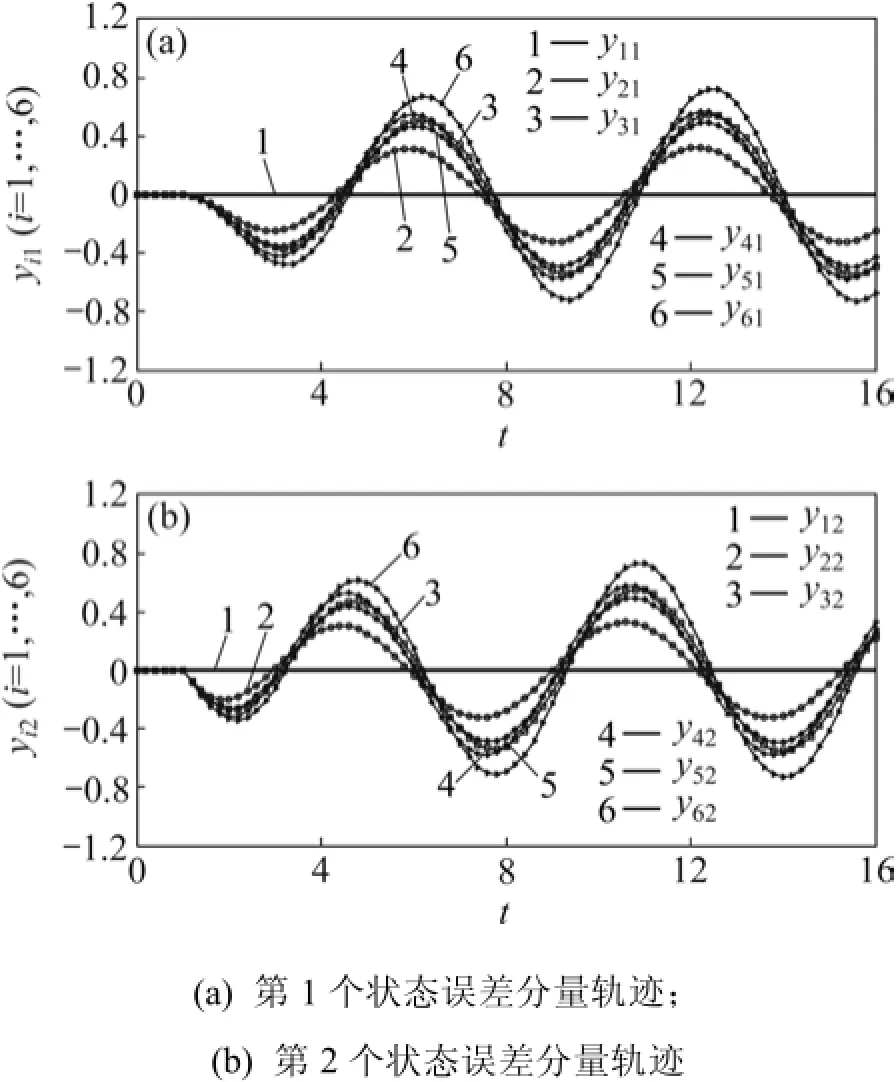
圖3 多智能體系統在情形2)下的狀態誤差軌跡Fig.3 Error trajectoriesof LLMASs under situation 2)

5.2 編隊控制實例

LLMASs包含4個智能體，其中第1個智能體為領導者，多智能體系統的動態為

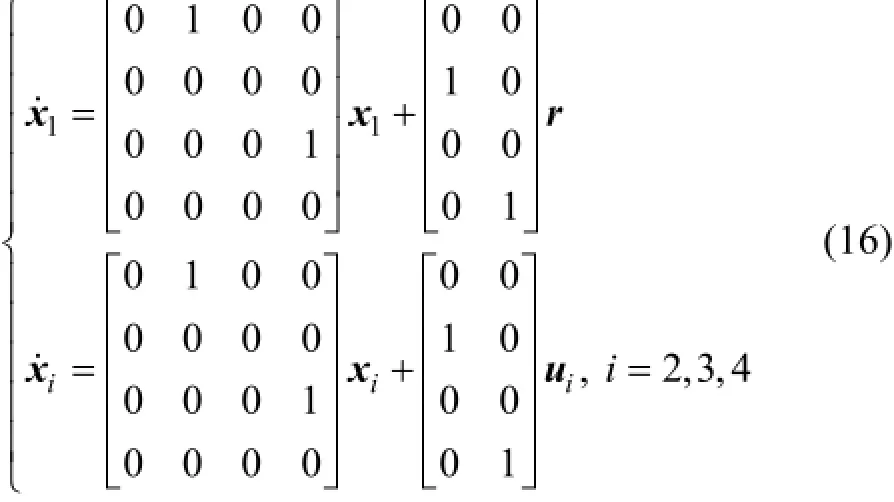
系統的信息拓撲為NT={?,{1},{2},{3}}，當智能體間有信息傳遞時，權值為0.5，否則權值為0。多智能體系統的期望隊形h為h1=[0,0,0,0]T，h2=[?3,0,0,0]T，h3=[?3,0,?3,0]T，h4=[0,0,?3,0]T。

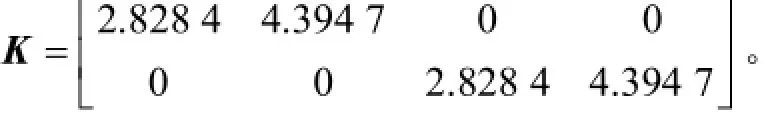
經檢驗，矩陣A1是Hurwitz穩定的。根據定理4，在給定的信息拓撲和權值矩陣以及增益矩陣K下，LLMASs(16)利用協議(14)可以達到期望隊形h。給定領導者的擾動輸入為r=[0.5sin t, 0. 5sin t]T，多智能體系統的初始狀態x1(0)=[9,2.4,18,1.8]T，x2(0)= [3,1.8,27,0.9]T，x3(0)=[3,1.2,6,?1.5]T，x4(0)= [4.5,1.8,24,?1.2]T，得到多智能體系統的編隊演化軌跡，如圖4所示，圖中“×”代表初始位置，“○”代表t=12 s時的位置。從圖4可以看到：LLMASs(16)在編隊控制協議(14)和給定信息拓撲及設計的反饋增益矩陣下達到期望隊形。

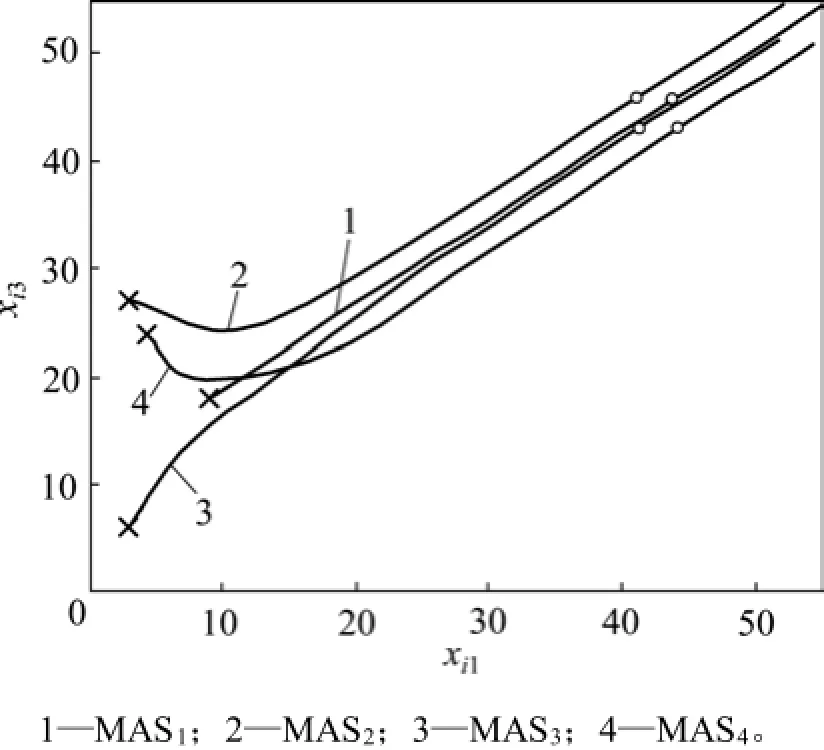
圖4 多智能體系統的編隊軌跡Fig.4 Formation trajectoriesof LLMASs

6 結論

1)主要研究領導者有擾動輸入情況下有領導者線性多智能體系統的一致性問題。首先定義了有領導者多智能體系統的輸入到狀態穩定一致；然后通過合適的線性變換，把有領導者的多智能體系統輸入到狀態穩定一致問題轉化為相應線性系統的輸入到狀態穩定問題，從而得到了給定有向信息拓撲下有領導者線性多智能體系統達到輸入到狀態穩定一致的基于矩陣Hurwitz穩定的判據；同時利用Riccati方程，設計了反饋增益矩陣，使得給定信息拓撲下有領導者多智能體系統達到輸入到狀態穩定一致；進而研究了多智能體系統的編隊控制問題。

2)實際情況下，由于傳感器的檢測范圍受限或存在障礙物，使得通信鏈路斷開或重連，由此導致信息拓撲結構發生變化；而且在網絡環境下，通信時延是很普遍的現象。本文只是研究了固定信息拓撲下有領導者線性多智能體系統的一致性問題，復雜通信情況下的拓展研究將是下一步的研究目標。

[1]OLFATI-SABERR,FAX JA,MURRAY R M.Consensus and cooperation in networked multi-agent systems[J].Proceedings of the IEEE,2007,95(1):215?233.

[2]SUN Yuangong,WANG Long,XIE Guangm ing.Average consensus in networks of dynam ic agents w ith sw itching topologies and multip le time-varying delays[J].Systems& Control Letters,2008,57(2):175?183.

[3]譚拂曉,關新平,劉德榮.非平衡拓撲結構的多智能體網絡系統一致性協議[J].控制理論與應用,2009,26(10): 1087?1092.

TAN Fuxiao,GUAN Xinping,LIU Derong.Consensus protocol in networkedmulti-agent systemsw ith non-balanced topology[J]. Control Theory&Applications,2009,26(10):1087?1092.

[4]XIJianxiang,CAINing,ZHONG Yisheng.Consensus problems for high-order linear time-invariant swarm systems[J].Physica A: Statistical M echanics and its Applications,2010,389(24): 5619?5627.

[5]MA Cuiqin,ZHANG Jifeng.Necessary and sufficient conditions for consensusability of linear multi-agent systems[J].IEEE Transactionson Automatic Control,2010,55(5):1263?1268.

[6]CHEN Yangzhou,GE Yanrong,ZHANG Yaxiao.Partial stability approach to consensus problem of linear multi-agent systems[J].Acta Automatica Sinica,2014,40(11):2573?2584.

[7]REN W ei.Consensus tracking under directed interaction topologies:algorithmsand experiments[J].IEEE Transactions on Control Systems Technology,2010,18(1):230?237.

[8]HONG Yiguang,HU Jiangping,GAO Linxin.Tracking control for multi-agent consensus with an active leader and variable topology[J].Automatica,2006,42(7):1177?1182.

[9]PENG Ke,YANG Yupu.Leader-follow ing consensus problem w ith a varying-velocity leader and time-varying delays[J]. Physica A:Statistical Mechanics and its Applications,2009, 388(2/3):193?208.

[10]MA Cuiqin,LI Tao,ZHANG Jifeng.Consensus control for leader-follow ing multi-agent systems w ith measurement[J]. Journalof Systems Science and Complexity,2010,23(1):35?49.

[11]HONG Y G,CHEN G R,BUSHNELL L.Distributed observers design for leader-follow ing control of multi-agent networks[J]. Automatica,2008,44(3):846?850.

[12]SONG Qiang,CAO Jinde,YU Wenwu.Second-order leader-follow ing consensus of nonlinearmulti-agent systems via pinning control[J].Systems&Control Letters,2010,59(9): 553?562.

[13]HU Guoqiang.Robust consensus tracking of a class of second-ordermultiagentdynamic systems[J].Systems&Control Letters,2012,61(1):134?142.

[14]ZHU Wei,CHENG Daizhan.Leader-follow ing consensus of second-order agents w ith multiple time-varying delays[J]. Automatica,2010,46(12):1994?1999.

[15]JIANG Fangcui,WANG Long.Consensus seeking of high-order dynamic multi-agent systems with fixed and sw itching topologies[J].International Journal of Control,2010,83(2): 404?420.

[16]NI Wei,CHENG Daizhan.Leader-follow ing consensus of multi-agent systems under fixed and sw itching topologies[J]. Systems&Control Letters,2010,59(3/4):209?217.

[17]NIWei,XIONG Chun,YANG Jie.Leader-follow ing consensus of high-order multi-agent linear systems w ith bounded transmission channels[J].International Journal of Systems Science,2013,44(9):1711?1725.

[18]TANNER H G,PAPPAS G J,KUMAR V.Input-to-state stability on formation graphs[C]//Proceedings of the 41st IEEE Conference on Decision and Control,NJ:IEEE,2002: 2439?2444.

[19]KHALIL H K,GRIZZLE JW.Nonlinear systems[M].3rd ed. Upper Saddle River:Prentice Hall,2002:174?180.

[20]HORN R A,JOHNSON C R.Topics in matrix analysis[M]. Cambridge,UK:Cambridge University Press,1991:242?254.

(編輯 趙俊)

Consensus analysisand design prob lem for leader-follow ing linearmulti-agent system s

GEYanrong1,CHEN Yangzhou2,SONG Xuejun1,QIYaohui1

(1.College of Physics Science and Information Engineering,HebeiNormalUniversity,Shijiazhuang 050024,China; 2.College of Metropolitan Transportation,Beijing University of Technology,Beijing 100124,China)

Consensus analysis and design problem for leader-follow ing linear multi-agent system s(LLMASs)w ith directed information topology was investigated.A proper linear transformation was proposed to transform the consensus problem of a leaderwith disturbance inputs to the input-to-state stability problem of a corresponding linear system.Then, a new consensus criterion in terms of Hurwitz stability of matrices was given for LLMASs achieving consensus w ith directed information topologies,and the tracking error was estimated.Moreover,a design process to determ ine the feedback gain matrix in the consensus protocol was proposed.Finally,the consensus was extended to the formation control.Numericalexamplesaregiven to validate the above theoretical results.

multi-agent systems;leader-following consensus;input-to-state stability;consensus criterion;formation control

TP13

A

1672?7207(2017)03?0735?07

10.11817/j.issn.1672-7207.2017.03.023

2016?03?29；

2016?06?12

國家自然科學基金資助項目(61573030，61511130044)；河北省教育廳基金資助項目(ZC2016037)；河北師范大學科研基金資助項目(L2015B06,L2015B07)(Projects(61573030,61511130044)supported by the National Natural Science Foundation of China; Project(ZC2016037)supported by the Foundation of Hebei Education Departm ent;Projects(L2015B06,L2015B07)supported by the Science and Research Foundation ofHebei NormalUniversity)

宋學君，博士，教授，從事多智能體系統協作控制、多傳感器信息融合的研究；E-mail:sxj263@126.com