本科計量經(jīng)濟學“任務驅(qū)動型”教學模式的實施

田翠杰

摘 要：本科計量經(jīng)濟學“任務驅(qū)動型”教學模式，是以小、中、大型任務為核心，通過教師與學生兩大主體、三個實驗教學層次和四種教學方法，完成一個教學目標的一種教學模式。這種模式可以充分調(diào)動學生的學習興趣，使其輕松掌握計量經(jīng)濟學基本理論與模型構(gòu)建的基本方法，進而提高其解決實際問題的能力。

關(guān)鍵詞：任務驅(qū)動；實驗；模式

中圖分類號：G642 文獻標志碼：A 文章編號：2096-000X（2017）21-0117-03

Abstract： Task-driven teaching model of undergraduate econometrics takes small， medium and large tasks as the core. Students and teachers are the two major subjects. This kind of teaching model has three different teaching layers and four teaching methods. All the above factors are combined to achieve one certain teaching target. This model can fully mobilize students' interest in learning， so that they can easily grasp the basic theory of econometrics and the fundamental method of model construction， and thus improve their ability to solve practical problems.

Keywords： task-driven； experiment； model

一、計量經(jīng)濟學“任務驅(qū)動型”教學體系

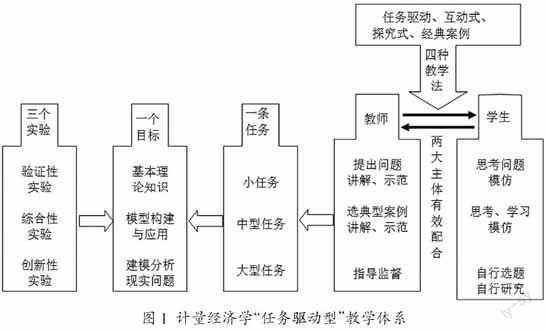
任務驅(qū)動型實驗教學模式主要是基于一些實際任務，在明確的學習目標下，啟發(fā)和鼓勵學生運用所學知識，解決現(xiàn)實問題，從而使學生學習到隱含于任務背后的知識與理論，并掌握分析問題和解決問題的方法。其教學體系，如圖1所示。

二、計量經(jīng)濟學“任務驅(qū)動型”教學模式的實施方式

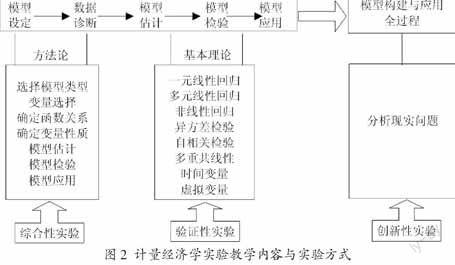
學習計量經(jīng)濟學的最終目標是應用，使其掌握模型構(gòu)建與應用的全過程，其最終實現(xiàn)方式是創(chuàng)新性實驗，但創(chuàng)新性實驗要求掌握系統(tǒng)的計量經(jīng)濟學理論知識。學生操作難度較大，在進行創(chuàng)新性實驗教學前必須掌握建模的基本理論和方法論，這就需要以驗證性實驗和綜合性實驗為基礎(chǔ)，在完成這兩者以后才可以實施。所以，結(jié)合計量經(jīng)濟學的知識體系和理論特點及建模要求，針對不同的學習內(nèi)容，必須分別采取驗證性實驗、綜合性實驗和創(chuàng)新性實驗三種實驗方式，如圖2所示。

三、計量經(jīng)濟學“任務驅(qū)動型”教學模式的具體實施

在多元線性回歸模型中，最關(guān)鍵的問題是解釋變量的選取，要保證解釋變量間相對獨立，即不存在多重共線性。因此，本教學模式首先采取驗證性實驗講解檢驗與修正多重共線性的基本理論；然后，以多元線性回歸模型的經(jīng)典案例引出綜合性實驗，重點突出對“數(shù)據(jù)診斷、模型設定與應用”等計量經(jīng)濟學建模過程和方法論的講解和實際操作；最后，以創(chuàng)新性實驗讓學生進行多元線性回歸模型構(gòu)建與應用的全過程操作，對經(jīng)濟社會的熱點問題、焦點問題進行分析。

（一）通過驗證性實驗教學使學生掌握多重共線性基本理論知識和軟件基本操作

驗證性實驗教學重點是讓學生掌握計量經(jīng)濟學的基本理論、基本方法、基本技巧和基本軟件。主要是先由教師提出與要講授的基礎(chǔ)理論知識相關(guān)的“小型”任務；然后由學生思考為完成該任務可能會遇到的問題，這些問題便是要講授的理論知識；接著，教師講授基本理論知識和軟件操作方法；最后由學生模擬教師練習軟件操作，并驗證基本理論知識。比如在多重共線性的檢驗與修正中，首先給出一個多元線性回歸模型的估計結(jié)果并提出“小型”任務——讓學生觀察估計結(jié)果存在的問題，并考慮如何解決。

已知多元線性回歸模型估計結(jié)果如下：

（-1.50） （3.83） （0.16） （-0.49） （3.64）

R2 = 0.9261，F(xiàn) = 100.25，DW = 0.47，T = 37（1978-2014），t0.025（32）= 2.04

其中，各變量的含義如下：

Y——糧食產(chǎn)量（萬噸）

X1——播種面積（千公頃）

X2——農(nóng)業(yè)勞動力（萬人）

X3——農(nóng)業(yè)機械總動力（萬千瓦）

X4——化肥施用量（萬噸）

1. 提出任務。對于這一任務，引導學生根據(jù)建模步驟得到模型結(jié)果后，要對其進行經(jīng)濟意義檢驗和統(tǒng)計檢驗，在檢驗過程中去發(fā)現(xiàn)問題。學生在完成檢驗任務后會發(fā)現(xiàn)模型存在的問題：R2 和F 值都很大，說明模型的線性擬合程度很好和總體線性關(guān)系顯著成立；而檢驗自變量X2和X3顯著性的t統(tǒng)計量卻沒有通過檢驗，X3的系數(shù)不符合經(jīng)濟意義。接著請學生思考“為什么會出現(xiàn)這樣的問題？應該如何解決？”總體線性關(guān)系成立說明各個自變量聯(lián)合起來對因變量的解釋能力強，而又有某個自變量的解釋能力不強，說明很難區(qū)分每個自變量對因變量的解釋能力，這應該是由于自變量間的相關(guān)性很強，才使得它們的作用難以區(qū)分，并容易導致回歸系數(shù)不符合經(jīng)濟意義。那么這種現(xiàn)象就叫做多重共線性，而我們發(fā)現(xiàn)問題的這一過程就是檢驗多重共線性的方法。

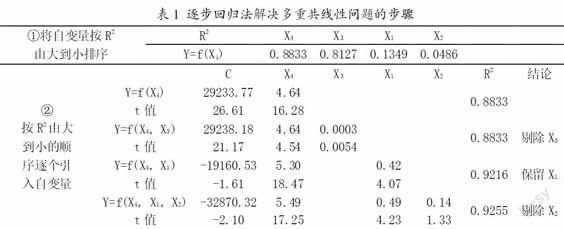
2. 解決問題，完成任務。下一步就是要引導學生考慮如何解決這一問題，既然自變量之間相關(guān)性較強，那么就可以只保留一部分自變量，關(guān)鍵問題是保留哪些？剔除哪些自變量呢？總體思路肯定是要保留解釋能力強的自變量，那么就要對各個自變量的解釋能力進行排序。因此，用因變量與每個自變量進行回歸，按照回歸方程R2的大小進行排序，就是按照自變量的解釋能力由大到小排序，先用R2最大的自變量對因變量進行回歸，在此基礎(chǔ)上引入R2其次大的自變量，引入后如果R2變大，且兩個自變量的t統(tǒng)計量都通過檢驗，則兩個自變量都保留，如果R2變小，則不引入R2其次大的自變量，直接引入R2排第3的自變量，依據(jù)R2和t值的變化判斷是否保留第3個自變量；以此類推，逐個引入其余自變量，最后可以確定最終需要保留的自變量，從而避免多重共線性。這一方法就是解決多重共線性問題的逐步回歸法。以上述例題為例，逐步回歸法的具體過程如表1所示，最終結(jié)果是保留X4和X1。

（二）通過綜合性實驗教學使學生掌握構(gòu)建模型的方法論

綜合性實驗教學注重培養(yǎng)學生的拓展能力，重點在于讓學生在掌握基本理論、基本方法的基礎(chǔ)上，通過閱讀相關(guān)的文獻和經(jīng)典案例，學習計量經(jīng)濟學的基本分析范式，掌握構(gòu)建與分析計量經(jīng)濟模型的能力。仍然是先由教師提出一個能貫穿整個理論知識體系的“中型”任務；然后由學生思考如何去完成該任務；接著，教師分步驟講授模型的構(gòu)建與分析；最后由學生模擬教師練習計量經(jīng)濟學建模的全過程。

在本套實驗教學體系中，該模式仍采用教師操作、學生模仿的教學形式，重點突出對“理論模型構(gòu)建、模型應用”等計量經(jīng)濟學建模全過程的講解和實際操作，讓學生對理論知識體系融會貫通，并掌握實驗軟件的系統(tǒng)操作。

比如，由教師提出一個“中型”任務：分析第二產(chǎn)業(yè)增加值的影響因素，讓學生思考如何完成。教師可以引導學生依據(jù)生產(chǎn)函數(shù)理論選擇“第二產(chǎn)業(yè)增加值”作為因變量，選擇“第二產(chǎn)業(yè)固定資產(chǎn)投資”、“第二產(chǎn)業(yè)從業(yè)人員”作為自變量，為了練習多重共線性還可以加入“第二產(chǎn)業(yè)R&D投入”作為自變量；然后由教師引導學生如何利用這些變量建立模型、估計模型并分析和解決模型的多重共線性問題。

（三）通過創(chuàng)新性實驗教學使學生掌握模型構(gòu)建與應用的全過程

創(chuàng)新性實驗教學模式采用教師引導、學生操作的教學形式。首先由教師提出一個“大型”任務——用計量經(jīng)濟模型分析經(jīng)濟社會的熱點、焦點問題；然后由學生結(jié)合專業(yè)背景，自行選擇要研究的問題，自行設計研究方案、收集數(shù)據(jù)、撰寫報告；最后由教師組織答辯、反饋意見，讓學生熟練掌握計量經(jīng)濟學模型的建模全過程與實驗軟件的操作。比如，老師讓學生自選一個現(xiàn)實問題，結(jié)合經(jīng)濟學理論建立多元線性回歸模型，并分析和解決模型的多重共線性問題。

參考文獻：

[1]謝家泉.基于科教融合理念的計量經(jīng)濟學教學模塊設計與應用[J].高教學刊，2016（22）：79-80.

[2]支小軍，劉永萍.計量經(jīng)濟學“三位一體”實驗教學模式的探索與實踐[J].吉林省教育學院學報，2013（5）：27-28.

[3]劉曉平.《計量經(jīng)濟學》探索性實驗教學模式研究——以青海大學為例[J].科教導刊，2011（11）：114-115.

[4]莫旋，何青.計量經(jīng)濟學理論與實踐教學相融合教學模式探討[J].現(xiàn)代商貿(mào)工業(yè)，2016（29）：207-208.

[5]李廣析，孔蔭瑩.淺析計量經(jīng)濟學課程建設和教學改革[J].高教學刊，2016（15）：72-73.